In-Depth
Functional Programming, the .NET Way, Part 2
We looked at the basic features of functional programming with Visual F#. In this second part, we take it a bit farther and look at creating anonymous functions, pattern matching, and other features of F#.
- By Arnaldo Pérez Castaño
- 02/16/2016
Also See:
Last time, we examined the advantages, benefits of programming using the functional paradigm, specifically, programming with Microsoft's Visual F#. I explained some of the syntactic sugars that allow .NET developers to be able to code with F# without having to rethink the development process, yet maintain clean, compact, elegant and expressive code.
This time I'll take a look at the variety of functions and features that F# offers developers who want to take advantage of the functional programming paradigm. I'll start with anonymous functions.
Anonymous Functions
Anonymous functions are sometimes referred as lambda functions because of their similarity. They try to simplify the definition of functions by eliminating the need to set a name to defined functions. It could be useful for creating simple functions that we would require to support calculations in an outer function. To create an anonymous function we use keywords fun or function. The latter allow us to use pattern matching, which I'll describe later in this article. Here is a sample, with the result in Figure 1:
// f(n) = 2*n + 3*n
let f n =
let double = (fun x -> x*2) n
let triple = (fun x ->> x*3) n
double + triple
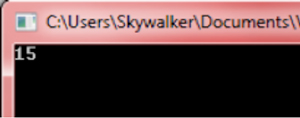
printfn "%A" (factorial 4)
 [Click on image for larger view.]
Figure 1: Result of a Simple Anonymous Function
[Click on image for larger view.]
Figure 1: Result of a Simple Anonymous Function
In the previous function we calculated the 2*n value by creating a quick anonymous function and evaluating it, and we proceed analogously in order to obtain the 3*n value.
Recursion
A function is considered recursive when it's defined in terms of itself; that is, the function calls itself within its definition. Solutions to diverse problems could be expressed recursively. The recursive solution is usually the most legible and elegant, and in pure functional programming any loop is achieved by means of recursive functions. Consequently, recursion constitutes an indispensable technique for functional programmers. As F# is mainly a functional language we prefer to iterate recursively even though there exists the possibility of iterating using procedural statements like the "for" statement.
To use recursion in F#, we use the let keyword followed by the rec keyword, that's how we tell the compiler that the identifier (function name) should be available within the function definition. In the next code we present the factorial function, this time created in F#:
let rec factorial n =
if n <= 1 then
1
else
n * factorial (n - 1)
In the next section we'll examine a technique known as pattern matching. Common in functional languages, it will make our recursion more elegant and expressive.
Pattern Matching
Similar to if...else if ... else block statements or to a switch statement in C#, pattern matching allows you to make different computations depending on the value of an identifier. This construct gives you the possibility of pattern match over different values and types, in the next example we implement the Fibonacci function (computes the nth element in the Fibonacci sequence) using recursion and pattern matching:
let rec fibonacci x =
match x with
| 1 -> 1
| 2 -> 1
| x -> fibonacci (x-1) + fibonacci (x-2)
How does it work? The construct starts with the match keyword followed by the value we want to match, in this case x, it's followed by the "with" keyword and then divided by | all possible matches as pairs m -> n where m represents a value of x to be matched and n the value returned in case x = m. The first match found will be the result of the pattern matching expression. In the particular case of the Fibonacci function it occurs that when x = 1 the result is 1, when x = 2 the result is 1 otherwise the result is Fibonacci(x-1) + Fibonacci(x-2).
Curried Functions
The term currying, sometimes mentioned as partial application, refers to the possibility of having a function f1 that expects n arguments to receive the first argument and then return a function f2, then pass the second argument to f2 and obtain another function f3, continuing this process until the last argument has been passed to the function fn. Hence, curried functions allow us to pass a number of arguments and always get a residual function expecting the remaining arguments:
let f x y = x ** 2.0 + y
// Pass first argument
let g = f 3.0
// Pass second argument
let h = g 1.0
In the previous example function f(x, y) = x^2 + y is partially applied by passing argument x = 3 and putting the result in function g(y) = 3^2 + y = 9 + y. The final result and complete application of f lies in h after having provided the last argument.
Pipeline Operator
The Pipeline operator (|>), give us the possibility of chaining functions all together. Or, to be more precise, it allows us to create a chain f1 |> f2 |> f3 |>> ... |> fn where each function operates on the result of the previous -- that is, f2 operates on the result of f1, f3 on the result of f2 and so on:
let f1 s = s
let f2 s = s + "Jordan"
let f3 s = s + "23!"
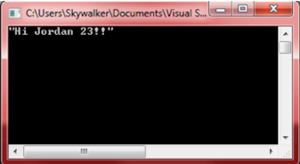
let l = f1 "Hi" |> f2 |> f3
printfn "%A" l
 [Click on image for larger view.]
Figure 2: Pipeline Operator Strings the Results Together
[Click on image for larger view.]
Figure 2: Pipeline Operator Strings the Results Together
This operator comes in handy for creating compact functions like the one from the above code which concatenates a set of strings to create a simple message (see Figure 2). The pipeline operator can save a lot of time and effort and we'll see more of it in the next section.
Higher Order Functions
As it was previously mentioned functions in F# are treated as first class citizens. They can be stored as values, returned as the result of some expression and submitted as arguments to another function. This last characteristic defines a higher order function, i.e., a function that accepts another function as an argument. Higher order functions are useful in scientific and academic environments where the use of numerical algorithms, numerical math, optimization, etc. calls the need for this type of expressivity. Let's examine some of the popular higher order functions present in F#, all related to collections:
Map and iter -- These functions apply a given function to every item in the collection:
let l = [1;2;3]
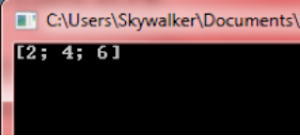
let mapped = l |> List.map(fun x -> x*2)
printfn "%A" mapped
 [Click on image for larger view.]
Figure 3: Result of High Order Function
[Click on image for larger view.]
Figure 3: Result of High Order Function
Fold -- Applies a function to every item in the collection folding the results into an accumulator which is later returned. The second argument of the fold function determines the initial value of the accumulator; in the next example, it was set to 0:
let l = [1;2;3]
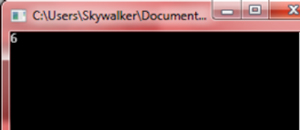
let folded = l |> List.fold (fun acc x -> acc + x) 0
printfn "%A" fold
 [Click on image for larger view.]
Figure 4: Accumulated Result
[Click on image for larger view.]
Figure 4: Accumulated Result
Filter -- This function allows you to filter elements of the collection based on a given predicate or condition:
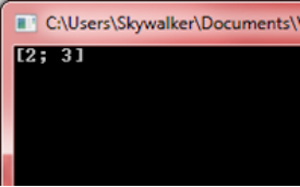
let l = [1;2;3]
let filter = l |> List.filter (fun x -> x > 1)
printfn "%A" filter
 [Click on image for larger view.]
Figure 5: Filtered Result
[Click on image for larger view.]
Figure 5: Filtered Result
Exists -- Allows you to determine if there are elements in the collection that satisfy certain criteria:
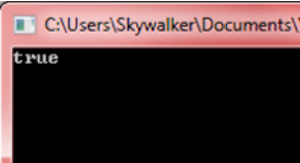
let l = [1;2;3]
let exists = l |> List.exists (fun x -> x > 1)
printfn "%A" exists
 [Click on image for larger view.]
Figure 6: Does It Exist in the Collection? Only Exists Knows
[Click on image for larger view.]
Figure 6: Does It Exist in the Collection? Only Exists Knows
Similar higher order functions to the ones listed above exist and they can provide clean, simple solutions to different situations that you might encounter. Here we presented just some of the basics.
In this article we have described, in an introductory manner, some of the features of the functional paradigm. We have examined F# as a mainly functional programming language and we have analyzed some of the relevant topics that it includes.
I hope that after reading this article the reader can now understand the advantages of the clean, compact, elegant and expressive code offered by functional languages, as well as the advantages of many of its characteristics.
About the Author
Arnaldo Perez Castano is a computer scientist based in Cuba. He is the author of a series of programming books -- JavaScript Facil, HTML y CSS Facil, and Python Facil (Marcombo S.A). His expertise includes Visual Basic, C#, .NET Framework, and artificial intelligence, and offers his services as a freelancer through nubelo.com. Cinema and music are some of his passions. Contact him at [email protected].