Neural Network Lab
Understanding and Using K-Fold Cross-Validation for Neural Networks
James McCaffrey walks you through whys and hows of using k-fold cross-validation to gauge the quality of your neural network values.
Cross-validation is a process that can be used to estimate the quality of a neural network. When applied to several neural networks with different free parameter values (such as the number of hidden nodes, back-propagation learning rate, and so on), the results of cross-validation can be used to select the best set of parameter values.
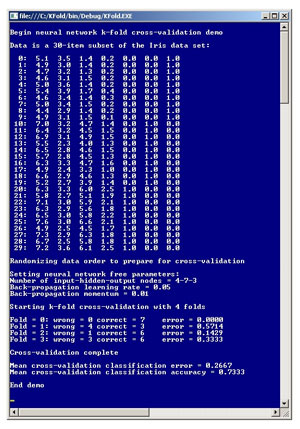
While there are several types of cross-validation, this article describes k-fold cross-validation. The best way to get a feel for how k-fold cross-validation can be used with neural networks is to take a look at the screenshot of a demo program in Figure 1.
 [Click on image for larger view.]
Figure 1. K-Fold Cross-Validation Demo
[Click on image for larger view.]
Figure 1. K-Fold Cross-Validation Demo
The demo begins by setting up and displaying a 30-item data set. Each data item has four x-values followed by three y-values that encode a species of iris flower. The data is a subset of a well-known 150-item machine learning data set called Fisher's Iris data. The four x-values are sepal length, sepal width, petal length and petal width. There are three possible species: Iris setosa is encoded as (0,0,1), Iris versicolor is encoded as (0,1,0) and Iris virginica is encoded as (1,0,0). The overall problem is to predict the species of an iris flower from x-values.
The demo begins by randomizing the order of the data set. Next the demo sets the values of the free parameters of the neural network to be evaluated. The number of input, hidden and output nodes are 4, 7 and 3, respectively. The neural network uses back-propagation for training. Back-propagation requires a learning rate, set to 0.05, and in this case a momentum value, set to 0.01.
The demo uses four folds. The most common value for number of folds is 10, but the demo uses just four folds for simplicity. The k-fold cross-validation process yields a measure of quality for each fold. Here the measure of quality is classification error which is a percentage of incorrectly classified flowers, so smaller values are better. Behind the scenes, the demo uses an artificially small number of training iterations so that there isn't 100 percent accuracy in each fold. In the first fold of data, the neural network correctly classified all data items. In the last fold, the neural network correctly classified six out of nine items. The demo concludes by displaying the average classification error (eight out of 30 incorrect = 0.2667) and the equivalent average classification accuracy (22 out of 30 correct = 0.7333).
Before we get further into this topic, please note that this article assumes you have at least intermediate-level developer skills but does not assume you know anything about cross-validation. Although a basic knowledge of neural networks would be helpful, you should be able to understand this article even if you are new to neural networks. I coded the demo program in C# but you should have no trouble refactoring the demo to any language that has support for the object oriented programming paradigm. The source code for the demo program is too long to present in its entirety in this article, but the complete demo is available as a code download -- simply click on the code download button at the top of this page. I removed most error-checking code to keep the main ideas as clear as possible.
Understanding Cross-Validation
The mechanics of cross-validation are relatively simple, but the reasons why cross-validation is used with neural networks are a bit subtle. The ultimate goal of the classification problem shown in Figure 1 is to find a set of neural network weights and bias values so that the input data generates output values that best match the target values. A simplistic approach would be to use all of the available 30 data items to train the neural network. However, this approach would likely find weights and bias values that match the data extremely well -- in fact, probably with 100 percent accuracy -- but when presented with a new, previously unseen set of input data, the neural network would likely predict very poorly. This phenomenon is called over-fitting. To avoid over-fitting, the idea is to separate the available data into a training data set (typically 80 percent to 90 percent of the data) that's used to find a set of good weights and bias values, and a test set (the remaining 10 percent to 20 percent of the data) that is used to evaluate the quality of resulting neural network.
The simplest form of cross-validation randomly separates the available data into a single training set and a single test set. This is called hold-out validation. But the hold-out approach is somewhat risky because an unlucky split of the available data could lead to an ineffective neural network. One possibility is to repeat hold-out validation several times. This is called repeated sub-sampling validation. But this approach also entails some risk because, although unlikely, some data items could be used only for training and never for testing, or vice versa.
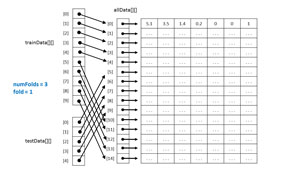
The idea behind k-fold cross-validation is to divide all the available data items into roughly equal-sized sets. Each set is used exactly once as the test set while the remaining data is used as the training set. Take a look at the image in Figure 2 . The matrix (implemented as an array of arrays) labeled allData has 15 data items. The number of folds has been set to three. Each subset of data has 15/3 = 5 items. So subset [0] data ranges from indices [0] to [4], subset [1] ranges from indices [5] to [9], and subset [2] ranges from [10] to [14].
 [Click on image for larger view.]
Figure 2. K-Fold Training and Test Data
[Click on image for larger view.]
Figure 2. K-Fold Training and Test Data
The k-fold cross-validation process iterates over the number of folds. For fold k=0, the five-item test set would be data items [0] through [4], and the 10-item training set would be data items [5] through [14]. For fold k=1, (the scenario in Figure 2), the test set would be data items [5] through [9] and the training set would be data items [0] through [4] and also [10] though [14]. For fold k=2, the test set would be items [10] trough [14] and the training set would be items [0] through [9].
In Figure 2, notice that for efficiency the training and test data sets are implemented as references to the data source in memory, rather than duplicating the data values. Also, the example here is fortunate because the number of folds (3) divides evenly into the number of available data items (15). In situations where the number of folds doesn't divide evenly, the last data subset picks up the extra data items. For example, in Figure 2, if the number of folds had been set to four, the first three subsets would contain 15/4 = 3 data items and the last subset would contain the remaining six data items.
Overall Program Structure
To create the k-fold cross-validation demo, I launched Visual Studio and created a new C# console application named KFold. The demo has no significant dependencies and so any version of Visual Studio will work. In the Solution Explorer window I renamed file Program.cs to the more-descriptive KFoldProgram.cs and VS automatically renamed associated Program class.
The overall structure of the program, with most WriteLine statements removed and a few minor edits, is presented in Listing 1, below. For simplicity, I hardcoded the 30-item data set. In most situations you'll be reading from a text file or fetching from a SQL database. The demo begins by randomizing the order of the allData matrix:
RandomizeOrder(allData);
This is important because the raw data is ordered by y-values (the encoded Iris species), so if the order isn't randomized in each fold, the test data set would be dominated by one encoded species. Method RandomizeOrder uses the Fisher-Yates shuffle algorithm and is defined as:
static void RandomizeOrder(double[][] allData)
{
Random rnd = new Random(0);
for (int i = 0; i < alldata.length;="" ++i)="" {="" int="" r="rnd.Next(i," alldata.length);="" double[]="" tmp="allData[r];" alldata[r]="allData[i];" alldata[i]="tmp;" }="">
For simplicity, the demo program doesn't normalize the numeric data. Because the raw x-values are all in more or less the same range, not normalizing is acceptable, but in many problem scenarios you'll want to normalize numeric input data.
Listing 1: Cross-Validation Demo Program Structure
using System;
namespace KFold
{
class KFoldProgram
{
static void Main(string[] args)
{
Console.WriteLine("\nBegin neural network k-fold cross-validation demo\n");
double[][] allData = new double[30][];
allData[0] = new double[] { 5.1, 3.5, 1.4, 0.2, 0, 0, 1 };
allData[1] = new double[] { 4.9, 3.0, 1.4, 0.2, 0, 0, 1 };
// Etc.
allData[29] = new double[] { 7.2, 3.6, 6.1, 2.5, 1, 0, 0 };
Console.WriteLine("Data is a 30-item subset of the Iris data set:\n");
ShowMatrix(allData, allData.Length, 1, true, true);
RandomizeOrder(allData);
int[] numNodes = new int[] { 4, 7, 3 };
double learnRate = 0.05;
double momentum = 0.01;
int numFolds = 4;
double mce = CrossValidate(numNodes, allData, numFolds, learnRate, momentum);
double mca = 1.0 - mce;
Console.WriteLine("Mean cross-validation classification error = " +
mce.ToString("F4"));
Console.WriteLine("Mean cross-validation classification accuracy = " +
mca.ToString("F4"));
Console.WriteLine("\nEnd demo\n");
} // Main
static void RandomizeOrder(double[][] allData) { . . }
static double CrossValidate(int[] numNodes, double[][] allData, int numFolds,
double learnRate, double momentum) { . . }
static double[][] GetTrainData(double[][] allData, int numFolds, int fold) { . . }
static double[][] GetTestData(double[][] allData, int numFolds, int fold) { . . }
static int[][] GetFirstLastTest(int numDataItems, int numFolds) { . . }
// Several utility methods here
} // Program
public class NeuralNetwork
{
// Fields here
public NeuralNetwork(int numInput, int numHidden, int numOutput) { . . }
public void SetWeights(double[] weights) { . . }
public void InitializeWeights(int seed) { . . }
public double[] GetWeights() { . . }
public double[] Train(double[][] trainData, int maxEpochs,
double learnRate, double momentum) { . . }
public double Accuracy(double[][] testData) { . . }
public int[] WrongCorrect(double[][] testData) { . . }
// Private methods here
}
} // ns
The heart of the demo is a call to method CrossValidate. The call to CrossValidate is prepared like so:
int[] numNodes = new int[] { 4, 7, 3 }; // Input, hidden, output
double learnRate = 0.05;
double momentum = 0.01;
int numFolds = 4;
The CrossValidate method accepts the number of nodes for the neural network, the back-propagation learning rate and momentum value, the number of folds to use and a reference to the data items. If you were using a neural network that used a different training algorithm, such as particle swarm optimization, you would have to modify method CrossValidate to accept the appropriate parameters.
The demo calls method CrossValidate like this:
double mce = CrossValidate(numNodes, allData, numFolds,
learnRate, momentum);
double mca = 1.0 - mce;
Console.WriteLine("Mean cross-validation classification error = " +
mce.ToString("F4"));
Console.WriteLine("Mean cross-validation classification accuracy = " +
mca.ToString("F4"));
CrossValidate returns the average classification error over the k folds. In machine learning, it's more common to use error, rather than accuracy, but I prefer to see both error and accuracy values.
The Cross-Validation Method
The code for Method CrossValidate is presented in Listing 2.
Listing 2: Method CrossValidate
static double CrossValidate(int[] numNodes, double[][] allData,
int numFolds, double learnRate, double momentum)
{
int[] cumWrongCorrect = new int[2];
for (int k = 0; k < numfolds;="" ++k)="" each="" fold="" {="" neuralnetwork="" nn="new" neuralnetwork(numnodes[0],="" numnodes[1],="" numnodes[2]);="" nn.initializeweights(0);="" don't="" forget="" this!="" double[][]="" traindata="GetTrainData(allData," numfolds,="" k);="" double[][]="" testdata="GetTestData(allData," numfolds,="" k);="" double[]="" bestweights="nn.Train(trainData," 35,="" learnrate,="" momentum);="" nn.setweights(bestweights);="" not="" really="" necessary="" with="" back-prop="" int[]="" wrongcorrect="nn.WrongCorrect(testData);" compute="" classification="" results="" double="" error="(wrongCorrect[0]" *="" 1.0)="" (wrongcorrect[0]="" +="" wrongcorrect[1]);="" cumwrongcorrect[0]="" +="wrongCorrect[0];" cumwrongcorrect[1]="" +="wrongCorrect[1];" accumulate="" the="" classification="" results="" console.write("fold=" + k + " :="" wrong=" + wrongCorrect[0] +
" correct=" + wrongCorrect[1]);
Console.WriteLine(" error=" + error.ToString(" f4"));="" }="" return="" (cumwrongcorrect[0]="" *="" 1.0)="" (cumwrongcorrect[0]="" +="" cumwrongcorrect[1]);="">
In high-level pseudo-code, method CrossValidate is:
for each fold k
instantiate a neural network
get reference to training data for k
get reference to test data for k
train the neural network
accumulate number wrong, correct
end for
return number (total wrong) / (wrong + correct)
So, the keys to k-fold cross-validation are really the two methods which return references to the test and training data. Method GetTestData is the simpler of the two. That method is implemented like this:
static double[][] GetTestData(double[][] allData, int numFolds, int fold)
{
int[][] firstAndLastTest = GetFirstLastTest(allData.Length, numFolds);
int numTest = firstAndLastTest[fold][1] - firstAndLastTest[fold][0] + 1;
double[][] result = new double[numTest][];
int ia = firstAndLastTest[fold][0]; // Index into all data
for (int i = 0; i < result.length;="" ++i)="" {="" result[i]="allData[ia];" the="" test="" data="" indices="" are="" contiguous="" ++ia;="" }="" return="" result;="">
If you refer to Figure 2, found earlier in this article, you'll notice that the first and last indices of the test data depend on the number of folds and the value of the current fold. Those two indices are determined by helper method GetFirstLastTest, which is presented in Listing 3. The method returns an array of arrays where the first index is the fold value, and the two int values are the first and last indices. For example, if the method is called on the data shown in Figure 2 with15 items and numFolds = 3, and the results are returned into int[][] indices, then indices[1][0] is the first test index for fold = 1, which is five, and indices[1][1] is the last test index for fold = 1, which is nine.
Listing 3: Method GetFirstLastTest
static int[][] GetFirstLastTest(int numDataItems, int numFolds)
{
int interval = numDataItems / numFolds;
int[][] result = new int[numFolds][];
for (int i = 0; i < result.length;="" ++i)="" result[i]="new" int[2];="" for="" (int="" k="0;" k="">< numfolds;="" ++k)="" {="" int="" first="k" *="" interval;="" int="" last="(k+1)" *="" interval="" -="" 1;="" result[k][0]="first;" result[k][1]="last;" }="" result[numfolds-1][1]="result[numFolds-1][1]" +="" numdataitems="" %="" numfolds;="" return="" result;="">
If you trace though an example or two, you should be able to see how helper method GetFirstLastTest works. The next-to-last statement containing the modulus operator takes into account any leftover data items in situations where the number of available data items is not evenly divisible by the number of folds.
Method GetTrainData is a bit trickier than GetTestData because the test indices will be contiguous, but the training indices may be non-sequential. Method GetTrainData is presented in Listing 4.
Listing 4: Method GetTrainData
static double[][] GetTrainData(double[][] allData, int numFolds, int fold)
{
int[][] firstAndLastTest = GetFirstLastTest(allData.Length, numFolds);
int numTrain = allData.Length -
(firstAndLastTest[fold][1] - firstAndLastTest[fold][0] + 1);
double[][] result = new double[numTrain][];
int i = 0; // Index into result/test data
int ia = 0; // Index into all data
while (i < result.length)="" {="" if="" (ia="">< firstandlasttest[fold][0]="" ||="" ia=""> firstAndLastTest[fold][1]) // This is a TRAIN row
{
result[i] = allData[ia];
++i;
}
++ia;
}
return result;
}
To summarize, method CrossValidate calls helper methods GetTestData and GetTrainData. Each of these two helper methods calls helper method GetFirstLastTest, which returns the first and last indices for the designated test data, for all folds.
Alternatives and Comments
Cross-validation is essentially a technique to gauge the quality of a particular neural network. Knowing the quality of a neural network allows you to identify when over-fitting has occurred. In most cases you will run cross-validation many times on a neural network, using different values of the free parameters -- the number of hidden nodes and parameters related to the training algorithm, such as the learning rate and the momentum value for back-propagation. In neural network terminology this is often called a parameter sweep. You can keep track of which set of free parameter values yields the best neural network; that is, the set which has the lowest error rate. This avoids over-fitting. With the best free parameter values in hand, you can then train your neural network using all available data. The associated k-fold cross-entropy mean error rate is the estimated error rate of your final neural network.
Note that for simplicity, the demo presented in this article uses four folds. There is some research that suggests k=10 is a reasonable number of folds to use in most situations. More folds yields a more accurate estimate of classification error at the expense of time. An extreme approach is to set the number of folds equal to the number of available data items. This will result in exactly one data item being a test item during each fold iteration. This technique is called leave-one-out (LOO) cross-validation.
The version of k-fold cross-validation presented in this article uses simple classification error -- the number of wrong classifications on the test data divided by the total number of test items -- as the measure of quality. There is some research that suggests an alternative measure called cross-entropy error is superior to simple classification error. Using cross-entropy error is a relatively advanced topic and will be examined in a future article.