On VB
When Hexadecimal is Just Not Enough
Joe Kunk looks at how to manage a numeric system that extends to the entire alphabet.
One of the things I really enjoy is taking a familiar concept and seeing just how far I can push it. It is one of those boyhood traits that I have never outgrown. Like the time that I discovered that ice-fishing with a gas lantern in a well-ventilated and well-insulated ice-fishing shanty would keep the seating area comfortably t-shirt warm for hours. Add a portable music player and a thermos full of my favorite beverage and I had one mighty fine ice-fishing experience. Did I mention that I don't eat fish?
As a computer science student at Michigan State University, I was quickly taught the binary, octal, and hexadecimal number systems. As we know, hexadecimal is the base 16 numeric system and is represented by the standard 0-9 numeric sequence, extended by the letters A-F to provide the needed 16 digits. I remember wondering why they stopped at F and didn't go all the way to Z. We know that the reason is because each hexadecimal digit can be represented in exactly 4 bits and that aligns well with the word boundaries of most if not all computer systems.
A colleague asked for my advice recently on how to satisfy a challenging business requirement. He needed the ability to store a lot of large numbers into a handheld device that had limited memory and may not be synchronized with a computer for up to 24 hours at a time. Bar codes could be used, but the device user must also enter the number from the barcode into the handheld to verify that it read correctly, since the processes used on the material could damage the barcode and cause it to misread. The handheld device has a full alphanumeric keyboard.
Alphadecimal as a Numeric Representation
You may have already guessed my recommendation. Why not represent the numbers in base 36, using the digits 0-9 extended by the letters A-Z. I called it "alphadecimal" since it uses the full alphabet. Just as I was feeling clever, I typed "alphadecimal" into the Bing search engine and it brought up an article on Base 36 in Wikipedia; so much for coining a new term. That article indicates that the Service Tag on Dell computers is a five or seven digit alphadecimal number and that the URL shortening service TinyURL makes use of alphadecimal as well. Alphadecimal has the advantage of being shorter and easier to type for larger numbers.
For utilizing alphadecimal, the programming task consists primarily of a pair of conversion routines between decimal and alphadecimal. Any needed mathematical functions for alphadecimal can be performed by converting the operands to decimal, performing the operation, and converting the result back to alphadecimal.
I have prepared a Visual Studio 2010 Windows Forms demo application written in Visual Basic that converts between decimal and alphadecimal values, which you can download using the Download link at the top of this article. The demo screen is shown in Figure 1. You can enter a decimal number on the left and click the "To Alphadecimal" button to convert the value to alphadecimal or the reverse by entering an alphadecimal figure on the right and clicking "To Decimal".
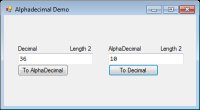
[Click on image for larger view.] |
| Figure 1.The Alphadecimal Demo screen. |
You see that under Base 36, "10" is the same as the numeric base or radix value, just as "10" results in the decimal value 16 in hexadecimal notation. I used the Consolas font to provide a high visual contrast between zeros and the letter "O" in the displayed values.
Figure 2 shows the maximum 64-bit integer that can be represented by the demo application and its equivalent alphadecimal value. You can produce this number by double-clicking the Decimal textbox in the demo application. You see that Base 36 notation requires 6 digits less to represent this figure than decimal notation requires, with the added benefit of alphadecimal being much easier to write or type than the decimal figure.
Coding the AlphaDecimal class
Following recommended practice, I created a class project AlphaDecimal that contains the main process logic, leaving the Windows form class to solely manage the screen interactions. Each of the functions are implemented as Shared methods making access to them easier by eliminating the need to instantiate the AlphaDecimal class. I set Option Explicit to On and Option Strict to On for the AlphaDecimal project.
The class level variable AlphaDecimalCharacters defines the actual digits and exact sequence of the digits comprising the alphadecimal notation. The numeric base or radix is defined as a constant of long integer 36. See Listing 1.
'Defines the digit sequence for the alphadecimal numbering
Public Shared AlphaDecimalCharacters As Char() = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ".ToCharArray
Public Const Radix As Long = 36
The single Decode method returns the long integer equivalent of the supplied alphadecimal value. It supports negative numbers and will ignore dollar signs, commas and plus sign characters. The heavily commented routine shows how the numeric value is computed based on the digit character and its position within the AlphaDecimalCharacters string as a character array. The core logic of the Decode routine is shown in Listing 2.
'Decode one digit at a time from left to right
For i As Integer = 0 To AlphaDecimalValue.Length - 1
'Get the digit
Dim Digit As Char = Convert.ToChar(AlphaDecimalValue.Substring(i, 1))
'Determine which position it is in the array defined at top of class
Dim index As Integer = Array.IndexOf(AlphaDecimalCharacters, Digit)
'The leftmost digit of the value is string positon 0
'PlaceValue is its proper "power of 36" value based on its position
Dim PlaceValue As Long = AlphaDecimalValue.Length - i - 1
'Numeric value of the digits is its position in AlphaDecimalCharcters array
'times 36 raised to the PlaceValue power.
Dim DigitValue As Long = Convert.ToInt64(index * (Radix ^ PlaceValue))
'Add its numeric value to the accumulated total
ReturnValue += DigitValue
Next
The overloaded AlphaDecimal.Encode method takes a number of parameter value formats including string and all supported 16-bit, 32-bit, and 64-bit values. The overload for 64-bit signed long is the location of the actual encoding logic. The core logic of the Encode routine is shown in Listing 3.
If (DecimalValue < Radix) Then
ResultValue = AlphaDecimalCharacters(Convert.ToInt32(DecimalValue))
Else
While (DecimalValue <> 0)
Dim Remainder = DecimalValue Mod Radix
ResultValue = AlphaDecimalCharacters(Convert.ToInt32(Remainder)) & ResultValue
DecimalValue = Convert.ToInt64(Math.Truncate(DecimalValue / Radix))
End While
End If
Extending the Alphadecimal Concept
I introduced alphadecimal as a logical extension of the usefulness of the hexadecimal notation, taking base 16 up to base 36. Is that the end of the road, or are there still interesting ways to extend the concept in new directions? Actually, base 36 is just the beginning of the fun we can have.
Base 36 utilizes just the uppercase letters of the alphabet. There is nothing preventing us from using the lowercase letters as well, creating a base 36 + 26 = base 62. Is that the limit? No, the only real limit is the total number of the characters that can be guaranteed to be on the keyboard of each user and can be reliably distinguished when printed for the user. Depending on your preferences, that could add an additional 20 characters for a base 82 notation. I admit that may be taking it a bit extreme, but it certainly can be done.
You may have noticed that in Listing 1, the digits used in the notation and their order are explicitly defined by the AlphaDecimalCharacters string. Is there any requirement that the digits be in this particular sequence? With the algorithm used in the demo application, they could be in any sequence. Thus, if so inclined, you could define the character "1" to be the 10th digit in the numeric sequence, for example. In effect, you are scrambling the digits so that numerical sequences would make no logic sense to the casual observer. Think of it as the 21st century version of a child's secret decoder ring. Direct character mappings are relatively easy to decipher, but it could still be a very easy and useful numeric obfuscation technique.
Conclusion
I hope you found the concept of alphadecimal both interesting and useful. We saw how an understanding of numeric base notation could be used to represent decimal numbers in new ways.
I finish with a word of caution. One of the side-effects of using a numerical representation that utilizes the full alphabet is that certain numeric values form English words when encoded. If you are using alphadecimal numbering in a production application, there are certain decimal values that you may want to avoid using. I will leave the exercise of determining the alphadecimal value for the decimal numbers 739172, 1329077, 23508730562, and 44250925282014 to the reader as an illustration.