Neural Network Lab
Learning to Use Genetic Algorithms and Evolutionary Optimization
Evolutionary optimization (EO) is a type of genetic algorithm that can help minimize the error between computed output values and training data target output values. Use this demo program to learn to the method.
Evolutionary optimization (EO) is a technique for finding approximate solutions to difficult or impossible numeric optimization problems. In particular, EO can be used to train a neural network. EO is loosely based on biological chromosomes and genes, and reproductive mechanisms including selection, chromosome crossover and gene mutation. EO is really a type of genetic algorithm (GA) and implementations of the EO technique are sometimes called real-valued genetic algorithms, or just genetic algorithms.
A neural network is essentially a complex function that accepts numeric inputs and generates numeric outputs. A fully connected neural network with m inputs, h hidden nodes and n outputs has (m * h) + (h * n) + (h + n) weights and biases. Training a neural network is the process of finding values for the weights and biases so that, for a given set of training data with known input and output values, the computed outputs of the network closely match the known outputs. In other words, training a neural network is a numerical optimization problem where the goal is to minimize the error between computed output values and training data target output values.
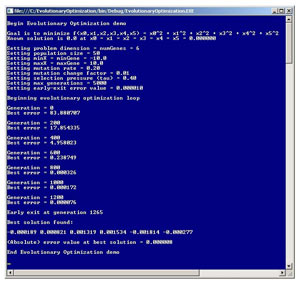
Among my colleagues, the three most common approaches for training a neural network are using the back-propagation algorithm, using particle swarm optimization, and using evolutionary optimization. In order to use EO to train a neural network you must have a solid grasp of exactly how EO works. Because neural networks are fairly complicated systems, in my opinion it's best to learn about EO by examining a simpler problem than training a neural network. Take a look at the screenshot of a demo program in Figure 1.
 [Click on image for larger view.]
Figure 1. Evolutionary Optimization Demo Program
[Click on image for larger view.]
Figure 1. Evolutionary Optimization Demo Program
The demo program uses EO to find an approximate solution to the dummy problem of identifying the values of x0, x1, x2, x3, x4, and x5 so that the function f(x0,x1,x2,x3,x4,x5)= x0^2 + x1^2 + x2^2 + x3^2 + x4^2 + x5^2 is minimized. This minimization optimization problem has an exact solution of x0 = x1 = x2 = x3 = x4 = x5 = 0.0 and so EO is not really necessary and is used just to demonstrate the algorithm.
Evolutionary Optimization Parameters
In high-level pseudo-code, an EO algorithm works like this:
set up parameters
initialize a population of random solutions
loop until done
select two good parent solutions
use them to generate two child solutions
place children into population
immigrate a new solution into population
end loop
return best solution found
EO is a meta-heuristic, which means that it's really a set of guidelines that can be used to design a specific algorithm. There are many design choices you must make, such as how to select parent solutions, how to generate children solutions and how to replace old solutions with new solutions.
The demo program in Figure 1 begins by setting up nine parameters that are used by the EO algorithm. Compared to other optimization techniques, EO requires many free parameters (this is considered a weakness of EO).
The first parameter is the number of problem dimensions, or put another way, the number of x-values that must be found. For the demo problem this is 6 because the values for x0, x1, x2, x3, x4, and x5 must be found. When using EO for neural network training, the number of problem dimensions will be the number of network weights and bias values. In EO, a possible solution is represented by a virtual chromosome, which is realized as an array of type double. Each cell in the chromosome array is called a gene, so the problem dimension can also be referred to as the number of genes. There are many variations in genetic algorithm vocabulary. For example, the array that this article calls a chromosome is also called a genotype.
The second parameter used by EO is the population size, which is set to 50 in the demo. EO works with a collection of possible solutions rather than just a single solution. In general, the population size for an EO algorithm is often between 10 and 1,000.
The third and fourth EO parameters are minGene and maxGene, which are set to -10.0 and +10.0 respectively. These values define the range of possible initial values for each x-value (gene) in a solution (chromosome). When using EO to train a neural network, if the input data is normalized, then the vast majority of normalized values will be between -10 and +10, and therefore reasonable weights and bias values will also be between -10 and +10. If you use EO for some problem other than neural network training, you may have to change the values of minGene and maxGene.
The fifth EO parameter is the mutation rate, which is set to 0.20 in the demo. EO is an iterative process. In each iteration, each x-value in the chromosome array is mutated (changed) with probability equal to the mutation rate. EO is often very sensitive to parameter values, especially the mutation rate, and in general you must experiment with different values. That said, based on my experience, EO mutation rates between 0.10 and 0.50 typically work best. Note that mutation rate values for genetic algorithms that use a bit representation for solutions are typically much smaller than those used by EO algorithms that use real-valued solutions.
The sixth EO parameter is the mutation change factor, set to 0.01 in the demo. This value controls the magnitude of change in a gene/x-value if in fact the gene is mutated. Typically, values between 0.001 and 0.1 work well, but again, in many situations you must experiment a bit.
The seventh EO parameter is the selection pressure, often called tau in research literature, which is set to 0.40 in the demo. The selection pressure is used by the part of the algorithm that determines which pair of parent chromosomes will be selected to be used to generate new child solutions. You can think of selection pressure as loosely meaning the likelihood that the two best chromosomes will be selected. Typical effective values for tau range from 0.30 to 0.70.
The eighth and ninth EO parameters control how the EO main processing loop terminates. The max-generations parameter is hard limit on the maximum number of iterations of the main EO processing loop. In the demo max-generations is set to 5000 and was determined by some preliminary experimentation. The early-exit error, set to 0.000010 in the demo, establishes a short-circuit loop exit condition; if at any point in time the best solution found has an error less than the early-exit error, the processing loop breaks immediately.
Overall Demo Program Structure
To create the demo program I launched Visual Studio and created a C# console application named EvolutionaryOptimization. After the template code loaded into the editor, I deleted all references to .NET namespaces except for the one to the top-level System namespace. In the Solution Explorer window I renamed file Program.cs to EvolutionaryProgram.cs and VS automatically renamed class Program for me.
The overall program structure, with some minor edits to save space, is presented in Listing 1. The demo has most normal error-checking removed to keep the size of the code smaller and to keep the main ideas clear.
Listing 1: Demo Program Structure
using System;
namespace EvolutionaryOptimization
{
class EvolutionaryProgram
{
static Random rnd = new Random(0);
static void Main(string[] args)
{
Console.WriteLine("Begin Evolutionary Optimization demo");
Console.Write("Goal is to minimize f(x0,x1,x2,x3,x4,x5) = ");
Console.WriteLine("x0^2 + x1^2 + x2^2 + x3^2 + x4^2 + x5^2");
Console.Write("Known solution is 0.0 at ");
Console.WriteLine("x0 = x1 = x2 = x3 = x4 = x5 = 0.000000");
int dim = 6;
int popSize = 50;
double minX = -10.0;
double maxX = 10.0;
double mutateRate = 0.20;
double mutateChange = 0.01;
double tau = 0.40;
int maxGeneration = 5000;
double exitError = 0.00001;
Console.WriteLine("Setting problem dimension = " + dim);
// display values of other parameters
double[] bestSolution = Solve(dim, popSize, minX, maxX,
mutateRate, mutateChange, tau, maxGeneration, exitError);
Console.WriteLine("Best solution found:\n");
for (int i = 0; i < bestSolution.Length; ++i)
Console.Write(bestSolution[i] + " ");
double error = EvolutionaryProgram.Error(bestSolution);
Console.Write("(Absolute) error value at best solution = ");
Console.WriteLine(error.ToString("F6"));
Console.WriteLine("\nEnd Evolutionary Optimization demo\n");
Console.ReadLine();
}
static double[] Solve(int dim, int popSize, double minX,
double maxX, double mutateRate, double mutateChange,
double tau, int maxGeneration, double exitError) { . . }
private static Individual[] Select(int n,
Individual[] population, double tau) { . . }
private static Individual[] Reproduce(Individual parent1,
Individual parent2, double minGene, double maxGene,
double mutateRate, double mutateChange) { . . }
private static void Mutate(Individual child, double maxGene,
double mutateRate, double mutateChange) { . . }
private static void Place(Individual child1, Individual child2,
Individual[] population) { . . }
private static void Immigrate(Individual[] population,
int numGenes, double minGene, double maxGene,
double mutateRate, double mutateChange) { . . }
public static double Error(double[] x) { . . }
}
public class Individual : IComparable<Individual>
{
public double[] chromosome;
public double error;
private int numGenes;
private double minGene;
private double maxGene;
private double mutateRate;
private double mutateChange;
static Random rnd = new Random(0);
public Individual(int numGenes, double minGene,
double maxGene, double mutateRate, double mutateChange) { . . }
public int CompareTo(Individual other) { . . }
}
}
Most of the work is performed by method Solve. Method Solve calls helper methods Select (to pick two good parents), Reproduce (to generate two new child solutions), Place (to insert the children into the population) and Immigrate (to insert a new random solution into the population). Helper method Reproduce calls sub-helper method Mutate (to alter the new children slightly). Method Solve assumes the existence of a globally accessible class-scope Random object named rnd, an accessible Error function and an Individual class.
The Individual Class
Program-defined class Individual encapsulates a chromosome/solution. The class derives from IComparable so that Individual objects can be automatically sorted from best (smallest error) to worst (largest error). The Individual class definition is presented in Listing 2.
Listing 2: The Individual Class
public class Individual : IComparable<Individual>
{
public double[] chromosome; // a solution
public double error;
private int numGenes; // problem dimension
private double minGene;
private double maxGene;
private double mutateRate;
private double mutateChange;
static Random rnd = new Random(0);
public Individual(int numGenes, double minGene,
double maxGene, double mutateRate, double mutateChange)
{
this.numGenes = numGenes;
this.minGene = minGene;
this.maxGene = maxGene;
this.mutateRate = mutateRate;
this.mutateChange = mutateChange;
this.chromosome = new double[numGenes];
for (int i = 0; i < this.chromosome.Length; ++i)
this.chromosome[i] =
(maxGene - minGene) * rnd.NextDouble() + minGene;
this.error = EvolutionaryProgram.Error(this.chromosome);
}
public int CompareTo(Individual other)
{
if (this.error < other.error) return -1;
else if (this.error > other.error) return 1;
else return 0;
}
}
Array member chromosome represents a possible solution to the problem being investigated. Typically, standard genetic algorithms use a form of bit representation, while evolutionary algorithms use real values, but this vocabulary distinction is arbitrary. Member variable error holds the error associated with the object's chromosome/solution. This value is often named fitness but I prefer the name error in situations where the goal is to minimize some value such as neural network training error. For simplicity, members chromosome and error are declared with public scope but you may want to use private scope along with get and set properties.
The Individual class constructor generates a random solution, where each cell/gene of the chromosome array is between minGene and maxGene, using a class-scope Random object. Notice the constructor calls the globally accessible Error function to supply the value for the error member. An alternative, but in my opinion, messier approach, is to pass the error function to the constructor as a delegate.
The CompareTo method is coded so that when a Sort method is called on a collection of Individual objects, the objects will be sorted from smallest error (best) to largest error (worst).
The Error method is defined as:
public static double Error(double[] x)
{
double trueMin = 0.0;
double z = 0.0;
for (int i = 0; i < x.Length; ++i)
z += (x[i] * x[i]);
return Math.Abs(trueMin - z);
}
Here the absolute value of the difference between the true, known minimum value of the dummy function (0.0) and the computed value, z, is returned. Common alternatives are to return the squared difference between the true and computed values, or to return the square root of the squared difference. Notice all these approaches ensure that error is always a non-negative number.
The Solve Method
The Solve method is presented in Listing 3. The method begins by creating a population of random possible solutions. An alternative to consider is allowing the population size to vary over time, but this approach has not improved results for me. As each Individual object is created, its error is checked to see if it's the best error found so far. After population initialization, the main processing loop is prepared by setting up a loop counter gen (generation) and a Boolean done, which monitors early-exit error.
Listing 3: The Solve Method
static double[] Solve(int dim, int popSize, double minX,
double maxX, double mutateRate, double mutateChange,
double tau, int maxGeneration, double exitError)
{
Individual[] population = new Individual[popSize];
double[] bestSolution = new double[dim];
double bestError = double.MaxValue;
// population initialization
for (int i = 0; i < population.Length; ++i)
{
population[i] = new Individual(dim, minX, maxX,
mutateRate, mutateChange);
if (population[i].error < bestError)
{
bestError = population[i].error;
Array.Copy(population[i].chromosome, bestSolution, dim);
}
}
int gen = 0; bool done = false;
while (gen < maxGeneration && done == false)
{
if (gen % 200 == 0)
{
Console.WriteLine("\nGeneration = " + gen);
Console.WriteLine("Best error = " + bestError);
}
Individual[] parents = Select(2, population, tau);
Individual[] children = Reproduce(parents[0], parents[1],
minX, maxX, mutateRate, mutateChange);
Accept(children[0], children[1], population);
Immigrate(population, dim, minX, maxX, mutateRate,
mutateChange);
for (int i = popSize - 3; i < popSize; ++i)
{
if (population[i].error < bestError)
{
bestError = population[i].error;
population[i].chromosome.CopyTo(bestSolution, 0);
if (bestError < exitError)
{
done = true;
Console.WriteLine("Exit at generation " + gen);
}
}
}
++gen;
}
return bestSolution;
}
Inside the processing loop I print a progress message every 200 iterations. This is useful to monitor the the algorithm to make sure that the smallest error decreases over time and to verify that the algorithm is not oscillating. Method Select returns two good (but not necessarily the two best) solutions from the current population. Method Reproduce then uses the two good solutions to generate two child solutions. The idea is that by combining traits of good solutions, even better solutions are likely to be created. Method Place inserts the two new child solutions into the population, replacing the two worst solutions. Method Immigrate generates a new random solution and places it into the population.
At this point, three new solutions (the two children and the immigrant) have been placed into the population. These three solutions are checked to see if any of them have a new best solution, and if so, the early-exit error condition is checked to see if the processing loop should terminate before reaching maxGenerations iterations.
The Select Method
There are several techniques that can be used to select relatively good parent solutions from a population of solutions. Experience with genetic algorithms has shown that it's better to select two good, rather than the two best, solutions as parents because that approach generates more solution diversity and usually leads to better results. Method Select is presented in Listing 4.
Listing 4: The Select Method
private static Individual[] Select(int n, Individual[] population,
double tau)
{
int popSize = population.Length;
int[] indexes = new int[popSize];
for (int i = 0; i < indexes.Length; ++i)
indexes[i] = i;
for (int i = 0; i < indexes.Length; ++i)
{
int r = rnd.Next(i, indexes.Length);
int tmp = indexes[r];
indexes[r] = indexes[i];
indexes[i] = tmp;
}
int tournSize = (int)(tau * popSize);
if (tournSize < n) tournSize = n;
Individual[] candidates = new Individual[tournSize];
for (int i = 0; i < tournSize; ++i)
candidates[i] = population[indexes[i]];
Array.Sort(candidates);
Individual[] results = new Individual[n];
for (int i = 0; i < n; ++i)
results[i] = candidates[i];
return results;
}
Method Select begins by generating an array of indices, in order, that correspond to the indices of the population. Then the indices are shuffled into a random order using the Fisher-Yates algorithm. The shuffled indices are used to generate a collection of candidates. The candidates are sorted by error, and then the top n candidates are returned
This selection process is called tournament selection. The primary alternative is called roulette wheel selection. In tournament selection, a random percentage of the population is selected as candidates, and then the top two individuals from the candidates are returned. The percentage of the population is often called the Greek letter tau. Suppose tau is 0.40 and the population size is 50 as in the demo. This means 0.40 of the population, which is 20 individuals, will be initially selected as candidates. This 40 percent may or may not contain the two best individuals. Then the two best candidates are identified and returned. Larger values of tau increase the probability that the best individuals will be included in the candidate pool.
The Reproduce Method
The Reproduce method takes two parent solutions and uses them to create two child solutions. The code for method Reproduce is presented in Listing 5.
Listing 5: The Reproduce Method
private static Individual[] Reproduce(Individual parent1,
Individual parent2, double minGene, double maxGene,
double mutateRate, double mutateChange)
{
int numGenes = parent1.chromosome.Length;
int cross = rnd.Next(0, numGenes - 1);
Individual child1 = new Individual(numGenes, minGene, maxGene,
mutateRate, mutateChange);
Individual child2 = new Individual(numGenes, minGene, maxGene,
mutateRate, mutateChange);
for (int i = 0; i <= cross; ++i)
child1.chromosome[i] = parent1.chromosome[i];
for (int i = cross + 1; i < numGenes; ++i)
child2.chromosome[i] = parent1.chromosome[i];
for (int i = 0; i <= cross; ++i)
child2.chromosome[i] = parent2.chromosome[i];
for (int i = cross + 1; i < numGenes; ++i)
child1.chromosome[i] = parent2.chromosome[i];
Mutate(child1, maxGene, mutateRate, mutateChange);
Mutate(child2, maxGene, mutateRate, mutateChange);
child1.error = EvolutionaryProgram.Error(child1.chromosome);
child2.error = EvolutionaryProgram.Error(child2.chromosome);
Individual[] result = new Individual[2];
result[0] = child1;
result[1] = child2;
return result;
}
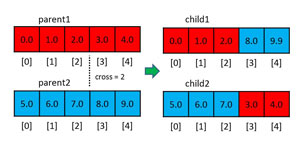
The reproduction process uses two techniques, crossover and mutation. Crossover is illustrated in Figure 2. The figure shows two parent chromosome arrays, each of which has five genes with dummy values. In crossover, a random crossover point is generated. In the figure, crossover is 2. The first child is a combination of the left half of the first parent and the right half of the second parent. The second child is a combination of the left half of the second parent and the right half of the first parent. One of several crossover alternatives is to use two or more crossover points.
 [Click on image for larger view.]
Figure 2. The Crossover Mechanism
[Click on image for larger view.]
Figure 2. The Crossover Mechanism
The Reproduce method implements crossover directly, but calls a helper method, Mutate, to perform mutation. Two minor alternative design choices that produce more symmetric code are to write a helper to perform crossover, or to implement mutation directly inside Reproduce.
The code for helper method Mutate is quite short:
private static void Mutate(Individual child, double maxGene,
double mutateRate, double mutateChange)
{
double hi = mutateChange * maxGene;
double lo = -hi;
for (int i = 0; i < child.chromosome.Length; ++i) {
if (rnd.NextDouble() < mutateRate) {
double delta = (hi - lo) * rnd.NextDouble() + lo;
child.chromosome[i] += delta;
}
}
}
The method walks through a chromosome. A random value is generated. If this value is less than the mutateRate, the current gene is mutated. Suppose that mutateChange = 0.01 and maxGene = 10.0 as in the demo. Their product is 0.01 * 10.0 = 0.10. Then a random delta between -0.10 and +0.10 is added to the current gene. So, larger values of mutateChange will generate larger changes when Mutate is called, which in turn will cause the EO algorithm to converge to a solution more quickly, at the expense of an increased risk of overshooting an optimal solution.
Notice that the mutation process does not constrain the new value of a gene. You may want to check to see if the new gene value is less than minGene or greater than maxGene, and if so, bring the new value back in range.
After two new child solutions have been created by method Reproduce, the children are inserted into the population by method Place:
private static void Place(Individual child1, Individual child2,
Individual[] population)
{
int popSize = population.Length;
Array.Sort(population);
population[popSize - 1] = child1;
population[popSize - 2] = child2;
return;
}
Method Place sorts the population which puts the two worst solutions at the end of the population array at indices [popSize-1] and [popSize-2]. These two worst solutions are replaced by the two new children. An important alternative is to probabilistically select two bad, but not necessarily the worst, solutions. You can use tournament selection to implement this alternative.
Immigration
The demo program uses a technique called immigration. Immigration is generally considered an option in genetic algorithms, but I have found immigration to be extremely useful in almost all situations where I use evolutionary optimization. The idea of immigration is to introduce new, random solutions into the population in order to prevent the population from stagnating at a non-optimal solution. The code for method Immigrate is:
private static void Immigrate(Individual[] population,
int numGenes, double minGene, double maxGene, double mutateRate,
double mutateChange)
{
Individual immigrant = new Individual(numGenes, minGene,
maxGene, mutateRate, mutateChange);
int popSize = population.Length;
population[popSize - 3] = immigrant;
}
A new, random Individual is generated. Because Immigrate is called immediately after method Place is called, and Place sorts the population, the population will still be sorted. Recall that Place inserts newly generated children at indices [popSize-1] and [popSize-2] so Immigrate places the immigrant solution at index [popSize-3]. An alternative is to place the immigrant at a random location in the population.
A Solid, But Slow, Solution
The code and explanation presented in this article should give you a solid foundation for understanding and experimenting with evolutionary optimization. In a future article I'll explain how evolutionary optimization can be used to train a neural network. Basically, a chromosome holds the neural network's weights and bias values, and the error term is the average of all errors between the network's computed outputs and the training data target outputs. There is no general consensus (that I'm aware of anyway) in the machine learning community about which of the three most common neural network training techniques -- back-propagation, particle swarm optimization and evolutionary optimization -- is best. Based on my experience evolutionary optimization often gives the best results, but is usually the slowest technique.