Neural Network Lab
Understanding Neural Network Batch Training: A Tutorial
There are two different techniques for training a neural network: batch and online. Understanding their similarities and differences is important in order to be able to create accurate prediction systems.
Training a neural network is the process of finding a set of weights and bias values so that computed outputs closely match the known outputs for a collection of training data items. Once a set of good weights and bias values have been found, the resulting neural network model can make predictions on new data with unknown output values.
There are two general approaches for neural network training, usually called "batch" and "online." The approaches are similar but can produce very different results. The general consensus among neural network researchers is that when using the back-propagation training algorithm, using the online approach is better than using the batch approach. In spite of the superiority of online training, it's important to understand how batch training works.
The best way to get a feel for where this article is headed is to take a look at the demo program in Figure 1. The demo program uses batch training in conjunction with the back-propagation training algorithm. The goal of the demo is to predict the species of an iris flower (setosa, versicolor or virginica) from petal length, petal width, sepal (a leaf-like structure) length and sepal width. After batch training on 120 items completed, the demo neural network gave a 96.67 percent accuracy (29 out of 30) on the test data.
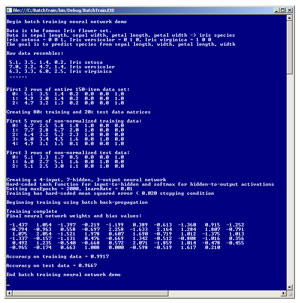 [Click on image for larger view.]
Figure 1. Batch Training in Action
[Click on image for larger view.]
Figure 1. Batch Training in Action
This article assumes you have a thorough grasp of neural network concepts and terminology, and at least intermediate-level programming skills. The demo is coded using C# but you should be able to refactor the code to other languages such as JavaScript or Visual Basic .NET without too much difficulty. Most normal error checking has been omitted from the demo to keep the size of the code small and the main ideas as clear as possible. The demo program is too large to present in its entirety in this article, but the complete program is available in the code download that accompanies this article.
Batch vs. Online Training
In the very early days of neural network, batch training was suspected by many researchers to be theoretically superior to online training. However, by the mid- to late-1990s, it became quite clear that when using the back-propagation algorithm, online training leads to a better neural network model in most situations.
In high-level pseudo-code the online training approach is:
loop maxEpochs times
for each training data item
compute weights and bias deltas for curr item
adjust weights and bias values using deltas
end for
end loop
In online training, weights and bias values are adjusted for every training item based on the difference between computed outputs and the training data target outputs. The batch approach is:
loop maxEpochs times
for each training item
compute weights and bias deltas for curr item
accumulate the deltas
end for
adjust weights and bias deltas using accumulated deltas
end loop
In batch training the adjustment delta values are accumulated over all training items, to give an aggregate set of deltas, and then the aggregated deltas are applied to each weight and bias.
Overall Program Structure
The overall structure of the demo program, with most WriteLine statements removed and a few minor edits, is presented in Listing 1. To create the demo, I launched Visual Studio and created a C# console application named BatchTrain. The demo has no significant .NET version dependencies. After the template code loaded, I removed all using statements except the one that references the top-level System namespace. In the Solution Explorer window, I renamed file Program.cs to the more descriptive NeuralBatchProgram.cs and Visual Studio renamed class Program for me.
Listing 1: Overall Program Structure
using System;
namespace BatchTrain
{
class NeuralBatchProgram
{
static void Main(string[] args)
{
Console.WriteLine("\nBegin batch training neural network demo");
double[][] allData = new double[150][];
allData[0] = new double[] { 5.1, 3.5, 1.4, 0.2, 0, 0, 1 };
. . .
allData[149] = new double[] { 5.9, 3.0, 5.1, 1.8, 1, 0, 0 };
double[][] trainData = null;
double[][] testData = null;
MakeTrainTest(allData, out trainData, out testData);
const int numInput = 4;
const int numHidden = 7;
const int numOutput = 3;
NeuralNetwork nn = new NeuralNetwork(numInput, numHidden, numOutput);
int maxEpochs = 2000;
double learnRate = 0.01;
nn.Train(trainData, maxEpochs, learnRate);
double[] weights = nn.GetWeights();
double trainAcc = nn.Accuracy(trainData);
double testAcc = nn.Accuracy(testData);
Console.WriteLine("\nAccuracy on test data = " + testAcc);
Console.WriteLine("\nEnd batch training neural network demo\n");
Console.ReadLine();
}
static void MakeTrainTest(double[][] allData, out double[][] trainData,
out double[][] testData) { . . }
static void ShowVector(double[] vector, int valsPerRow, int decimals,
bool newLine) { . . }
static void ShowMatrix(double[][] matrix, int numRows, int decimals,
bool newLine) { . . }
}
public class NeuralNetwork { . . }
}
The demo program hardcodes the 150-item Iris Data Set directly into an array-of-arrays-style matrix named allData. In most situations, your source data will be in a text file and you would write a helper method (named something like LoadData) to get the data into memory.
The demo program calls helper method MakeTrainTest to randomly split the 150-item data set into a 120-item training set and a 30-item test set. Then, the demo instantiates a 4-input, 7-hidden, 3-output fully connected, feed-forward neural network. Batch and online training can be used with any kind of training algorithm. Behind the scenes, the demo neural network uses back-propagation (by far the most common algorithm), which requires a maximum number of training iterations (2000 in this case) and a learning rate (set to 0.01).
After training completed, the demo computed the resulting model's accuracy on both the training data (99.17 percent, which is 129 correct species predictions out of 130 items) and the test data (99.67 percent, 29 out of 30 items). The test accuracy gives a rough approximation of how well the trained neural network would do with new data where the species isn't known.
The Neural Network Class
The definition of the batch training neural network begins:
public class NeuralNetwork
{
private static Random rnd;
private int numInput;
private int numHidden;
private int numOutput;
...
The Random object is used when initializing the weights and bias values. The definition continues:
private double[] inputs;
private double[][] ihWeights;
private double[] hBiases;
private double[] hOutputs;
private double[][] hoWeights;
private double[] oBiases;
private double[] outputs;
So far there's nothing to indicate this neural network will be using batch training. Matrix ihWeights holds the input-to-hidden weights. Array hBiases holds the hidden node bias values. Many neural network implementations code bias values as special weights with dummy 1.0 constant inputs, a design I consider somewhat artificial and error-prone. Array hOutputs holds the computed output values of the hidden nodes, and matrix hoWeights is for the hidden-to-output weights.
The definition continues:
private double[] oGrads;
private double[] hGrads;
private double[][] ihAccDeltas;
private double[] hBiasesAccDeltas;
private double[][] hoAccDeltas;
private double[] oBiasesAccDeltas;
Arrays oGrads and hGrads hold the output node gradients and hidden node gradients needed by the back-propagation algorithm. The next four fields are specific to batch training. Matrix ihAccDeltas holds the accumulated delta values (that is, small amounts that will be added) for the input-to-hidden weights. Similarly, fields hBiaseAccDeltas, hoAccDeltas, and oBiasesAccDeltas hold accumulated delta values for the hidden biases, the hidden-to-output weights, and the output biases.
The neural network exposes four public methods:
public NeuralNetwork(int numInput, int numHidden, int numOutput) { . . }
public double[] GetWeights() { . . }
public void Train(double[][] trainData, int maxEpochs, double learnRate) { . . }
public double Accuracy(double[][] testData) { . . }
The purpose of each of the public methods should be fairly clear to you if you examine the screenshot in Figure 1. The neural network contains nine private methods:
private static double[][] MakeMatrix(int rows, int cols) { . . }
private void SetWeights(double[] weights) { . . }
private void InitializeWeights() { . . }
private double[] ComputeOutputs(double[] xValues) { . . }
private static double HyperTanFunction(double x) { . . }
private static double[] Softmax(double[] oSums) { . . }
private void ComputeAndAccumulateDeltas(double[] tValues, double learnRate) { . . }
private double MeanSquaredError(double[][] trainData) { . . }
private static int MaxIndex(double[] vector) { . . }
Methods MakeMatrix, SetWeights and InitializeWeights are helpers that are used by the constructor. Methods HyperTanFunction and Softmax are the hardwired activation functions for the hidden and output layer nodes and are used by method ComputeOutputs. Method MeanSquaredError is called by public method Train in order to have an early (before maxEpochs) exit condition if training error drops below some low threshold value. Method MaxIndex is called by public method Accuracy to determine if the highest computed output probability matches the encoded output. Method ComputeAndAccumulateDeltas is a helper for public method Train.
The Train Method
The heart of batch training is in method Train, which is presented in Listing 2. Method Train follows the pseudo-code presented earlier. Inside the epoch-loop, the accumulation fields are zeroed-out at the start of each new pass through the training set. You might want to write a helper method named something like ZeroAccs to tidy up the 10 lines used in demo code.
Listing 2: Method Train
public void Train(double[][] trainData, int maxEpochs, double learnRate)
{
int epoch = 0;
double[] xValues = new double[numInput]; // Inputs
double[] tValues = new double[numOutput]; // Targets
while (epoch < maxEpochs)
{
double mse = MeanSquaredError(trainData);
if (mse < 0.020) break; // Consider parameterizing
// Zeroed-out accumulated weight deltas
for (int i = 0; i < numInput; ++i)
for (int j = 0; j < numHidden; ++j)
ihAccDeltas[i][j] = 0.0;
for (int i = 0; i < numHidden; ++i)
hBiasesAccDeltas[i] = 0.0;
for (int i = 0; i < numHidden; ++i)
for (int j = 0; j < numOutput; ++j)
hoAccDeltas[i][j] = 0.0;
for (int i = 0; i < numOutput; ++i)
oBiasesAccDeltas[i] = 0.0;
for (int i = 0; i < trainData.Length; ++i) // Each train item
{
Array.Copy(trainData[i], xValues, numInput); // Get curr x-values
Array.Copy(trainData[i], numInput, tValues, 0, numOutput); // Get curr t-values
ComputeOutputs(xValues); // Compute outputs (store them internally)
ComputeAndAccumulateDeltas(tValues, learnRate);
}
// Update all weights using the accumulated deltas
for (int i = 0; i < numInput; ++i)
for (int j = 0; j < numHidden; ++j)
ihWeights[i][j] += ihAccDeltas[i][j];
for (int i = 0; i < numHidden; ++i)
hBiases[i] += hBiasesAccDeltas[i];
for (int i = 0; i < numHidden; ++i)
for (int j = 0; j < numOutput; ++j)
hoWeights[i][j] += hoAccDeltas[i][j];
for (int i = 0; i < numOutput; ++i)
oBiases[i] += oBiasesAccDeltas[i];
++epoch;
}
}
The key to method Train is the call to helper ComputeAndAccumulateDeltas. After that call completes, the accumulated delta values (based on all training data) will be stored. Notice that because deltas are accumulated over all training items, the order in which training data is processed doesn't matter, as opposed to online training where it's critically important to visit items in a random order.
Accumulating Deltas
The definition of the accumulation routine begins by computing the output node gradients:
private void ComputeAndAccumulateDeltas(double[] tValues, double learnRate)
{
for (int i = 0; i < numOutput; ++i)
{
double derivative = (1 - outputs[i]) * outputs[i];
oGrads[i] = derivative * (tValues[i] - outputs[i]);
}
...
Recall that with back-propagation, gradients must be computed in the opposite direction of computing output values. This code makes the assumptions that softmax output activation is being used along with implicit mean squared error minimization. Next, the hidden node gradients are computed:
for (int i = 0; i < numHidden; ++i)
{
double derivative = (1 - hOutputs[i]) * (1 + hOutputs[i]);
double sum = 0.0;
for (int j = 0; j < numOutput; ++j)
{
double x = oGrads[j] * hoWeights[i][j];
sum += x;
}
hGrads[i] = derivative * sum;
}
Here, it's assumed that the hyperbolic tangent function is being used for hidden node activation. Next, input-to-hidden weight deltas are computed and accumulated:
for (int i = 0; i < numInput; ++i)
{
for (int j = 0; j < numHidden; ++j)
{
double delta = learnRate * hGrads[j] * inputs[i];
this.ihAccDeltas[i][j] += delta; // Accumulate
}
}
The demo program doesn't implement momentum. In general, based on my experience, when using normal online training, the use of momentum is beneficial, but when using batch training, momentum often leads to slower training.
Next, the hidden bias deltas are computed and accumulated:
for (int i = 0; i < numHidden; ++i)
{
double delta = learnRate * hGrads[i] * 1.0;
this.hBiasesAccDeltas[i] += delta;
}
Here, the dummy 1.0 term suggests that a bias can be considered a weight with a constant 1.0-value input. In a non-demo program you would want to remove the useless term. The method continues by computing and accumulating hidden-to-output weights:
for (int i = 0; i < numHidden; ++i)
{
for (int j = 0; j < numOutput; ++j)
{
double delta = learnRate * oGrads[j] * hOutputs[i];
this.hoAccDeltas[i][j] += delta;
}
}
Method ComputeAndAccumulateDeltas concludes by computing and accumulating the output node bias deltas:
...
for (int i = 0; i < numOutput; ++i)
{
double delta = learnRate * oGrads[i] * 1.0;
this.oBiasesAccDeltas[i] += delta;
}
}
Comparing Batch and Online Training
One of the reasons why it took researchers quite some time to determine that online training is preferable to batch training in most situations is that it's quite difficult to compare the two techniques. Take a look at the graph in Figure 2. The graph shows the mean squared error for two different neural networks during the first 100 epochs of training on the Iris Data Set.
 [Click on image for larger view.]
Figure 1. Batch vs. Online Error
[Click on image for larger view.]
Figure 1. Batch vs. Online Error
From the graph, it's clear that, for this example at least, traditional online training is both faster and less volatile than batch training. That said, however, the training parameters for the two neural networks were different, and it's possible to construct an example where batch training appears better than online training.
So, when should you ever consider using batch training? There's no good answer to this question. Training a neural network requires quite a bit of trial and error. I generally try online training first, and then, if I'm unable to get good results, I'll give batch training a try. Every now and then, for me at least, batch training works better than online training.
If you want more information on this topic, I recommend the 2003 research paper I used as the basis for this article: "The General Inefficiency of Bach Training for Gradient Descent Learning" by D. Wilson and T. Martinez (PDF).
Want more? Read the rest of James McCaffrey's Neural Network Lab columns.