Neural Network Lab
Customize Neural Networks with Alternative Activation Functions
Here's how to use non-standard activation functions to customize your neural network system.
Understanding how to use non-standard activation functions allows you to customize a neural network system. A neural network loosely models biological synapses and neurons. Neural network (NN) classifiers have two activation functions. One activation function is used when computing the values of nodes in the middle, hidden layer, and one function is used when computing the value of the nodes final, output layer.
Computing the values of an NN classifier's output nodes always uses the softmax activation function because the sum of the output values is 1.0 and so the values can be interpreted as probabilities for each class. For example, if your goal is to predict the political leaning (conservative, moderate, liberal) of a person based on predictor features such as age, annual income, state of residence and so on, then the NN classifier will have three output nodes. A set of output values might be something like (0.20, 0.70, 0.10), which would indicate the predicted political leaning is moderate.
There are two common activation functions used for NN hidden layer nodes, the logistic sigmoid function (often shortened to log-sigmoid or just sigmoid if the meaning is clear from context) and the hyperbolic tangent function (usually shortened to tanh). But using other hidden layer activation functions is possible.
The best way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. The demo program begins by creating 1,000 lines of synthetic data. Each data item corresponds to a problem where there are five numeric input values and the class to predict has three possible values. After the 1,000 data items were generated, the demo program randomly split the data into an 800-item set for training the NN and a 200-item set to be used to estimate the overall predictive accuracy of the final model.
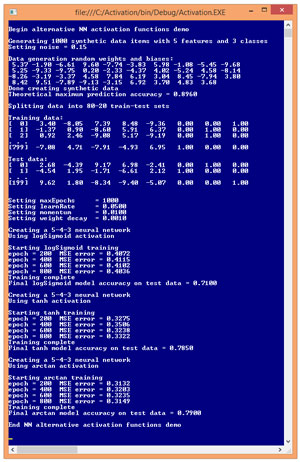Figure 1. Alternative Activation Functions Demo
The demo program creates and trains three neural networks, each with a different hidden layer activation function. The first NN uses the common log-sigmoid function and has a model accuracy of 71.00 percent (142 out of 200 correct). The second NN uses the common tanh function and has a model accuracy of 78.50 percent (157 out of 200 correct). The third NN uses an uncommon alternative activation function named arctangent (usually shortened to arctan) and has a model accuracy of 79.00 percent (158 out of 200 correct).
This article assumes you have a basic familiarity with neural networks but doesn't assume you know anything about alternative activation functions. The demo program is too long to present in its entirety but the complete program is available in the code download that accompanies this article.
Understanding Activation Functions
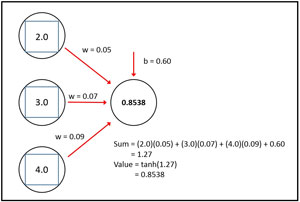
Figure 2 illustrates how NN hidden node activation works. The diagram represents three input nodes and just one hidden node to keep the main ideas clear. The three input nodes have values 2.0, 3.0 and 4.0. The three associated input-to-hidden weight values are 0.05, 0.07 and 0.09. The hidden node has a bias value of 0.60. Many references treat a bias value as an additional weight that has a dummy input value of 1.
[Click on image for larger view.]
Figure 2. Activation Function Example
To compute the value of the hidden node, first the sum of the inputs times their weights, plus the bias value, is calculated: (2.0)(0.05) + (3.0)(0.07) + (4.0)(0.09) + 0.60 = 1.27. The value of the hidden node is determined by feeding the sum to the activation function. In the case of the tanh function, tanh(1.27) = 0.8538. This value would be used later when computing the value of the output nodes.
As it turns out, the preliminary, pre-activation sum (1.27 in the example) isn't important when using the common log-sigmoid or tanh activation functions, but the sum is needed during training when using an alternative activation function such as arctan.
The graph in Figure 3 shows the log-sigmoid, tanh and arctan functions. All three functions have a flattened S shape. The common log-sigmoid function accepts any value and returns a result between 0 and 1. The common tanh function accepts any value and returns a result between -1 and +1. The uncommon arctan function accepts any value and returns a result between -Pi / 2 and +Pi / 2, or roughly between -1.6 and +1.6. In theory, because the arctan function is slightly flatter than the log-sigmoid and tanh functions, arctan may have a slightly better ability to discriminate between similar input values.
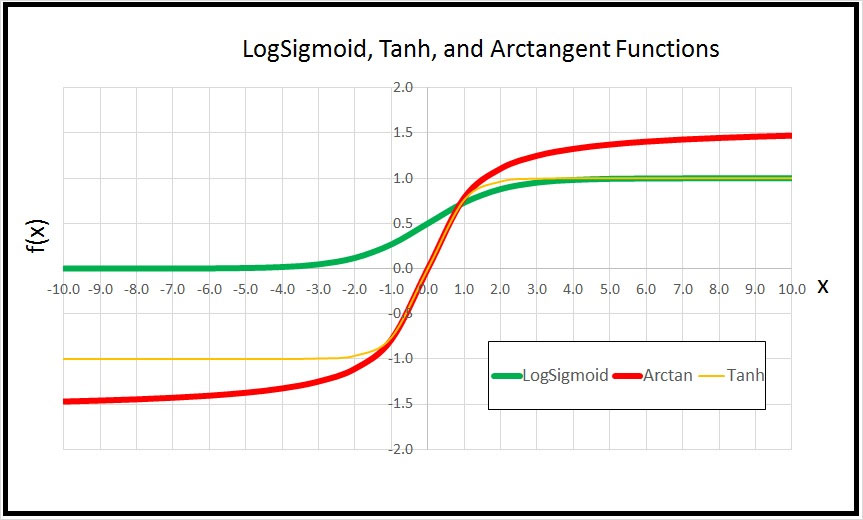Figure 3. Activation Functions Comparison
The Effect of the Activation Function on Training
Training an NN is the process of finding values for the weights and biases. This is done by examining different weight and bias values to find the values where the difference between computed output values (using training data input values) and the known target output values in the training data is minimized.
There are several different NN training algorithms, but by far the most common technique is called back-propagation. Back-propagation uses the calculus derivative of the hidden layer activation function. Your college calculus is likely to be a bit rusty. At best. Suppose a math function is y = 4x^3 (where the ^ character means exponentiation). The derivative of the function is y' = 12x^2. The point is that the derivative of a function almost always depends on x, the input value.
The log-sigmoid function is y = 1 / (1 + e^-x) where e is the special math constant 2.71828. So you'd expect the derivative to have the term x in it. However, due to some algebra coincidences, the derivative of log-sigmoid is (y)(1 - y). In other words, the derivative of log-sigmoid can be expressed in terms of the output value y. As you'll see shortly, this is very convenient when coding.
Similarly, the tanh function is y = (e^x - e^-x) / (e^x + e^-x). It's derivative is (1 - y)(1 + y). Again, by an algebra coincidence, the derivative of the tanh function can be expressed in terms of the output value y.
All reasonable alternative NN activation functions have derivatives that contain x. For example, the arctan function is y = 1/2 * log((1 + x) / (1 - x)). Its derivative is 1 / (1 + x^2).
The so-called stochastic version of the back-propagation algorithm, expressed in high-level pseudo-code with a few important details omitted, is:
loop until satisfied
for-each training item
peel off training input values and target output values
compute NN output values using current weights
compute derivative of output layer activation function
compute derivative of hidden layer activation function
use derivatives to update weights and biases
end-for
end-loop
return final weight and bias values
If you examine the pseudo-code you'll notice the derivative of the hidden layer activation function is needed. But just before the derivative is needed, the hidden node values are calculated as part of the process that computes the values of the output nodes. These hidden node values are exactly what are needed to compute the derivative of the log-sigmoid function or the tanh function. This makes coding relatively easy.
For alternative activation functions such as arctan, you need to save the input values. If you refer back to the diagram in Figure 2, you need to save the preliminary, pre-activation sum (1.27 in the diagram) in order to calculate the derivative. But if you use standard log-sigmoid or tanh activation, you only need the output value (0.8538), which is already saved as the value of the hidden node. For example, for the hidden node in Figure 2, if you're using the common tanh function, the derivative term is (y)(1 - y) = (0.8538)(1 - 0.8538). But if you're using the arctan function, the derivative term is 1 / (1 + x^2) = 1 / (1 - (1.27)^2).
To summarize, when using the common log-sigmoid or tanh functions for hidden node activation, if you use back-propagation training, calculating the derivative of the hidden layer function is easy because the value needed has already been calculated and saved. But if you use an alternative activation function such as arctan, you must save the pre-activation sum when computing the hidden node values.
Implementing an NN with an Alternative Activation Function
To create the demo, I launched Visual Studio and created a new C# console application named Activation. After the template code loaded, in the Solution Explorer window, I renamed file Program.cs to ActivationProgram.cs and allowed Visual Studio to automatically rename class Program for me.
The demo program has no significant .NET dependencies so any version of Visual Studio should work. In the editor window, at the top of the template-generated code, I deleted all unnecessary using statements, leaving just the reference to the top-level System namespace. The program structure, with a few minor edits to save space, is presented in Listing 1.
Listing 1: Program Structure
using System;
namespace Activation
{
class ActivationProgram
{
static void Main(string[] args)
{
Console.WriteLine("Begin activation demo");
// Generate data, split into training and test sets
int maxEpochs = 1000;
double learnRate = 0.05;
double momentum = 0.01;
double decay = 0.001;
// Display training parameters
string activation = "logSigmoid";
Console.WriteLine("Using " + activation +
" activation");
NeuralNetwork nn = new NeuralNetwork(numInput,
numHidden, numOutput, activation);
double[] weights = nn.Train(trainData, maxEpochs,
learnRate, momentum, decay);
double testAcc = nn.Accuracy(testData);
Console.WriteLine("Final " + activation +
" model accuracy on test data = " +
testAcc.ToString("F4"));
// Create, train, evaluate a tanh NN
// Create, train evaluate an arctan NN
Console.WriteLine("End demo");
Console.ReadLine();
} // Main
// Helper methods to create and display data go here
}
public class NeuralNetwork
{
private int numInput;
private int numHidden;
private int numOutput;
private double[] inputs;
private double[][] ihWeights;
private double[] hBiases;
private double[] hOutputs;
private double[][] hoWeights;
private double[] oBiases;
private double[] outputs;
private string activation;
private double[] hSums;
private Random rnd;
public NeuralNetwork(int numInput, int numHidden,
int numOutput, string activation)
{
this.numInput = numInput;
this.numHidden = numHidden;
this.numOutput = numOutput;
this.inputs = new double[numInput];
this.ihWeights = MakeMatrix(numInput, numHidden);
this.hBiases = new double[numHidden];
this.hOutputs = new double[numHidden];
this.hoWeights = MakeMatrix(numHidden, numOutput);
this.oBiases = new double[numOutput];
this.outputs = new double[numOutput];
this.activation = activation;
this.hSums = new double[numHidden];
this.rnd = new Random(0);
this.InitializeWeights();
} // ctor
// Methods and helpers to train and evaluate NN here
} // NeuralNetwork class
} // ns
All neural network functionality is contained in a program-defined NeuralNetwork class. The key difference between the demo NN definition and a more common definition is the inclusion of a class string member named activation. A string value of "logSigmoid," "tanh", or "arctan" is passed to the constructor and this value determines which hidden layer activation function will be used, which in turn determines how the derivative term will be calculated in the Train method.
Using magic strings like "logSigmoid" is a weak design choice in most situations. A more robust approach would be to use an Enumeration type. I used the string approach for simplicity and clarity.
Notice that the NeuralNetwork class definition has a member named hSums (hidden node sums), which is an array with length equal to the number of hidden nodes. The hSums array stores the hidden node pre-activation sums, which are computed by class method ComputeOutputs. The values in hSums are used by class method Train when computing the derivative if the arctan activation function has been specified.
A Few Comments
The use of alternative activation functions was studied by researchers in the 1990s. Although there weren't many studies done, the consensus conclusion was that using an alternative activation function sometimes improved NN model accuracy and sometimes did not. By the late 1990s, the use of the log-sigmoid and tanh functions for hidden node activation had become the norm.
So, the question is, should you ever use an alternative activation function? In my opinion, for day-to-day usage (if there even is such a concept for neural networks), the tanh function for hidden node activation is fine. But I'm not entirely convinced that tanh and log-sigmoid are always the best choices. I suspect it's entirely possible that for some classification problems an alternative activation function might produce a significantly better NN model.
If you're interested in exploring alternative activation functions, I recommend that you try and track down a relatively obscure 1991 research paper titled, "Efficient Activation Functions for the Back-Propagation Neural Network," by S. K. Kenue (you can check out the text at the IEEE Society library). The author presents six alternative activation functions. I experimented with the proposed alternatives using the demo program presented in this article as a framework, but did not get consistent results.
About the Author
Dr. James McCaffrey works for Microsoft Research in Redmond, Wash. He has worked on several Microsoft products including Azure and Bing. James can be reached at [email protected].