In-Depth
A More Efficient Text Pattern Search Using a Trie Class in .NET
The trie data structure is one alternative method for searching text that can be more efficient than traditional search approaches. Here's a trie class you can create in C#.
- By Arnaldo Pérez Castaño
- 10/20/2015
The proliferation of digital texts and textual databases during the second half of the last century produced the need for efficient search methods and efficient data structures. These data structures were necessary in order to support the storage of textual data in a manner in which a preprocessing stage would present the possibility of having subsequent search, insertion and deletion operations. Data structures offered a step up on efficiency, guaranteeing an enhancement compared to what some of the classical data structures of the moment were providing in terms of computational space and time consumption.
The trie -- which owes its name to information retrieval (probably its main field of application) and was originally described by https://en.wikipedia.org/wiki/Trie E. Fredkin in the 60s -- is one of these data structures. A trie presents itself as an alternative to the classical list and other data structures that we usually use for storing text. Its main goal is to provide an efficient way (in terms of space and time) for searching, inserting and deleting text.
In this article, I'll describe a Trie class created in C# and make some comparisons with different data structures provided by the .NET framework. I'll also demonstrate why this data structure can prove to be a necessary and positive alternative when efficiency is required.
How a Trie Works
The tree satisfying all of the following points is what we usually consider as a trie:
- Its main goal is to provide an efficient manner to search, insert and delete a string (textual representation as we know it in C#).
- Each node can have up to n children, being n the number of characters in the alphabet to which all strings (texts) belong. In the ordinary case the alphabet would be the same we have always known (a, b, c, d, ... z).
- Each node contains a value represented as a type char.
The root node always has the special char value '^'.
- Each string inserted in the Trie and all of its prefixes can be found by following a path from the root node to some other node.
- The end of a string is marked by the presence of some child node with value '$'. The character '$' is assumed to not be part of the alphabet.
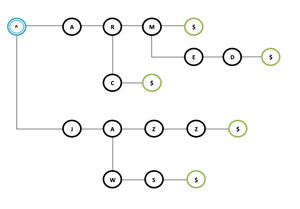
Figure 1 shows an example trie, depicting this data structure after having inserted the set S = {"arm", "armed", "arc", "jazz", "jaws"}.
 [Click on image for larger view.]
Figure 1: An Example Trie with Set S Inserted
[Click on image for larger view.]
Figure 1: An Example Trie with Set S Inserted
This representation has a number benefits:
-
For two given strings x, y the common prefix of x and y is stored only once, therefore it reduces the spatial cost of the Trie.
- The operations of search, insertion and deletion for a given string s can be made in O(m) where m is the length of s.
- Even though the preprocessing stage (insertion) could not be as efficient as it is in other data structures, it pays off in situations where you frequently need to search text patterns and the insertion/deletion operations are not frequent.
- It's easy to implement and understand.
How would a classical data structure, like the list, store the previous set? Figure 2 shows a list, which stores every element in a separate slot without relating in any way the elements contained in separate slots thus a common prefix for several strings is stored for each of these strings which implies a higher spatial cost compared to the trie.
 [Click on image for larger view.]
Figure 2: A List Stores Every Element in a Separate Slot
[Click on image for larger view.]
Figure 2: A List Stores Every Element in a Separate Slot
All the operations in the trie depend upon a method or subroutine, known as Prefix, in charge of finding the prefix from the string that is already present in the structure. The implementation of Prefix is very simple: Only a match of each character of the string with values of the Nodes along a path (started from the root) that ends when there is no longer a match, returns the last node that matched. In the previous trie a call to Prefix("JA") will return the node with value "A" and children nodes with values "Z" and "W".
Considering the Prefix method, a search operation would call to the Prefix method, checking the string was completely matched and the resulting node from the Prefix method has a child node with value "$".
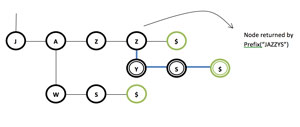
The insertion operation also relies on the Prefix method, in this case to discover the node in which the insertion of new nodes should begin. If we insert the string "JAZZY" in the previous trie (see Figure 3), then a call to Prefix("JAZZYS") will return the node corresponding to the second Z; starting in this node the suffix of the string not matched ("YS") will be inserted as new nodes in the tree.
 [Click on image for larger view.]
Figure 3: Inserting the JAZZY String
[Click on image for larger view.]
Figure 3: Inserting the JAZZY String
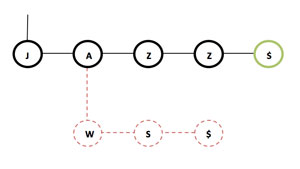
The deletion operation is similar to the insertion; in this case we find the complete path that represents the string (if any) and then go backwards, deleting leaf nodes (nodes with no child). To delete "JAWS" from the trie (see Figure 4), we just delete the nodes with values: $, S, W. The node with value "A" is not deleted as it is linked to the "JAZZ" string and is not a leaf.
 [Click on image for larger view.]
Figure 4: Deleting JAWS
[Click on image for larger view.]
Figure 4: Deleting JAWS
To implement a trie we'll need to develop a Node class, shown in Listing 1.
Listing 1: Node Class
public class Node
{
public char Value { get; set; }
public List<Node> Children { get; set; }
public Node Parent { get; set; }
public int Depth { get; set; }
public Node(char value, int depth, Node parent)
{
Value = value;
Children = new List<Node>();
Depth = depth;
Parent = parent;
}
public bool IsLeaf()
{
return Children.Count == 0;
}
public Node FindChildNode(char c)
{
foreach (var child in Children)
if (child.Value == c)
return child;
return null;
}
public void DeleteChildNode(char c)
{
for (var i = 0; i < Children.Count; i++)
if (Children[i].Value == c)
Children.RemoveAt(i);
}
}
Notice the Node class includes a Parent field. This field is useful when implementing the delete operation, as we'll need to go backwards from child node to parent node. The Depth field is useful for knowing how long a given prefix is and the FindChildrenValue method finds and returns the child node whose value equals c. The DeleteChildNode method is useful in the deletion operation. The final implementation of the trie class is shown in Listing 2.
Listing 2: Complete Trie Class
public class Trie
{
private readonly Node _root;
public Trie()
{
_root = new Node('^', 0, null);
}
public Node Prefix(string s)
{
var currentNode = _root;
var result = currentNode;
foreach (var c in s)
{
currentNode = currentNode.FindChildNode(c);
if (currentNode == null)
break;
result = currentNode;
}
return result;
}
public bool Search(string s)
{
var prefix = Prefix(s);
return prefix.Depth == s.Length && prefix.FindChildNode('$') != null;
}
public void InsertRange(List<string> items)
{
for (int i = 0; i < items.Count; i++)
Insert(items[i]);
}
public void Insert(string s)
{
var commonPrefix = Prefix(s);
var current = commonPrefix;
for (var i = current.Depth; i < s.Length; i++)
{
var newNode = new Node(s[i], current.Depth + 1, current);
current.Children.Add(newNode);
current = newNode;
}
current.Children.Add(new Node('$', current.Depth + 1, current));
}
public void Delete(string s)
{
if (Search(s))
{
var node = Prefix(s).FindChildNode('$');
while (node.IsLeaf())
{
var parent = node.Parent;
parent.DeleteChildNode(node.Value);
node = parent;
}
}
}
}
Trie vs. .NET Collections
So, why would you want to develop a trie in .NET with all the optimized data structures available in the platform?
The main difference between a trie and .NET collections resides in the fact that the first allows you to search an entire string, a prefix and even a pattern efficiently. To search a pattern like "aa*bb" indicating the set of elements (strings) starting with "aa" and ending in "bb" the .NET collections must rely on LINQ extension methods, which are always costly.
To go deeper into answering the question, let's compare search efficiencies between the trie implemented above and some data structures available in the .NET platform:
- List<T>
- SortedList
- HashSet<T>
To make the comparison reliable, we'll use a StopWatch to measure the time in ticks (1 tick = 100 nanoseconds) taken by each data structure to find some text pattern. We'll also use a 58,604-word dataset to insert and later search patterns.
We set up our experiment in a console application. To avoid unnecessary calls to instance methods, we omit calling the Search method and instead just ask the two questions (length of path == length string && last node in the path contains a child node with value '$') directly after having executed the Prefix algorithm, which basically give us all the information we need to decide whether a pattern belongs to the trie. The body of this experiment is in Listing 3.
Listing 3: List<T> Experiment with StopWatch
static void Main()
{
var items = new List<string> { "armed" , "armed", "jazz", "jaws" };
var stream = new StreamReader(@"C:/word2.txt");
while (!stream.EndOfStream)
items.Add(stream.ReadLine());
var stopwatch = new Stopwatch();
var trie = new Trie();
var hashset = new HashSet<string>();
const string s = "gau";
stopwatch.Start();
trie.InsertRange(items);
stopwatch.Stop();
Console.WriteLine("Trie insertion in {0} ticks", stopwatch.ElapsedTicks);
stopwatch.Reset();
stopwatch.Start();
for (int i = 0; i < items.Count; i++)
hashset.Add(items[i]);
stopwatch.Stop();
Console.WriteLine("HashSet in {0} ticks", stopwatch.ElapsedTicks);
stopwatch.Reset();
Console.WriteLine("-------------------------------");
stopwatch.Start();
var prefix = trie.Prefix(s);
var foundT = prefix.Depth == s.Length && prefix.FindChildNode('$') != null;
stopwatch.Stop();
Console.WriteLine("Trie search in {0} ticks found:{1}", stopwatch.ElapsedTicks, foundT);
stopwatch.Reset();
stopwatch.Start();
var foundL = hashset.FirstOrDefault(str => str.StartsWith(s));
stopwatch.Stop();
Console.WriteLine("HashSet search in {0} ticks found:{1}", stopwatch.ElapsedTicks, foundL);
trie.Delete("jazz");
Console.Read();
}
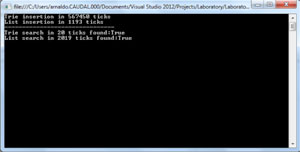
The results of the first comparison (List vs. Trie) is shown in Figure 5.
 [Click on image for larger view.]
Figure 5: Results of List vs. Trie
[Click on image for larger view.]
Figure 5: Results of List vs. Trie
The trie clearly searches more efficiently but loses the battle in the Insertion operation. But as I noted earlier, if you know you'll get frequent search operations instead of frequent insertion/deletion operations, it definitely pays off to implement the trie.
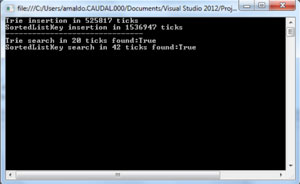
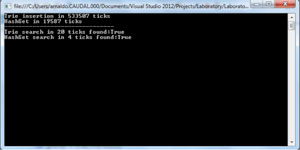
Now let's compare SortedList (see Figure 6) and the HashSet<T> (see Figure 7) In the first case, we present results when the set S was added as keys of the collection, which represents the most efficient alternative.
 [Click on image for larger view.]
Figure 6: Results of SortedList
[Click on image for larger view.]
Figure 6: Results of SortedList
As you can see, SortedList executes a fast search. The only problem with this approach (adding texts as keys) is that you cannot have duplicated texts in the database.
 [Click on image for larger view.]
Figure 7: HashSet<T> Results
[Click on image for larger view.]
Figure 7: HashSet<T> Results
The HashSet<T> beats the trie when it comes down to searching an entire string. What about searching a pattern? To search a pattern in a HashSet you'll need to use a LINQ extension method (the same goes for other .NET collections) which will considerably increase the temporal complexity of the search pattern operation:
var foundl =HashSet.FirstOrDefault(str => str.StartWith(s)0;
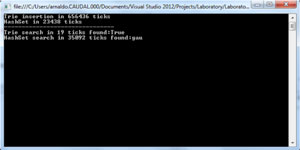
Figure 8 shows the results after having executed the LINQ query.
 [Click on image for larger view.]
Figure 8: HashSet<T> Results Improved with LINQ Query
[Click on image for larger view.]
Figure 8: HashSet<T> Results Improved with LINQ Query
Hopefully, after having made all the prior comparisons many of the readers will have cleared any doubts regarding the trie and will consider adding it to their arsenal of Collections. The .NET platform doesn't include a similar data structure but you can easily include it by reviewing the trie Class code illustrated in this article.