The Data Science Lab

How to Do Neural Binary Classification Using Keras

• By James McCaffrey
• 08/30/2018

The goal of a binary classification problem is to make a prediction that can be one of just two possible values. For example, you might want to predict the sex (male or female) of a person based on their age, annual income and so on. Somewhat surprisingly, binary classification problems require a different set of techniques than classification problems where the value to predict can be one of three or more possible values.

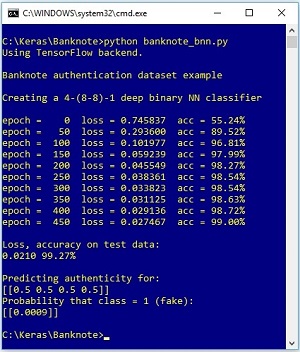
There are many different binary classification algorithms. In this article I'll demonstrate how to perform binary classification using a deep neural network with the Keras code library. The best way to understand where this article is headed is to take a look at the screenshot of a demo program in Figure 1.

The demo program creates a prediction model on the Banknote Authentication dataset where the problem is to predict whether a banknote (think dollar bill or euro) is authentic or a forgery, based on four predictor variables. The demo loads a training subset into memory then creates a 4-(8-8)-1 deep neural network.

After training for 500 iterations, the resulting model scores 99.27 percent accuracy on a held-out test dataset. The demo concludes by making a prediction for a hypothetical banknote that has average input values. The probability that the unknown item is a forgery is only 0.0009, therefore the conclusion is that the banknote is authentic.

This article assumes you have intermediate or better programming skill with a C-family language and a basic familiarity with machine learning. All of the demo code is presented in this article. The source code and the data file used by the demo are also available in the download that accompanies this article. All normal error checking has been removed to keep the main ideas as clear as possible.

Installing Keras
Keras is a code library that provides a relatively easy-to-use Python language interface to the relatively difficult-to-use TensorFlow library. Installing Keras involves three main steps. First you install Python and several required auxiliary packages such as NumPy and SciPy, then you install TensorFlow, then you install Keras.

Although it's possible to install Python and the packages required to run Keras separately, it's much better to install a Python distribution, which is a collection containing the base Python interpreter and additional packages that are compatible with each other. For my demo, I installed the Anaconda3 4.1.1 distribution (which contains Python 3.5.2), TensorFlow 1.7.0 and Keras 2.1.5.

Understanding the Data
The Banknote Authentication dataset has 1,372 items. The raw data looks like:

3.6216, 8.6661, -2.8073, -0.44699, 0
4.5459, 8.1674, -2.4586, -1.4621, 0
. . . 
-2.5419, -0.65804, 2.6842, 1.1952, 1

The first four values on each line are the predictor values. The last value on each line is either 0 (authentic) or 1 (forgery). The predictor values are from a digital image of each banknote and are variance, skewness, kurtosis and entropy.

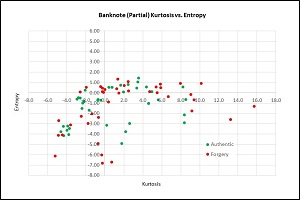
Because there are four independent variables, it's not possible to easily visualize the dataset but you can get a rough idea of the data from the graph in Figure 2. The graph shows the kurtosis and entropy values for 80 of the 1,372 data items. The point here is that simple linear prediction algorithms, such as logistic regression, would perform very poorly on this data.

In most scenarios, it's advisable to normalize your data so that values with large magnitudes don't overwhelm small values. I used min-max normalization on the four predictor variables. For each variable, I computed the min value and the max value, and then for every value x, normalized as (x - min) / (max - min). After min-max normalization, all values will be between 0.0 and 1.0 where 0.0 maps to the smallest value, 1.0 maps to the largest value, and 0.5 maps to a middle value.

After normalizing, I split the 1,372-item normalized dataset into a training set (80 percent = 1,097 items) and test set (20 percent = 275 items). Data preprocessing isn't conceptually difficult, but it's almost always quite time-consuming and annoying. Many of my colleagues like to use the pandas (originally "panel data," now "Python data analysis library") package to manipulate data, but pandas has a hard learning curve so I prefer to use raw Python.

The Demo Program
The structure of demo program, with a few minor edits to save space, is presented in Listing 1. I indent with two spaces rather than the usual four spaces to save space. And note that Python uses the "\" character for line continuation. I used Notepad to edit my program. Yes, Notepad. Many of my colleagues prefer Visual Studio or VS Code, both of which have excellent support for Python.

Listing 1: The Boston Housing Demo Program Structure

# banknote_bnn.py
import numpy as np
import keras as K
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'  # suppress CPU msg

class MyLogger(K.callbacks.Callback):
  def __init__(self, n):
    self.n = n   # print loss & acc every n epochs

  def on_epoch_end(self, epoch, logs={}):
    if epoch % self.n == 0:
      curr_loss =logs.get('loss')
      curr_acc = logs.get('acc') * 100
      print("epoch = %4d loss = %0.6f acc = %0.2f%%" % \
        (epoch, curr_loss, curr_acc))

def main():
  print("Banknote authentication example ")
  np.random.seed(1)

  # 1. load data into memory
  # 2. define 4-(x-x)-1 deep NN model
  # 3. compile model
  # 4. train model
  # 5. evaluate model
  # 6. make a prediction

if __name__=="__main__":
  main()

The file is named banknote_bnn.py where the "bnn" stands for binary neural network classifier. For simplicity, the demo imports the entire Keras library. An alternative is to import just the modules or functions needed. The os package is used just to suppress an annoying startup message.

The demo defines a helper class MyLogger. This is used to display custom progress information during training every n iterations where n is set to 50 in the demo. A custom logger is optional because Keras can be configured to display a built-in set of information during training. All the control logic for the demo program is contained in a single main() function. Program execution begins by setting the global numpy random seed so results will be reproducible.

Loading Data into Memory
The demo loads the training data in memory using the NumPy loadtxt() function:

train_file = ".\\Data\\banknote_train_mm_tab.txt"
test_file = ".\\Data\\banknote_test_mm_tab.txt"

train_x = np.loadtxt(train_file, delimiter='\t',
  usecols=[0,1,2,3], dtype=np.float32)
train_y = np.loadtxt(train_file, delimiter='\t',
  usecols=[4], dtype=np.float32) 

The code assumes that the data is located in a subdirectory named Data. The loadtxt() function has a lot of optional parameters. In this case, the function call specifies that the data is tab-delimited and that there isn't a header row to skip. The float32 datatype is the default for Keras so I could have omitted specifying it explicitly. After loading the training dataset into memory, the test dataset is loaded in the same way:

test_x = np.loadtxt(test_file, delimiter='\t', 
  usecols=[0,1,2,3], dtype=np.float32)
test_y =np.loadtxt(test_file, delimiter='\t',
  usecols=[4], dtype=np.float32)

An alternative design approach to the one used in the demo is to load the entire source dataset into a matrix in memory, and then split the matrix into training and test matrices.

Creating the Neural Network
The demo creates the 4-(8-8)-1 neural network model with these statements:

my_init = K.initializers.glorot_uniform(seed=1)
model = K.models.Sequential()
model.add(K.layers.Dense(units=8, input_dim=4,
  activation='tanh', kernel_initializer=my_init)) 
model.add(K.layers.Dense(units=8, activation='tanh',
  kernel_initializer=my_init)) 
model.add(K.layers.Dense(units=1, activation='sigmoid',
  kernel_initializer=my_init))

An initializer object is generated, using a seed value of 1 so that the neural network model will be reproducible. The Glorot initialization algorithm is a relatively advanced technique that often works better than a random uniform algorithm. Neural networks are often highly sensitive to initializations so when things go wrong, this is one of the first areas to investigate.

The number of input nodes, four in this case, is determined by the structure of the problem data. The number of hidden layers (two) and the number of nodes in each hidden layer (eight) are free parameters (often called hyperparameters), that must be determined by trial and error. The number of output nodes, one, and the output activation function, sigmoid, are always used for binary regression problems.

The neural network model is compiled like so:

simple_sgd = K.optimizers.SGD(lr=0.01)  
model.compile(loss='binary_crossentropy',
  optimizer=simple_sgd, metrics=['accuracy'])  

The model is configured with the stochastic gradient descent with a learning rate of 0.01. Stochastic gradient descent is the most basic form of optimization algorithm. The Adam (adaptive moment estimation) algorithm often gives better results. The optimization algorithm, and its parameters, are hyperparameters. The loss function, binary_crossentropy, is specific to binary classification.

Training the Model
Once a neural network has been created, it is very easy to train it using Keras:

max_epochs = 500
my_logger = MyLogger(n=50)
h = model.fit(train_x, train_y, batch_size=32,
  epochs=max_epochs, verbose=0, callbacks=[my_logger])

One epoch in Keras is defined as touching all training items one time. The number of epochs to use is a hyperparameter. The demo uses a batch size of 32, which is called mini-batch training. Alternatives are a batch size of one, called online training, and a batch size equal to the size of the training set, called batch training. Deep neural networks can be very sensitive to the batch size so when training fails, this is one of the first hyperparameters to adjust.

Setting the verbose parameter to 0 suppresses all built-in progress messages during training, but because the my_logger object is passed to the callbacks parameter, custom progress messages will be displayed every 50 epochs. The demo captures the return object from fit(), which is a log of training history information, but doesn't use it. The demo program doesn't save the trained model but in most cases you'll want to do so. For example:

mp = ".\\Models\\banknote_model.h5"
model.save(mp)

This code would save the model using the default hierarchical data format, which you can think of as sort of like a binary XML. It is also possible to save check-point models during training using the custom callback mechanism.

Evaluating and Using the Trained Model
After training completes, the demo program evaluates the prediction accuracy of the model on the test dataset:

np.set_printoptions(precision=4, suppress=True)
eval_results = model.evaluate(test_x, test_y, verbose=0) 
print("\nLoss, accuracy on test data: ")
print("%0.4f %0.2f%%" % (eval_results[0], \
  eval_results[1]*100))

The evaluate() function returns a list where the first item is the overall loss on the test dataset, which in this case is the binary cross entropy error. The second item is the overall classification accuracy on the test data. The demo multiplies the accuracy value by 100 to get a percentage such as 90.12 percent rather than a proportion such as 0.9012. The accuracy of the trained model on the test data is a rough approximation of the accuracy you'd expect on new, previously unseen data.

Making a Prediction
In most practical scenarios, the whole point of building a binary classification model is to use it to make predictions:

inpts = np.array([[0.5, 0.5, 0.5, 0.5]], dtype=np.float32)
pred = model.predict(inpts)
print("\nPredicting authenticity for: ")
print(inpts)
print("Probability that class = 1 (fake):")
print(pred)

The four input values are set to 0.5 each. Recall that the training and test data were normalized using min-max, therefore any prediction must use min-max normalized values. Because the output layer node uses sigmoid activation, the single output node will hold a value between 0.0 and 1.0 which represents the probability that the item is the class encoded as 1 in the data (forgery). Put another way, if the prediction value is less than 0.5 then the prediction is class = 0 = "authentic," otherwise the prediction is class = 1 = "forgery."

Wrapping Up
The demo program presented in this article can be used as a template for most binary classification problems. You encode the two possible classes as 0 or 1. The encoding is arbitrary, but it's up to you to keep track of the meaning of each encoding value. The number of input nodes will depend on the number of predictor variables, but there will always be just one

• Get Code Download