The Data Science Lab
The LogBeta and LogGamma Functions Using C#
The .NET library (formerly called .NET Core) doesn't have built-in functions for classical statistics analyses. But it is possible to implement such functions from scratch. This article presents C# implementations of three of the most important classical statistics functions: the log-beta function, the log-gamma function and the regularized incomplete beta function.
The regularized incomplete beta function is usually written as Ix(a,b) or I(x; a,b). It is used for many problems, including statistical analysis of variance (ANOVA). The Ix(a,b) function calls the log-beta function. The log-beta function calls the log-gamma function.
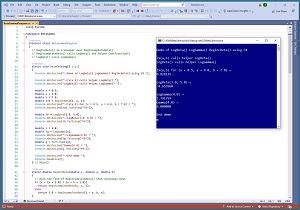 [Click on image for larger view.] Figure 1: Classical Statistics Functions Using C#
[Click on image for larger view.] Figure 1: Classical Statistics Functions Using C#
A good way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. The first part of the output shows the value of I(x; a, b) for x = 0.5, a = 4.0, b = 7.0, which is 0.828125. The regularized incomplete beta function has no obvious interpretation. It's best thought of as an abstract math function that accepts an x value between 0.0 and 1.0, and a and b values that are positive. The return value is a number between 0.0 and 1.0 which is why the function is called "regularized."
The second part of the output in Figure 1 shows the value of LogBeta(3.0, 5.0), which is -4.653960. Again, the function has no obvious interpretation and is best thought of as just a function that accepts two positive values. There is a plain Beta(a,b) function but the return value of Beta() can be very large and so it's standard practice to use LogBeta() which is literally the log of the Beta() function.
The third part of the output in Figure 1 shows the value of LogGamma(4.0), which is 6.0000. The plain Gamma() function is a generalization of the Factorial() function. If n is an integer, then Gamma(n) = Factorial(n-1). However, Gamma(z) is defined for positive real z. Because the return value of the Gamma(z) function can be astronomically large, it's standard practice to use LogGamma(z).
This article assumes you have intermediate or better programming skill with the C# language but doesn't assume you know anything about the beta, gamma or regularized incomplete beta functions. The complete demo code is presented in this article and is also available in the accompanying download. All normal error checking has been removed to keep the main ideas as clear as possible.
To create the demo program I used Visual Studio 2022 (the free Community edition) with .NET 5 (to avoid the annoying new .NET 6 Console template). However, the demo has no significant dependencies so any relatively recent versions of VS and .NET can be used.
The LogGamma() Function
The graph of the plain Gamma() function is shown in Figure 2. Notice that Gamma(n) = Factorial(n-1), for example, Gamma(4.0) = Factorial(3) = 3 * 2 * 1 = 6.0.
The LogGamma(z) function cannot be computed exactly when z is not an integer and so there are several approximation algorithms. The demo program uses what is called the Lanczos g=5, n=7 algorithm. The implementation is shown in Listing 1.
Listing 1: The LogGamma() Function
static double LogGamma(double z)
{
// Lanczos approximation g=5, n=7
double[] coef = new double[7] { 1.000000000190015,
76.18009172947146, -86.50532032941677,
24.01409824083091, -1.231739572450155,
0.1208650973866179e-2, -0.5395239384953e-5 };
double LogSqrtTwoPi = 0.91893853320467274178;
if (z < 0.5)
return Math.Log(Math.PI / Math.Sin(Math.PI * z)) -
LogGamma(1.0 - z);
double zz = z - 1.0;
double b = zz + 5.5; // g + 0.5
double sum = coef[0];
for (int i = 1; i < coef.Length; ++i)
sum += coef[i] / (zz + i);
return (LogSqrtTwoPi + Math.Log(sum) - b) +
(Math.Log(b) * (zz + 0.5));
}
The demo program calls the LogGamma() function using these statements:
double z = 4.0;
double lg = LogGamma(z);
Console.WriteLine("LogGamma(4.0) = ");
Console.WriteLine(lg.ToString("F6"));
double g = Math.Exp(lg);
Console.WriteLine("Gamma(4.0) = ");
Console.WriteLine(g.ToString("F6"));
The calculation of Gamma(4.0) by calling Math.Exp() on LogGamma(4.0) is done just to show that the LogGamma() function is just the log of the gamma function.
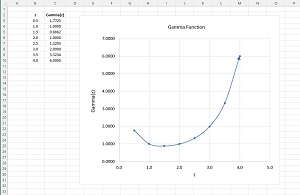 [Click on image for larger view.] Figure 2: Graph of the Plain Gamma() Function
[Click on image for larger view.] Figure 2: Graph of the Plain Gamma() Function
The demo doesn't do any error checking. In a non-demo scenario, you'd likely want to check the input parameter value to make sure it's positive.
The LogBeta() Function
The I(x; a, b) regularized incomplete beta function calls the LogBeta() function which in turn calls the LogGamma() function. The demo implementation of the LogBeta() function is:
static double LogBeta(double a, double b)
{
double logbeta = LogGamma(a) + LogGamma(b) -
LogGamma(a + b);
return logbeta;
}
The demo program calls the LogBeta() function like so:
double lb = LogBeta(3.0, 5.0);
Console.WriteLine("LogBeta(3.0, 5.0) = ");
Console.WriteLine(lb.ToString("F6"));
Mathematically, beta(a, b) = (gamma(a) * gamma(b)) / gamma(a + b). If you take the log() of both sides of the equation, and use the facts that log(x / y) = log(x) - log(y) and log(x * y) = log(x) + log(y) you get the result in the LogBeta() function implementation.
The Regularized Incomplete Beta Function
The I(x; a, b) regularized incomplete beta function is extremely tricky to implement. The demo program uses what is called the Continued Fractions (CF) approximation. The CF approximation equations are shown in Figure 3.
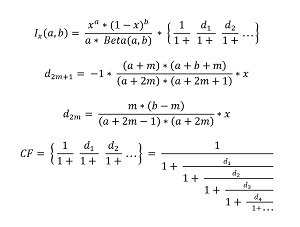 [Click on image for larger view.] Figure 3: Continued Fractions Approximation of the Regularized Incomplete Beta Function
[Click on image for larger view.] Figure 3: Continued Fractions Approximation of the Regularized Incomplete Beta Function
The I(x; a, b) CF approximation is the mathematical product of two main terms. The term on the left involves Beta(a, b). The term on the right has an infinite number of d[i] terms where the value of each term depends on whether [i] is even or odd. The demo implements the I(x; a, b) function as shown in Listing 2.
Listing 2: Regularized Incomplete Beta Function
static double RegIncBeta(double x, double a, double b)
{
// pick the form of RegIncompleteBeta() that converges best
if (x < (a + 1.0) / (a + b + 2.0))
return RegIncompleteBeta(x, a, b);
else
return 1.0 - RegIncompleteBeta(1 - x, b, a);
}
static double RegIncompleteBeta(double x, double a, double b)
{
// regularized incomplete beta
// calls LogBeta() and helper ContFraction()
double cf = ContFraction(x, a, b);
double logTop = (a * Math.Log(x)) +
(b * Math.Log(1 - x));
double logBot = Math.Log(a) + LogBeta(a, b);
double logLeft = logTop - logBot;
double left = Math.Exp(logLeft);
return left * cf; // should be [0.0, 1.0]
}
static double ContFraction(double x, double a, double b,
int maxTerms = 100)
{
// 1. pre-compute 100 d values
double[] d = new double[maxTerms]; // d[0] not used
int end = maxTerms / 2; // 50
for (int m = 0; m < end; ++m) // [0,49]
{
int i = 2 * m; // even di
int j = i + 1; // odd di
d[i] = (m * (b - m) * x) / ((a + 2 * m - 1) *
(a + 2 * m));
d[j] = -1 * ((a + m) * (a + b + m) * x) / ((a + 2 * m) *
(a + 2 * m + 1));
}
// 2. work backwards
double[] t = new double[maxTerms]; // t[0] not used
t[maxTerms - 1] = 1 + d[maxTerms - 1];
for (int j = maxTerms - 2; j >= 1; --j)
t[j] = 1 + d[j] / t[j + 1];
// ShowVector(t);
// Console.ReadLine();
double cf = 1 / t[1];
return cf;
}
There is a top-level RegIncBeta() function. It calls the RegIncompleteBeta() function that does all the work. The wrapper approach is based on the math property that I(x; a, b) = 1 - I(x-1; b, a) and it calls the version that converges more quickly. The RegIncompleteBeta() function calls a helper ContFraction() function that computes the CF term. To avoid calculating Beta(a, b), which can easily overflow, the RegIncompleteBeta() function computes LogBeta(a, b) and then undoes the log operation by calling the Math.Exp() function.
The demo program calls the I(x; a, b) function using these statements:
double x = 0.5;
double a = 4.0;
double b = 7.0;
double rib = RegIncBeta(x, a, b);
Console.WriteLine("Ix(a,b) for (x=0.5, a=4.0, b=7.0) = ");
Console.WriteLine(rib.ToString("F6"));
The ContFraction() helper function pre-computes 100 d[i] values and then computes the CF term working from the last d[i] value towards the first d[i] value. This approach could fail with numeric underflow or overflow for some combinations of x, a and b so in a non-demo scenario you'd likely want to wrap the code in a try-catch block.
Instead of using 100 pre-computed d[i] terms for the ContFraction() helper function, you could examine the value of the RegIncBeta() function, starting with maxTerms = 2 and increasing maxTerms until the RegIncBeta() function converges to a stable value. For example, with x = 0.5, a = 4.0, b = 7.0 the RegIncBeta() function stabilizes at maxTerms = 10:
maxTerms RegIncBeta()
=======================
2 0.812500
4 0.828613
6 0.828119
8 0.828125
10 0.828125
An alternative approach is to use what is called Lentz's algorithm to estimate the value of the CF term. Instead of pre-computing an arbitrary number of d[i] terms and then working backwards from the last d[i] value, Lentz's algorithm uses some clever math tricks to work forward, checking on each iteration to see if the CF value has converged to a stable value. However, Lentz's algorithm is often very brittle and for some problems doesn't converge.
Wrapping Up
There are many external code libraries that have implementations of complicated statistical functions such as beta, log-beta, gamma, log-gamma and regularized incomplete beta. For example, the scipy Python language library contains these functions. In many situations you can use such external libraries. However, implementing statistical functions from scratch using C# is useful when you want to avoid an external dependency for technical or copyright reasons.
About the Author
Dr. James McCaffrey works for Microsoft Research in Redmond, Wash. He has worked on several Microsoft products including Azure and Bing. James can be reached at [email protected].