The Data Science Lab
Neural Network Regression from Scratch Using C#
Compared to other regression techniques, a well-tuned neural network regression system can produce the most accurate prediction model, says Dr. James McCaffrey of Microsoft Research in presenting this full-code, step-by-step tutorial.
The goal of a machine learning regression problem is to predict a single numeric value. For example, you might want to predict the annual income of a person based on their sex (male or female), age, State of residence and political leaning (conservative, moderate, liberal).
There are roughly a dozen major regression techniques, and each technique has several variations. Among the most common techniques are linear regression, linear ridge regression, k-nearest neighbors regression, kernel ridge regression, Gaussian process regression, decision tree regression and neural network regression. Each technique has pros and cons. This article explains how to implement neural network regression from scratch, using the C# language.
Compared to other regression techniques, a well-tuned neural network regression system can produce the most accurate prediction model. However, neural networks are complex, sometimes don't work well with small (less than 100 items) datasets, and can be very difficult to tune.
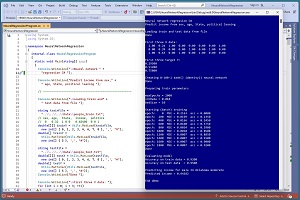
A good way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. The demo program uses a 200-item set of training data and a 40-item set of test data that look like:
0, 0.24, 1,0,0, 0.2950, 0,0,1
1, 0.39, 0,0,1, 0.5120, 0,1,0
0, 0.63, 0,1,0, 0.7580, 1,0,0
. . .
The fields are sex, age, State, income and political leaning. The goal is to predict income from the other four variables.
The demo program creates an 8-100-1 neural network regression model, which means there are 8 input nodes, 100 hidden processing nodes and 1 output node. The program trains the network for 2,000 epochs. The trained prediction model scores 0.9200 accuracy on the training data (184 out of 200 correct) and 0.9500 accuracy on a test dataset (38 out of 40 correct).
The demo program concludes by predicting the income for a new, previously unseen person who is male, age 34, lives in Oklahoma and is a political moderate. The predicted income is $44,382.
 [Click on image for larger view.] Figure 1: Neural Network Regression in Action
[Click on image for larger view.] Figure 1: Neural Network Regression in Action
This article assumes you have intermediate or better programming skill but doesn't assume you know anything about neural network regression. The demo is implemented using C#, but with a bit of effort you should be able to refactor the code to a different C-family language if you wish.
The source code for the demo program is too long to be presented in its entirety in this article. The complete code is available in the accompanying file download. The demo code and data are also available online.
Understanding the Data
To create a neural network regression system, the training data must be prepared by encoding categorical predictor variables and normalizing numeric predictor variables. For the demo, the raw data looks like:
F, 24, michigan, 29500.00, liberal
M, 39, oklahoma, 51200.00, moderate
F, 63, nebraska, 75800.00, conservative
M, 36, michigan, 44500.00, moderate
. . .
The normalized and encoded data looks like:
1, 0.24, 1, 0, 0, 0.2950, 0, 0, 1
0, 0.39, 0, 0, 1, 0.5120, 0, 1, 0
1, 0.63, 0, 1, 0, 0.7580, 1, 0, 0
0, 0.36, 1, 0, 0, 0.4450, 0, 1, 0
. . .
Binary predictors, such as sex (M, F), can be zero-one encoded or minus-one-plus-one encoded. In theory, minus-one-plus-one encoding is slightly superior to zero-one encoding, but in practice there is usually no significant difference. The demo uses zero-one encoding where male = 0 and female = 1.
Numeric predictor data should be normalized so that all values have roughly the same range. The three most common techniques for numeric normalization are divide-by-k, min-max and z-score. I recommend using the divide-by-k technique when possible. The age values are all divided by 100 so that the normalized age values are between 0 and 1. For regression problems, the target numeric variable can be normalized in the same way as predictor variables. The target income values are divided by 100,000 so they're all between 0 and 1.
Categorical predictor data should be one-hot encoded. The State predictor values are encoded so that Michigan = 100, Nebraska = 010 and Oklahoma = 001. If there were four State values, they would be encoded as 1000, 0100, 0010 and 0001. The political leaning values are encoded as conservative = 100, moderate = 010 and liberal = 001. The order in which categorical values are one-hot encoded is arbitrary.
The demo does not have ordinal predictor data such as a height variable with possible values short, medium and tall. In theory you can encode ordinal data using a scheme that retains order information, such as short = 0.3, medium = 0.5 and tall = 0.7, but in practice ordinal data is usually one-hot encoded.
Data normalization and encoding is a surprisingly complex and subtle topic. In a non-demo scenario, data preparation can be tedious and time-consuming. It is possible to use raw training and test data and then programmatically normalize and encode the data, but in practice, data is usually preprocessed.
Understanding Neural Network Regression
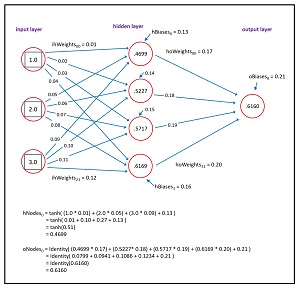
A neural network is essentially a complex math function. The neural network input-output mechanism is illustrated in Figure 2. The figure shows a simple neural network regression system with three input nodes, four hidden processing nodes, and one output node.
Each pair of nodes in adjacent layers is conceptually connected by a weight value. There are 3 * 4 = 12 input-to-hidden weights, and 4 * 1 = 4 hidden-to-output weights. Each hidden node and output node has a special weight called a bias, and so there are 4 + 1 = 5 bias values.
 [Click on image for larger view.] Figure 2: Neural Network Input-Output Mechanism
[Click on image for larger view.] Figure 2: Neural Network Input-Output Mechanism
The values of the hidden nodes are computed as the hyperbolic tangent (tanh) of the sum of the products of each input node times its weight, plus the bias. For example, to compute the value of the top-most hidden node, if the three input values are 1.0, 2.0 and 3.0, and the three associated input-to-hidden weights are 0.01, 0.05 and 0.09, and the bias value is 0.13, then:
hNode0 = tanh( (1.0 * 0.01) + (2.0 * 0.05) +
(3.0 * 0.09) + 0.13 )
= tanh( 0.01 + 0.10 + 0.27 + 0.13 )
= tanh(0.51)
= 0.4699
The tanh() function is called the hidden node activation. Other hidden node activation functions include logistic sigmoid (formerly quite common but now rarely used) and relu ("rectified linear unit"), which is most often used for very large neural networks with multiple hidden layers but is rarely used for neural regression systems.
The single output node is computed in the same way as each hidden node except that the activation function is identity() instead of tanh(). If the values of the four hidden nodes are (0.4699, 0.5227, 0.5717 and 0.6169) and the four associated hidden-to-output weights are (0.17, 0.18, 0.19 and 0.20), and the output node bias is 0.21, then the output node value is computed as:
oNode = identity( (0.4699 * 0.17) + (0.5227 * 0.18) +
(0.5717 * 0.19) + (0.6169 * 0.20) + 0.21 )
= identity( 0.0799 + 0.0941 + 0.1086 + 0.1234 + 0.21 )
= identity(0.6160)
= 0.6160
The identity() function just returns its input. For neural network classifiers that don't do regression, the most common output activation functions are softmax() for multi-class classification, and sigmoid() for binary classification.
To recap, a neural network regression system is a complex math function where the output value depends on the input values, the hidden layer activation function, the values of the input-hidden weights, the hidden biases, the hidden-output weights and the output bias. But where do the values of the weights and biases come from?
Neural network weights and biases are computed by looking at training data with known input values and known correct output values. The idea is to find values of the weights and biases so that computed output values are as close as possible to the target correct values. Put another way, the values of the weights and biases are those that minimize the error between computed and target values.
Although there are several algorithms to find the values of neural network weights and biases, by far the most common technique is called stochastic gradient descent (SGD). There are many variations of SGD including Adam (adaptive momentum), RMSProp (root mean squared resilient back-propagation) and others. The specific algorithm used for SGD is called back-propagation (often spelled without the hyphen).
Training a neural network is one of the most complex topics in machine learning -- even explaining the complexity of neural network training is complex. That said, you don't need to have a complete understanding of how neural network training works -- which would literally take months of dedicated study -- in order to use neural networks effectively. An analogy is that you don't need to have a complete understanding of internal combustion engines in order to use an automobile effectively.
Overall Program Structure
I used Visual Studio 2022 (Community Free Edition) for the demo program. I created a new C# console application named NeuralNetworkRegression and checked the "Place solution and project in the same directory" option. I specified .NET version 6.0. I checked the "Do not use top-level statements" option to avoid the program entry point shortcut syntax.
The demo program has no significant .NET dependencies and any relatively recent version of Visual Studio with .NET (Core) or the older .NET Framework will work fine. You can also use the Visual Studio Code program if you like.
After the template code loaded into the editor, I right-clicked on file Program.cs in the Solution Explorer window and renamed the file to the more descriptive NeuralRegressionProgram.cs. I allowed Visual Studio to automatically rename class Program.
The overall program structure is presented in Listing 1. The demo program has three primary classes. The Program class holds all the control logic. The NeuralNetwork class houses all the neural network functionality. The Utils class houses functionality to load data from file into memory.
Listing 1: Overall Program Structure
using System;
using System.IO;
namespace NeuralNetworkRegression
{
internal class NeuralRegressionProgram
{
static void Main(string[] args)
{
Console.WriteLine("Neural network " +
"regression C# ");
Console.WriteLine("Predict income from sex," +
" age, State, political leaning ");
// 1. load data from file into memory
// 2. create neural network
// 3. train neural network
// 3. evaluate neural network accuracy
// 4. use neural network to make a prediction
Console.WriteLine("End demo ");
Console.ReadLine();
} // Main
} // Program
public class NeuralNetwork
{
private int ni; // number input nodes
private int nh;
private int no;
private double[] iNodes;
private double[][] ihWeights; // input-hidden
private double[] hBiases;
private double[] hNodes;
private double[][] hoWeights; // hidden-output
private double[] oBiases;
private double[] oNodes; // single val as array
private Random rnd;
public NeuralNetwork(int numIn, int numHid,
int numOut, int seed) { . . }
private void InitWeights() { . . }
public void SetWeights(double[] wts) { . . }
public double[] GetWeights() { . . }
public double ComputeOutput(double[] x) { . . }
private static double HyperTan(double x) { . . }
private static double Identity(double x) { . . }
public void TrainBatch(double[][] trainX,
double[] trainY, double lrnRate, int batSize,
int maxEpochs) { . . }
private void Shuffle(int[] sequence) { . . }
public double Error(double[][] trainX,
double[] trainY) { . . }
public double Accuracy(double[][] dataX,
double[] dataY, double pctClose) { . . }
} // NeuralNetwork class
public class Utils
{
public static double[][] VecToMat(double[] vec,
int rows, int cols) { . . }
public static double[][] MatCreate(int rows,
int cols) { . . }
static int NumNonCommentLines(string fn,
string comment) { . . }
public static double[][] MatLoad(string fn,
int[] usecols, char sep, string comment) { . . }
public static double[] MatToVec(double[][] m) { . . }
public static void MatShow(double[][] m,
int dec, int wid) { . . }
public static void VecShow(int[] vec, int wid) { . . }
public static void VecShow(double[] vec,
int dec, int wid, bool newLine) { . . }
} // Utils class
} // ns
Creating the Neural Network Regression Model
The Main method begins by loading the 200-item training data from file into memory:
string trainFile =
"..\\..\\..\\Data\\people_train.txt";
// sex, age, State, income, politics
// 0 0.32 1 0 0 0.65400 0 0 1
double[][] trainX = Utils.MatLoad(trainFile,
new int[] { 0, 1, 2, 3, 4, 6, 7, 8 }, ',', "#");
double[] trainY =
Utils.MatToVec(Utils.MatLoad(trainFile,
new int[] { 5 }, ',', "#"));
The code assumes that the data file is in a directory named Data in the root project directory. The MatLoad() arguments instruct the method to load comma-separated columns 0, 1, 2, 3, 4, 6, 7 and 8 as predictors, where lines beginning with "#" are interpreted as comments. The income values in column 5 are loaded into a C# matrix and then converted to an array/vector.
The 40-item test data is loaded in the same way:
string testFile =
"..\\..\\..\\Data\\people_test.txt";
double[][] testX = Utils.MatLoad(testFile,
new int[] { 0, 1, 2, 3, 4, 6, 7, 8 }, ',', "#");
double[] testY =
Utils.MatToVec(Utils.MatLoad(testFile,
new int[] { 5 }, ',', "#"));
Next, the first three lines of predictor values and the corresponding target income values are displayed:
Console.WriteLine("First three X data: ");
for (int i = 0; i < 3; ++i)
Utils.VecShow(trainX[i], 2, 6, true);
Console.WriteLine("First three target Y: ");
for (int i = 0; i < 3; ++i)
Console.WriteLine(trainY[i].ToString("F5"));
In a non-demo scenario, you'd probably want to display all the training and test data to make sure it has been loaded correctly. Next, the neural network is created using this statement:
NeuralNetwork nn =
new NeuralNetwork(8, 100, 1, seed: 0);
The network has 8 input nodes, 100 hidden processing nodes and 1 output node. The number of input and output nodes is determined by the data. The number of hidden nodes is a hyperparameter that must be determined by trial and error. The seed parameter is fed to an internal C# Random generator object, which is used to randomly initialize the values of the network weights and biases, and to randomly shuffle the order of the training data during training.
Training the Neural Network Regression Model
The neural network training parameters are set like so:
int maxEpochs = 2000;
double lrnRate = 0.01;
int batSize = 10;
A training epoch is one pass through the training dataset. The max epochs value must be determined by trial and error. If you use too few training epochs, the resulting model will underfit and predict poorly. If you use too many training epochs, the model will overfit where prediction accuracy on the training data is high but accuracy on new, previously unseen data is low.
The learning rate controls how much the weight and bias values change on each training iteration. The learning rate must be determined by trial and error. If you use a rate that is too small, training will be too slow. If you use a rate that is too high, training can jump past good weight and bias values.
The batch size controls how many training items are analyzed to estimate the overall error gradient before weights and biases are updated. It is good practice to use a batch size that evenly divides the number of training items so that all batches have the same number of data items.
The neural network is trained using these statements:
Console.WriteLine("Starting (batch) training ");
nn.TrainBatch(trainX, trainY, lrnRate,
batSize, maxEpochs);
Console.WriteLine("Done ");
The max epochs, learning rate and batch size interact in complex ways, and so when you search for good values, it's not possible to optimize each parameter in a sequential way. Searching for good training parameter values is often time-consuming. Typically, my colleagues and I begin by manually searching for good combinations of values. Once we get a rough idea of what the ranges of good values might be, we set up arrays of possible values and then programmatically try all possible combinations. This is called grid search.
Evaluating the Neural Network Regression Model
During training, the neural network is monitored by computing and displaying the mean squared error between computed output values and correct target values. For example, with just three data items, if the correct target income values are (0.5000, 0.9200 and 0.6800) and the associated predicted income values are (0.4800, 0.9600 and 0.6700), then the mean squared error is ((0.5000 - 0.4800)^2 + (0.9200 - 0.9600)^2 + (0.6800 - 0.6700)^2) / 3 = (0.0004 + 0.0016 + 0.0001) / 3 = 0.0007. A common alternative, which has the same amount of information, is root mean squared error, which is just the square root of mean squared error.
Because there is no inherent definition of regression model accuracy, it's necessary to implement a program-defined accuracy method. The demo network defines a correct prediction as one that is within a specified percentage of the true target income value. The demo uses 10 percent, but a reasonable percentage interval to use will vary from problem to problem. The calling statements are:
double trainAcc = nn.Accuracy(trainX, trainY, 0.10);
Console.WriteLine("Accuracy on train data = " +
trainAcc.ToString("F4"));
double testAcc = nn.Accuracy(testX, testY, 0.10);
Console.WriteLine("Accuracy on test data = " +
testAcc.ToString("F4"));
Model accuracy is ultimately what you're after in most situations. But accuracy is too coarse to use for training. Mean squared error is less ambiguous than accuracy but can be misleading when evaluating a regression model.
Using the Neural Network Regression Model
After the neural network model has been evaluated, the demo concludes by using the model to predict the income of a previously unseen person who is male, age 34, lives in Oklahoma and is a political moderate:
Console.WriteLine("Predicting income for male" +
" 34 Oklahoma moderate ");
double[] X = new double[] { 0, 0.34, 0,0,1, 0,1,0 };
double y = nn.ComputeOutput(X);
Console.WriteLine("Predicted income = " +
y.ToString("F5"));
Console.WriteLine("End demo ");
Console.ReadLine(); // keep shell open
Predictions must be made using the same encoding and normalization that's used when training the model. The output of 0.44382 is normalized so the actual predicted income is $44,382.
In a non-demo scenario, you might want to save the trained model weights and biases so that the model can be used without retraining it. Saving would look like:
string fn = "..\\..\\..\\Models\\people_wts.txt";
nn.SaveWeights(fn);
Then another system could use the trained model like so:
string fn = "..\\..\\..\\Models\\people_wts.txt";
NeuralNetwork nn2 = new NeuralNetwork(8, 100, 1, 0);
nn2.LoadWeights(fn);
Notice that this approach assumes the system that uses the trained model has access to the NeuralNetwork class definition.
Wrapping Up
The demo program can be used as a template for most regression problems. The architecture parameter to explore is the number of hidden nodes. The training hyperparameters to explore are the max epochs, learning rate, and batch size.
The demo program uses random uniform initialization for the network weights and biases. The key code is:
double lo = -0.01; double hi = +0.01;
int numWts = (this.ni * this.nh) +
(this.nh * this.no) + this.nh + this.no;
double[] initialWeights = new double[numWts];
for (int i = 0; i < initialWeights.Length; ++i)
initialWeights[i] =
(hi - lo) * rnd.NextDouble() + lo;
The range is specified as [-0.01, +0.01). Somewhat surprisingly, weight and bias initialization values have a big impact on a neural network model. You might want to experiment with other initialization range values, however this introduces two more hyperparameters to deal with. Large neural networks often use fancy initialization schemes based on the neural architecture -- Glorot initialization, He initialization and others -- but these can be a bit of overkill for relatively simple neural networks like the one presented in this article.
The demo neural network uses a single hidden layer. It is possible to extend the demo network architecture to multiple hidden layers, but this requires a huge effort. Theoretically, a neural network with a single hidden layer and enough hidden nodes can compute anything that a neural network with multiple hidden layers can compute. This fact comes from what is called the Universal Approximation Theorem.
The demo uses tanh() hidden node activation and identity() output node activation. The training method assumes these two activation functions are used, so you shouldn't change activation functions unless you understand the deep theory of back-propagation and can modify the training code.
Note: My thanks to Thorsten Kleppe who reviewed the code presented in this article and made valuable suggestions.