The Data Science Lab
Matrix Inverse from Scratch Using SVD Decomposition with C#
Dr. James McCaffrey of Microsoft Research presents a full-code, step-by-step tutorial on an implementation of the technique that emphasizes simplicity and ease-of-modification over robustness and performance.
Computing the inverse of a matrix is one of the most important operations in machine learning. If some matrix A has shape n-by-n, then its inverse matrix Ai is n-by-n and the matrix product of Ai * A is the n-by-n Identity matrix (1s on the upper-left to lower-right main diagonal, 0s off the diagonal).
An analogy in ordinary arithmetic is that for a number n, its inverse ni is a number such that n * ni = 1. For example, the inverse of 4 is 0.25 because 4 * 0.25 = 1.
There are several algorithms to compute a matrix inverse, and each algorithm has several variations. Three common algorithms are LUP ("lower upper permutation"), SVD ("singular value decomposition") and QR (not an acronym). This article presents a from-scratch C# language implementation of matrix inverse using the Jacobi version of the SVD algorithm. Other versions of the SVD algorithm include Householder, Golub-Reinsch, Demmel-Kahan, bisection and divide-and-conquer.
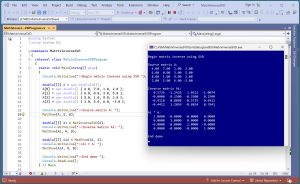 [Click on image for larger view.] Figure 1: Matrix Inverse Via QR Decomposition In Action
[Click on image for larger view.] Figure 1: Matrix Inverse Via QR Decomposition In Action
There are pros and cons of each matrix inverse algorithm. In the early days of programming, when machines had limited memory and slow processors, the practical differences between matrix inverse algorithms were far more important than they are today. In my subjective opinion, SVD-Jacobi matrix inversion has high complexity, high stability and medium efficiency.
A good way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. For simplicity, the demo sets up a small 4-by-4 matrix A:
4.00 7.00 1.00 2.00
6.00 0.00 3.00 5.00
8.00 1.00 9.00 2.00
2.00 5.00 6.00 -3.00
The demo computes the inverse Ai:
0.5735 -1.2426 1.0221 -1.0074
-0.0000 0.2500 -0.2500 0.2500
-0.4118 0.8088 -0.5735 0.6912
-0.4412 1.2059 -0.8824 0.7941
The demo concludes by computing Ai * A to verify the result is the Identity matrix:
1.0000 -0.0000 -0.0000 0.0000
0.0000 1.0000 0.0000 0.0000
-0.0000 0.0000 1.0000 -0.0000
0.0000 -0.0000 -0.0000 1.0000
The six -0.0000 values indicate that the value is a very small negative number (truncated for display), not a special negative-zero value of some sort.
This article assumes you have intermediate or better programming skill but doesn't assume you know anything about the SVD-Jacobi matrix inverse algorithm. The demo is implemented using C#, but you should be able to refactor the demo code to another C-family language if you wish.
The source code for the demo program is long but is presented in this article. The complete code is also available in the accompanying file download and online. The demo code has all normal error checking removed to keep the main ideas as clear as possible.
The Demo Program
I used Visual Studio 2022 (Community Free Edition) for the demo program. I created a new C# console application and checked the "Place solution and project in the same directory" option. I specified .NET version 8.0. I named the project MatrixInverseSVD. I checked the "Do not use top-level statements" option to avoid the program entry point shortcut syntax.
The demo has no significant .NET dependencies, and any relatively recent version of Visual Studio with .NET (Core) or the older .NET Framework will work fine. You can also use the Visual Studio Code program if you like.
After the template code loaded into the editor, I right-clicked on file Program.cs in the Solution Explorer window and renamed the file to the slightly more descriptive MatrixInverseSVDProgram.cs. I allowed Visual Studio to automatically rename class Program.
The Main() method starts by loading and displaying a 4-by-4 matrix into memory as an array-of-arrays style matrix:
double[][] A = new double[4][];
A[0] = new double[] { 4.0, 7.0, 1.0, 2.0 };
A[1] = new double[] { 6.0, 0.0, 3.0, 5.0 };
A[2] = new double[] { 8.0, 1.0, 9.0, 2.0 };
A[3] = new double[] { 2.0, 5.0, 6.0, -3.0 };
Console.WriteLine("Source matrix A: ");
MatShow(A, 2, 6);
The MatShow() function is a program-defined helper. The two numeric arguments are the number of decimals to display (2) and the field width (6) for each element. For simplicity, the data is hard-coded. In a non-demo scenario, the source matrix may come from some other part of a software system, or you might load the data from a text file using a program-defined helper function:
string fn = "..\\..\\..\\Data\\source_data.txt";
double[][] X = MatLoad(fn, new int[] { 0, 1, 2, 3 },
',', "#");
The arguments to MatLoad() mean fetch columns 0 through 3 of the comma-separated data, where a "#" character indicates a comment line.
The inverse is computed and displayed like so:
double[][] Ai = MatInverseSVD(A);
Console.WriteLine("Inverse matrix Ai: ");
MatShow(Ai, 4, 9);
Because the inverse function is implemented from scratch, you'll be able to modify it in many ways to meet your own needs. For example, you might want to also return the absolute value of the determinant of the matrix argument as an out parameter:
double absDet;
double[][] Ai = MatInverseSVD(A, out absDet);
The demo program concludes by verifying Ai * A equals the Identity matrix:
double[][] AiA = MatProd(Ai, A);
Console.WriteLine("Ai * A: ");
MatShow(AiA, 4, 9);
A more robust verification would also compute A * Ai, and programmatically check that the product has 1s on the diagonal and 0s off-diagonal, subject to a small error.
Understanding SVD Decomposition
The MatInverseSVD() function is based on SVD decomposition. If you have an n-by-n matrix A and apply SVD decomposition, the result has three components: an n-by-n matrix U, an n-dim vector s and an n-by-n matrix Vh, such that U * S * Vh = A, where S is an n-by-n matrix that has the values of the s vector on the diagonal. For example, if s = [2.5, -0.3, 1.7, 0.4] then S =
2.5 0.0 0.0 0.0
0.0 -0.3 0.0 0.0
0.0 0.0 1.7 0.0
0.0 0.0 0.0 0.4
The U matrix is special because its inverse equals the transpose of U (rows and columns exchanged). The S matrix is special because it is diagonal and so its inverse is easy to compute -- just invert the diagonal elements. The Vh matrix (sometimes named Vt) is special because its inverse equals the transpose of Vh.
To compute the inverse of a matrix A = U * S * Vh, the math derivation is:
A = U * S * Vh
inv(A) = inv(U * S * Vh)
= inv(Vh) * inv(S) * inv(Vh)
= trans(Vh) * inv(S) * trans(U)
The implementation of the MatInverseSVD() function is deceptively simple looking:
static double[][] MatInverseSVD(double[][] M)
{
double[][] U; double[][] Vh; double[] s;
MatDecomposeSVD(M, out U, out Vh, out s);
double[][] Sinv = MatInvFromVec(s);
double[][] V = MatTranspose(Vh);
double[][] Utrans = MatTranspose(U);
double[][] result = MatProduct(V,
MatProduct(Sinv, Utrans));
return result;
// 11 nested helper functions go here
}
Ten of the 11 helper functions are relatively simple, but the MatDecomposeSVD() function is very complicated.
Not all matrices have an inverse. A common customization is to check if the inverse of the source matrix does not exist. This happens when the determinant of the source matrix is 0. The determinant is 0 when any element of the s vector is 0, or equivalently, if the product of the elements of s is 0.
For example, you can add code similar to this:
double absDet = 1.0;
for (int i = 0; i < M.Length; ++i)
absDet *= s[i];
if (absDet == 0.0)
Console.WriteLine("Inverse does not exist ");
The product of the elements of s is the absolute value of the determinant of the source matrix, and so SVD decomposition cannot be used to compute the determinant. But you can check if the determinant is 0 or not.
The Jacobi method for singular value decomposition is not at all obvious. The Wikipedia entry on "Jacobi eigenvalue algorithm" has an explanation and a worked example.
The Complete Demo Program
The structure of the demo program is presented in Listing 1. The MatInverseSVD() contains 11 nested helper functions. The MatProd() function is used to compute Ai * A to verify the inverse result is correct. The MatLoad() function isn't called by the demo but is useful in non-demo scenarios.
Listing 1: Structure of the Demo Program
using System;
using System.IO;
namespace MatrixInverseSVD
{
internal class MatrixInverseSVDProgram
{
static void Main(string[] args)
{
Console.WriteLine("Begin matrix inverse using SVD ");
// set up and display a matrix A
// compute and display the inverse Ai
// compute and display Ai * A
Console.WriteLine("End demo ");
Console.ReadLine();
} // Main
static double[][] MatProd(double[][] matA,
double[][] matB) { . . }
static double[][] MatInverseSVD(double[][] M) { . . }
static void MatShow(double[][] M, int dec,
int wid) { . . }
static double[][] MatLoad(string fn, int[] usecols,
char sep, string comment) { . . }
} // Program
} // ns
The code for the MatInverseSVD() function is presented in Listing 2. The code for the MatDecomposeSVD() helper function assumes that the source matrix is square because the helper is being used to compute a matrix inverse and inverse only applies to square matrices. There are other versions of SVD decomposition functions that work for non-square matrices.
Listing 2: The MatInverseSVD Function
using System;
using System.IO;
namespace MatrixInverseSVD
{
internal class MatrixInverseSVDProgram
{
static void Main(string[] args)
{
Console.WriteLine("\nMatrix inverse using SVD ");
double[][] A = new double[4][];
A[0] = new double[] { 4.0, 7.0, 1.0, 2.0 };
A[1] = new double[] { 6.0, 0.0, 3.0, 5.0 };
A[2] = new double[] { 8.0, 1.0, 9.0, 2.0 };
A[3] = new double[] { 2.0, 5.0, 6.0, -3.0 };
Console.WriteLine("\nSource matrix A: ");
MatShow(A, 2, 6);
double[][] Ai = MatInverseSVD(A);
Console.WriteLine("\nInverse matrix Ai: ");
MatShow(Ai, 4, 9);
double[][] AiA = MatProd(Ai, A);
Console.WriteLine("\nAi * A: ");
MatShow(AiA, 4, 9);
Console.WriteLine("\nEnd demo ");
Console.ReadLine();
} // Main
static double[][] MatProd(double[][] matA,
double[][] matB)
{
int aRows = matA.Length;
int aCols = matA[0].Length;
int bRows = matB.Length;
int bCols = matB[0].Length;
if (aCols != bRows)
throw new Exception("Non-conformable matrices");
//double[][] result = MatMake(aRows, bCols);
double[][] result = new double[aRows][];
for (int i = 0; i < aRows; ++i)
result[i] = new double[bCols];
for (int i = 0; i < aRows; ++i) // each row of A
for (int j = 0; j < bCols; ++j) // each col of B
for (int k = 0; k < aCols; ++k)
result[i][j] += matA[i][k] * matB[k][j];
return result;
}
// ======================================================
static double[][] MatInverseSVD(double[][] M)
{
// SVD Jacobi algorithm
// A = U * S * Vh
// inv(A) = tr(Vh) * inv(S) * tr(U)
double[][] U;
double[][] Vh;
double[] s;
MatDecomposeSVD(M, out U, out Vh, out s);
// TODO: check if determinant is zero (no inverse)
// double absDet = 1.0;
// for (int i = 0; i < M.Length; ++i)
// absDet *= s[i];
// Console.WriteLine(absDet); Console.ReadLine();
// convert s vector to Sinv matrix
double[][] Sinv = MatInvFromVec(s);
double[][] V = MatTranspose(Vh);
double[][] Utrans = MatTranspose(U);
double[][] result = MatProduct(V,
MatProduct(Sinv, Utrans));
return result;
// ----------------------------------------------------
// 11 helpers: MatDecomposeSVD, MatMake, MatCopy,
// MatIdentity, MatGetColumn, MatTranspose,
// MatInvFromVec, MatProduct, VecNorm, VecDot, Hypot
// ----------------------------------------------------
static void MatDecomposeSVD(double[][] mat,
out double[][] U, out double[][] Vh,
out double[] s)
{
// assumes source matrix is square
double EPSILON = 1.0e-15;
double[][] A = MatCopy(mat); // working U
int m = A.Length;
int n = A[0].Length; // check m == n
double[][] Q = MatIdentity(n); // working V
double[] t = new double[n]; // working s
int ct = 1; // rotation counter
int pass = 0;
double tol = 10 * n * EPSILON; // heuristic
int passMax = 5 * n;
if (passMax < 15) passMax = 15; // heuristic
// save the column error estimates
for (int j = 0; j < n; ++j)
{
double[] cj = MatGetColumn(A, j);
double sj = VecNorm(cj);
t[j] = EPSILON * sj;
}
while (ct > 0 && pass <= passMax)
{
ct = n * (n - 1) / 2; // rotation counter
for (int j = 0; j < n - 1; ++j)
{
for (int k = j + 1; k < n; ++k)
{
double sin; double cos;
double[] cj = MatGetColumn(A, j);
double[] ck = MatGetColumn(A, k);
double p = 2.0 * VecDot(cj, ck);
double a = VecNorm(cj);
double b = VecNorm(ck);
double q = a * a - b * b;
double v = Hypot(p, q);
double errorA = t[j];
double errorB = t[k];
bool sorted = false;
if (a >= b) sorted = true;
bool orthog = false;
if (Math.Abs(p) <=
tol * (a * b)) orthog = true;
bool badA = false;
if (a < errorA) badA = true;
bool badB = false;
if (b < errorB) badB = true;
if (sorted == true && (orthog == true ||
badA == true || badB == true))
{
--ct;
continue;
}
// compute rotation angles
if (v == 0 || sorted == false)
{
cos = 0.0;
sin = 1.0;
}
else
{
cos = Math.Sqrt((v + q) / (2.0 * v));
sin = p / (2.0 * v * cos);
}
// apply rotation to A (U)
for (int i = 0; i < m; ++i)
{
double Aik = A[i][k];
double Aij = A[i][j];
A[i][j] = Aij * cos + Aik * sin;
A[i][k] = -Aij * sin + Aik * cos;
}
// update singular values
t[j] = Math.Abs(cos) * errorA +
Math.Abs(sin) * errorB;
t[k] = Math.Abs(sin) * errorA +
Math.Abs(cos) * errorB;
// apply rotation to Q (V)
for (int i = 0; i < n; ++i)
{
double Qij = Q[i][j];
double Qik = Q[i][k];
Q[i][j] = Qij * cos + Qik * sin;
Q[i][k] = -Qij * sin + Qik * cos;
} // i
} // k
} // j
++pass;
} // while
// compute singular values
double prevNorm = -1.0;
for (int j = 0; j < n; ++j)
{
double[] column = MatGetColumn(A, j);
double norm = VecNorm(column);
// check if singular value is zero
if (norm == 0.0 || prevNorm == 0.0
|| (j > 0 && norm <= tol * prevNorm))
{
t[j] = 0.0;
for (int i = 0; i < m; ++i)
A[i][j] = 0.0;
prevNorm = 0.0;
}
else
{
t[j] = norm;
for (int i = 0; i < m; ++i)
A[i][j] = A[i][j] * 1.0 / norm;
prevNorm = norm;
}
}
if (ct > 0)
{
Console.WriteLine("Jacobi iterations did not" +
" converge");
}
U = A;
Vh = MatTranspose(Q);
s = t;
// to sync with default np.linalg.svd() shapes:
// if m < n, extract 1st m columns of U
// extract 1st m values of s
// extract 1st m rows of Vh
// not applicable for matrix inverse.
// if (m < n)
// {
// U = MatExtractFirstColumns(U, m);
// s = VecExtractFirst(s, m);
// Vh = MatExtractFirstRows(Vh, m);
// }
} // MatDecomposeSVD
static double[][] MatMake(int r, int c)
{
double[][] result = new double[r][];
for (int i = 0; i < r; ++i)
result[i] = new double[c];
return result;
}
static double[][] MatCopy(double[][] m)
{
int r = m.Length; int c = m[0].Length;
double[][] result = MatMake(r, c);
for (int i = 0; i < r; ++i)
for (int j = 0; j < c; ++j)
result[i][j] = m[i][j];
return result;
}
static double[][] MatIdentity(int n)
{
double[][] result = MatMake(n, n);
for (int i = 0; i < n; ++i)
result[i][i] = 1.0;
return result;
}
static double[] MatGetColumn(double[][] m, int j)
{
int rows = m.Length;
double[] result = new double[rows];
for (int i = 0; i < rows; ++i)
result[i] = m[i][j];
return result;
}
static double[][] MatTranspose(double[][] m)
{
int r = m.Length;
int c = m[0].Length;
double[][] result = MatMake(c, r);
for (int i = 0; i < r; ++i)
for (int j = 0; j < c; ++j)
result[j][i] = m[i][j];
return result;
}
static double[][] MatInvFromVec(double[] s)
{
// Sinv from s
int n = s.Length;
double[][] result = MatMake(n, n);
for (int i = 0; i < n; ++i)
result[i][i] = 1.0 / s[i];
return result;
}
static double[][] MatProduct(double[][] matA,
double[][] matB)
{
int aRows = matA.Length;
int aCols = matA[0].Length;
int bRows = matB.Length;
int bCols = matB[0].Length;
if (aCols != bRows)
throw new Exception("Non-conformable matrices");
double[][] result = MatMake(aRows, bCols);
for (int i = 0; i < aRows; ++i)
for (int j = 0; j < bCols; ++j)
for (int k = 0; k < aCols; ++k)
result[i][j] += matA[i][k] * matB[k][j];
return result;
}
static double VecNorm(double[] vec)
{
double sum = 0.0;
int n = vec.Length;
for (int i = 0; i < n; ++i)
sum += vec[i] * vec[i];
return Math.Sqrt(sum);
}
static double VecDot(double[] v1, double[] v2)
{
int n = v1.Length;
double sum = 0.0;
for (int i = 0; i < n; ++i)
sum += v1[i] * v2[i];
return sum;
}
static double Hypot(double x, double y)
{
// fancy sqrt(x^2 + y^2)
double xabs = Math.Abs(x);
double yabs = Math.Abs(y);
double min, max;
if (xabs < yabs)
{
min = xabs; max = yabs;
}
else
{
min = yabs; max = xabs;
}
if (min == 0)
return max;
double u = min / max;
return max * Math.Sqrt(1 + u * u);
}
} // MatInverseSVD
// ======================================================
static void MatShow(double[][] M, int dec, int wid)
{
for (int i = 0; i < M.Length; ++i)
{
for (int j = 0; j < M[0].Length; ++j)
{
double v = M[i][j];
Console.Write(v.ToString("F" + dec).
PadLeft(wid));
}
Console.WriteLine("");
}
}
static double[][] MatLoad(string fn, int[] usecols,
char sep, string comment)
{
// self-contained version
// first, count number of non-comment lines
int nRows = 0;
string line = "";
FileStream ifs = new FileStream(fn, FileMode.Open);
StreamReader sr = new StreamReader(ifs);
while ((line = sr.ReadLine()) != null)
if (line.StartsWith(comment) == false)
++nRows;
sr.Close(); ifs.Close();
int nCols = usecols.Length;
double[][] result = new double[nRows][];
for (int r = 0; r < nRows; ++r)
result[r] = new double[nCols];
line = "";
string[] tokens = null;
ifs = new FileStream(fn, FileMode.Open);
sr = new StreamReader(ifs);
int i = 0;
while ((line = sr.ReadLine()) != null)
{
if (line.StartsWith(comment) == true)
continue;
tokens = line.Split(sep);
for (int j = 0; j < nCols; ++j)
{
int k = usecols[j]; // into tokens
result[i][j] = double.Parse(tokens[k]);
}
++i;
}
sr.Close(); ifs.Close();
return result;
}
} // Program
} // ns
The Helper Functions
The purpose of most of the 11 helper functions should be clear from their names or by examining the source code. The Hypot(x, y) function computes sqrt(x^2 + y^2) in a clever way that avoids arithmetic overflow and underflow errors. The VecNorm(v) function computes the norm() of a vector, which is the square root of the sum of the squared elements of vector v. The VecDot(v1, v2) function computes the dot product of vectors v1 and v2, which is the sum of the products of corresponding elements of v1 and v2.
The special MatInvFromVec(s) is used to convert a vector s to a diagonal matrix S and then to the inverse of S. For example, if s = (4.00, 0.20, 1.00) then S =
4.00 0.00 0.00
0.00 0.20 0.00
0.00 0.00 1.00
and then the inverse of S =
0.25 0.00 0.00
0.00 5.00 0.00
0.00 0.00 1.00
An alternative design is to define a separate MatFromVec() function and a MatInvDiag() function.
Wrapping Up
Inverting a matrix using SVD decomposition is a good, general-purpose approach. For special types of matrices, there are different algorithms that are more efficient. If the source matrix is 3-by-3 or smaller, then it's possible to compute the inverse using brute force. If you need the determinant of the source matrix, then using LUP decomposition (Crout or Doolittle algorithm) is useful. If the source matrix is a covariance matrix, then using Cholesky decomposition is more efficient.
The implementation of SVD-Jacobi matrix inverse presented in this article emphasizes simplicity and ease-of-modification over robustness and performance. Computing the inverse of a matrix, regardless of the algorithm used, can fail in many ways and so in a production system you must add lots of error checking.
It's not feasible to list all the machine learning algorithms that use matrix inverses -- there are just too many. That said however, examples of ML algorithms that use a matrix inverse are linear regression, logistic regression, Gaussian mixture model clustering, Gaussian process regression and kernel ridge regression.