The Data Science Lab
Principal Component Analysis from Scratch Using Singular Value Decomposition with C#
Dr. James McCaffrey of Microsoft Research presents a full-code, step-by-step tutorial on a classical ML technique that transforms a dataset into one with fewer columns, useful for creating a graph of data that has more than two columns, for example.
Principal component analysis (PCA) is a classical machine learning technique. The goal of PCA is to transform a dataset into one with fewer columns. This is called dimensionality reduction. The transformed data can be used for visualization or as the basis for prediction using machine learning techniques that can't deal with a large number of predictor columns.
There are two main techniques to implement PCA. The first technique, sometimes called classical, computes eigenvalues and eigenvectors from a covariance matrix derived from the source data. The second PCA technique sidesteps the covariance matrix and computes a singular value decomposition (SVD) of the (standardized) source data. Both techniques give the same results, subject to small error.
This article presents a from-scratch C# implementation of the second technique: using SVD to compute eigenvalues and eigenvectors from the standardized source data. If you're not familiar with PCA, most of the terminology -- covariance matrix, eigenvalues and eigenvectors and so on -- sounds quite mysterious. But the ideas will become clear shortly.
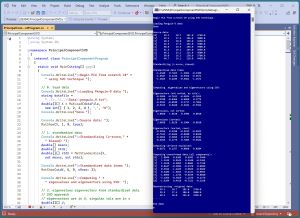[Click on image for larger view.] Figure 1: Demo Program of PCA Using SVD in Action
A good way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. For simplicity, the demo uses just nine data items:
[0] 39.1 18.7 181.0 3750.0
[1] 39.5 17.4 186.0 3800.0
[2] 40.3 18.0 195.0 3250.0
[3] 46.5 17.9 192.0 3500.0
[4] 50.0 19.5 196.0 3900.0
[5] 51.3 19.2 193.0 3650.0
[6] 46.1 13.2 211.0 4500.0
[7] 50.0 16.3 230.0 5700.0
[8] 48.7 14.1 210.0 4450.0
The nine data items are a small subset of the 333-item Penguin Dataset. Each line represents a penguin. The four columns are bill length, bill depth, flipper length and body mass. Because there are four columns, the data is said to have dimension = 4.
The leading index values in brackets are not part of the data. Each data item is one of three penguin species: 0 = Adelie, 1 = Chinstrap, 2 = Gentoo. The first three items are Adelie, the second three items are Chinstrap, and the last three items are Gentoo. The species labels were removed because they're not used for PCA dimensionality reduction.
PCA is intended for use with strictly numeric data. Mathematically, the technique works with Boolean variables (0-1 encoded) and for one-hot encoded categorical data. But conceptually, applying PCA to non-numeric data is questionable.
The demo program applies z-score normalization to the source data. Next, four eigenvalues and four eigenvectors are computed from the standardized data, using singular value decomposition. Then, the demo uses the eigenvectors to compute transformed data:
[0] 1.8846 0.6205 0.6592 -0.3440
[1] 1.3345 0.9543 0.3440 -0.2363
[2] 1.4610 0.5893 0.0603 0.7158
[3] 0.8447 -0.3894 -0.4378 0.0696
[4] 0.3924 -1.4465 0.0569 -0.0469
[5] 0.5486 -1.5813 -0.4221 -0.0953
[6] -1.6896 1.1743 -0.6539 -0.0640
[7] -3.1366 -0.3829 1.1156 0.1179
[8] -1.6394 0.4616 -0.7222 -0.1168
At this point, in a non-demo scenario, you could extract the first two or first three of the columns of the transformed data to use as a surrogate for the source data. For example, if you used the first two columns, you could graph the data with the first column acting as x-values and the second column acting as y-values.
The demo program concludes by programmatically reconstructing the source data from the transformed data. The idea is to verify the PCA worked correctly and also to illustrate that the transformed data contains all of the information in the source data.
This article assumes you have intermediate or better programming skill but doesn't assume you know anything about PCA. The demo is implemented using C#, but you should be able to refactor the demo code to another C-family language if you wish. All normal error checking has been removed to keep the main ideas as clear as possible.
The source code for the demo program is too long to be presented in its entirety in this article. The complete code is available in the accompanying file download, and is also available online.
Understanding Principal Component Analysis
The best way to understand PCA is to take a closer look at the demo program. The demo has eight steps:
- Load data into memory
- Normalize the data
- Apply singular value decomposition to the normalized data
- Compute eigenvalues and eigenvectors from the SVD results
- Sort the eigenvectors based on eigenvalues
- Compute variance explained by each eigenvector
- Use eigenvectors to compute transformed data
- Verify by reconstructing source data
The demo loads the source data using a helper MatLoad() function:
Console.WriteLine("Loading Penguin-9 data ");
string dataFile = "..\\..\\..\\Data\\penguin_9.txt";
double[][] X = MatLoad(dataFile, new int[] { 1,2,3,4 },
',', "#");
Console.WriteLine("Source data: ");
MatShow(X, 1, 9, true);
The arguments to MatLoad() mean fetch columns 1,2,3,4 of the comma-separated data, where a "#" character indicates a comment line. Column 0 of the data file has the species labels which aren't used. The arguments to MatShow() mean display using 1 decimal, with a field width of 9 per element, and display indices.
Normalizing the Data
Each column of the data is normalized using these statements:
Console.WriteLine("Standardizing (z-score, biased) ");
double[] means;
double[] stds;
double[][] stdX = MatStandardize(X, out means, out stds);
Console.WriteLine("Standardized data items ");
MatShow(stdX, 4, 9, nRows: 3);
The means and standard deviations for each of the four columns are saved because they are needed to reconstruct the original source data. The terms standardization and normalization are technically different but are often used interchangeably. Standardization is a specific type of normalization (z-score). PCA documentation tends to use the term standardization, but I often use the more general term, normalization.
Each value is normalized using the formula x' = (x - u) / s, where x' is the normalized value, x is the original value, u is the column mean and s is the column biased standard deviation (divide sum of squares by n rather than n-1 where n is the number of values in the column).
For example, suppose a column of some data has just n = 3 values: (4, 15, 8). The mean of the column is (4 + 15 + 8) / 3 = 9.0. The biased standard deviation of the column is sqrt( ((4 - 9.0)^2 + (15 - 9.0)^2 + (8 - 9.0)^2) / n) ) = sqrt( (25.0 + 36.0 + 1.0) / 3 ) = sqrt(62.0 / 3) = 4.55.
The normalized values for (4, 15, 8) are:
4: (4 - 9.0) / 4.55 = -1.10
15: (15 - 9.0) / 4.55 = 1.32
8: (8 - 9.0) / 4.55 = -0.22
Normalized values that are negative are less than the column mean, and normalized values that are positive are greater than the mean. For the demo data, the normalized data is:
-1.4440 0.7463 -1.2864 -0.4389
-1.3567 0.1226 -0.9356 -0.3671
-1.1823 0.4105 -0.3041 -1.1571
0.1696 0.3625 -0.5146 -0.7980
0.9328 1.1301 -0.2339 -0.2234
1.2162 0.9862 -0.4444 -0.5825
0.0824 -1.8924 0.8186 0.6384
0.9328 -0.4051 2.1518 2.3620
0.6493 -1.4606 0.7484 0.5666
After normalization, each value in a column will typically be between about -3.0 and +3.0. Normalized values that are less than -6.0 or greater than +6.0 are extreme and should be investigated. The idea behind normalization is to prevent columns with large values (such as the penguin body mass) from overwhelming columns with small values (such as the bill length).
Understanding Singular Value Decomposition
If you have a matrix A with dim = n, it is possible to compute n eigenvalues (ordinary numbers like 1.234) and n associated eigenvectors, each with n values. You can think of eigenvalues and their associated eigenvectors as a decomposition of a matrix. Eigenvalues and eigenvectors are needed for PCA. But computing eigenvalues and eigenvectors directly is extremely difficult. However, it's possible to compute eigenvalues and eigenvectors indirectly using singular value decomposition (SVD).
If you have a matrix A and apply singular value decomposition, the three results are a matrix U, a vector s ("singular"), and a matrix Vh, such that A = U * S * Vh. The S term is a matrix that has the values of the s vector on the diagonal, 0s off the diagonal. The eigenvectors of A are stored in U. The eigenvalues of A can be easily computed from the values in the s vector, using the relationship eval[i] = s[i]^2 / (N-1) where N is the number of data items in matrix A. The Vh result of SVD is not used when computing eigenvalues and eigenvectors.
There are dozens of algorithms to compute SVD. The demo program uses a technique called asymmetric Jacobi rotations. It works with both square and non-square matrices.
Computing the Eigenvalues and Eigenvectors
The eigenvalues and eigenvectors of the normalized data are computed by first applying SVD:
Console.WriteLine("Computing eigenvalues and " +
"eigenvectors using SVD: ");
double[][] U;
double[][] Vh;
double[] s;
int n = stdX.Length;
int dim = stdX[0].Length;
SVD_Jacobi(MatTranspose(stdX), out U, out Vh, out s);
The source matrix X and the derived normalized stdX matrix have shape 9-by-4. Notice that the SVD_Jacobi() function is applied to the transpose of stdX, which has shape 4-by-9. Most SVD implementations assume the data is arranged so that the number of rows is less than the number of columns.
Dealing with the shapes of the matrices in PCA is not conceptually difficult, but in practice it can be very tricky. By far, most of the mistakes I make when working with PCA are related to the matrix shape issue.
Because the demo data has dim = 4, there are four eigenvalues. They are computed from the s vector result of SVD by this code:
double[] eigenVals = new double[dim];
for (int i = 0; i < dim; ++i)
eigenVals[i] = (s[i] * s[i]) / (n - 1);
The four s values are (4.9, 2.8, 1.7, 0.8). Therefore, the first eigenvalue is (4.9 * 4.9) / (9-1) = 3.0020. The second eigenvalue is (2.8 * 2.8) / (9-1) = 1.0158. And so on. All four eigenvalues are: (3.0020, 1.0158, 0.3904, 0.0918).
There are four eigenvectors stored in the U matrix result of SVD. The eigenvectors are pulled from the U matrix using these statements:
double [][] eigenVecs = MatExtract(U, dim, dim);
Console.WriteLine("Eigenvectors (not sorted, as cols): ");
MatShow(eigenVecs, 4, 9, false);
The MatExtract() helper function pulls the first four rows and four columns of U. The demo implementation of SVD returns a dim-by-dim = 4-by-4 matrix and so either of these two statements could have been used instead of calling the MatExtract() function:
double [][] eigenVecs = MatCopy(U); // copy by value
double [][] eigenVecs = U; // copy by ref
For the demo data, the four eigenvectors (as columns) are:
-0.3836 -0.7613 -0.4824 -0.2015
0.4298 -0.6466 0.6046 0.1775
-0.5932 -0.0180 0.1717 0.7863
-0.5623 0.0440 0.6101 -0.5564
The program-defined SVD_Jacobi() and MatExtract() functions return the eigenvectors as columns, so the first eigenvector is (-0.3836, 0.4298, -0.5932, -0.5623). The associated eigenvector is 3.0020. For PCA it doesn't help to overthink the deep mathematics of eigenvalues and eigenvectors. You can think of eigenvalues and eigenvectors as a kind of factorization of a matrix that captures all the information in the matrix in a sequential way.
Eigenvectors from a matrix are not unique in the sense that the sign is arbitrary. For example, an eigenvector (0.20, -0.50, 0.30) is equivalent to (-0.20, 0.50, -0.30). The eigenvector sign issue does not affect PCA.
To recap, to compute PCA, you need eigenvalues and eigenvectors. To compute eigenvalues and eigenvectors, you can use the U and s results from SVD. Whew!
Sorting the Eigenvalues and Eigenvectors
The next step in PCA is to sort the eigenvalues and their associated eigenvectors from largest to smallest. Most library SVD() functions return eigenvalues and eigenvectors already sorted, but some SVD() functions do not. The demo program assumes that the eigenvalues and eigenvectors are not necessarily sorted, just in case the SVD() implementation is changed.
First, the four eigenvalues are sorted in a way that saves the ordering so that the paired eigenvectors can be sorted in the same order:
int[] idxs = ArgSort(eigenVals); // to sort evecs
Array.Reverse(idxs); // used later
Array.Sort(eigenVals);
Array.Reverse(eigenVals);
Console.WriteLine("Eigenvalues (sorted): ");
VecShow(eigenVals, 4, 9);
For the demo data, the sorted eigenvalues are (3.0020, 1.0158, 0.3904, 0.0918). The program-defined ArgSort() function doesn't sort but returns the order in which to sort from smallest to largest. The eigenvalues are sorted from smallest to largest using the built-in Array.Sort() function and then reversed to largest to smallest using the built-in Array.Reverse() function.
The eigenvectors are sorted using these statements:
eigenVecs = MatExtractCols(eigenVecs, idxs); // sort
eigenVecs = MatTranspose(eigenVecs); // as rows
Console.WriteLine("Eigenvectors (sorted as rows):");
MatShow(eigenVecs, 4, 9, false);
The MatExtractCols() function pulls out each column in the eigenvectors, ordered by the idxs array, which holds the order in which to sort from largest to smallest. The now-sorted eigenvectors are converted from columns to rows using the MatTranspose() function only because that makes them a bit easier to read. The eigenvectors will have to be converted back to columns later. The point is that when you're looking at PCA documentation or working with PCA code, it's important to keep track of whether the eigenvectors are stored as columns (usually) or rows (sometimes).
Computing the Variance Explained
The variance explained by each of the four eigenvalue-eigenvector pairs is computed from the sorted eigenvalues:
Console.WriteLine("Computing variance explained: ");
double[] varExplained = VarExplained(eigenVals);
VecShow(varExplained, 4, 9);
For the demo data, the sum of the sorted eigenvalues is 3.0020 + 1.0158 + 0.3904 + 0.0918= 4.5000. The variance explained values are:
3.0020 / 4.5000 = 0.6671
1.0158 / 4.5000 = 0.2257
0.3904 / 4.5000 = 0.0868
0.0918 / 4.5000 = 0.0204
------
1.0000
Loosely speaking, this means that the first eigenvector captures 66.71 percent of the information in the source data. The first two eigenvectors capture 0.6671 + 0.2257 = 89.28 percent of the information. The first three eigenvectors capture 0.6671 + 0.2257 + 0.0868 = 97.96 percent of the information. All four eigenvectors capture 100 percent of the information.
Computing the Transformed Data
After computing and sorting the eigenvalues and eigenvectors from the normalized data via SVD, the next step in PCA is to use the sorted eigenvectors to compute the transformed data:
Console.WriteLine("Computing transformed data (all components): ");
double[][] transformed = MatProduct(stdX, MatTranspose(eigenVecs));
Console.WriteLine("Transformed data: ");
MatShow(transformed, 4, 9, true);
The transformed data is the matrix product of the normalized data and the eigenvectors. Because the eigenvectors were converted to rows for easier viewing, they must be passed as columns using the MatTranspose() function.
The transformed data is:
[0] 1.8846 0.6205 0.6592 -0.3440
[1] 1.3345 0.9543 0.3440 -0.2363
[2] 1.4610 0.5893 0.0603 0.7158
[3] 0.8447 -0.3894 -0.4378 0.0696
[4] 0.3924 -1.4465 0.0569 -0.0469
[5] 0.5486 -1.5813 -0.4221 -0.0953
[6] -1.6896 1.1743 -0.6539 -0.0640
[7] -3.1366 -0.3829 1.1156 0.1179
[8] -1.6394 0.4616 -0.7222 -0.1168
The demo program concludes by reconstructing the original source data from the transformed data. First the normalized data is reconstructed like so:
Console.WriteLine("Reconstructing original data: ");
double[][] reconstructed = MatProduct(transformed, eigenVecs);
Notice that reconstruction uses eigenvectors as rows rather than columns. Once again, the eigenvectors columns-vs-rows issue can be tricky when working with PCA. Next, the original source data is recovered by multiplying by the standard deviations that were used to normalize the data, and then adding the means that were used:
for (int i = 0; i < reconstructed.Length; ++i)
for (int j = 0; j < reconstructed[0].Length; ++j)
reconstructed[i][j] = (reconstructed[i][j] * stds[j]) + means[j];
MatShow(reconstructed, 4, 9, 3);
Reconstructing the original source data from the transformed data is a good way to check that nothing has gone wrong with the PCA.
Wrapping Up
Principal component analysis can be used in several ways. One of the most common is to create a graph of data that has more than two columns. For the Penguin data with four columns, there's no easy way to create a graph. But by applying PCA and then using the first of two transformed columns as the x-value and the second column as the y-value, a graph reveals that species Gentoo items are quite different from the somewhat similar Adelie and Chinstrap items.
Another way to use PCA is for anomaly detection. The idea is to use the first n columns of the transformed data, where the n columns capture roughly 60 to 80 percent of the variability, to approximately reconstruct the original source data. Data items that don't reconstruct accurately are anomalous in some way and should be investigated.