In-Depth
Priority Queues with C#
A priority queue assigns a priority to each element. Knowing how to build them is important in solving many coding problems.
A priority queue is a data structure that holds information that has some sort of priority value. When an item is removed from a priority queue, it's always the item with the highest priority. Priority queues are used in many important computer algorithms, in particular graph-based shortest-path algorithms.
Somewhat surprisingly, the Microsoft .NET Framework doesn't contain a priority queue class. One of the main reasons for this omission is that in most programming scenarios that require a priority queue, you must heavily customize features of the queue to meet your particular needs. Although there are a handful of C# priority queue implementations available on the Web, many of them are either copyrighted, inflexible or contain subtle bugs.
In this article I'll present a C# implementation of a priority queue. I'll explain the code in detail so you'll be able to modify the code presented here as necessary. In addition to being a practical addition to your personal skill set, several of the techniques used to create a priority queue can be used in other coding scenarios. I'll also present a highly effective technique to test custom priority-queue implementations.
To get a feel for exactly what a priority queue is and where I'm headed in this article, take a look at the demo run in the screenshot in Figure 1. The items in the priority queue represent employee objects that have a last name, such as "Baker," and a priority value between 1.0 and 10.0.
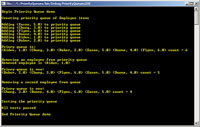
[Click on image for larger view.] |
| Figure 1. The result of the priority queue demo. |
When working with priority queues, you must be careful to be consistent with the interpretation of the meaning of the priority values. In this example, and in the majority of algorithms that use priority queues, numerically smaller values of the priority variable represent conceptually higher priorities (which at first might seem backward). So, in this example, an employee with a priority value of 1.0 has a higher priority than an employee with a priority value of 2.0.
After the demo program creates six dummy employees, they're added into the priority queue, and the queue is displayed. Notice that the employee with the highest priority (Aiden, 1.0) ends up in the front of the queue. Also notice that the queue isn't fully sorted, but appears to be semi-ordered in some way.
Behind the scenes, the priority queue is using a structure called a binary heap, which is a semi-ordered structure, as I'll explain shortly. Next, the demo program removes the front employee from the queue. After that removal, the queue is displayed and now the employee with the new highest priority (Baker, 2.0) is at the front of the queue. Then, after Baker is removed, the resulting queue has (Chung, 3.0) at the front.
The demo program concludes by running a set of automated tests. I'll explain exactly what those tests are, and why they're important when creating a custom priority queue or other custom data structure.
This article assumes you have intermediate C# programming skills. I'll present all of the code that generated the screenshot in Figure 1.
Items with a Priority
The overall structure of the demo program shown in Figure 1 is presented in Listing 1. For clarity, I embedded the PriorityQueue class definition in a demo Console Application program. In many situations you'll want to place your priority queue code in a separate class library, to create a DLL that can be used by the code that needs the queue. I also embedded the Employee class definition directly in the demo program.
When working with a priority queue, you'll almost always have a class that has some sort of priority; the Employee class in this example. Notice that class Employee inherits from the IComparable interface, which means it must implement a CompareTo method. This will be true in general, because items in a priority queue must be compared against each other during add and remove operations to reorder the queue.
The PriorityQueue class is generic, so it can be used with any item of type T that has some kind of priority field. This means that the definition has a dependency on the System.Collectons.Generic namespace, as shown at the top of Listing 1. In some situations, you might want to define a priority queue that works on a single, specific type. But because the code logic in a priority queue implementation doesn't depend on the items in the queue, in most cases a generic design is a reasonable approach.
The Employee class definition is shown in Listing 2. For simplicity, I defined the lastName and priority fields with public scope; in most cases your fields will be private, but this doesn't affect the priority queue. Here I named the field that defines an employee's priority as priority. In many situations, an object's priority is implied. For example, in a graph-based shortest-path algorithm, items have a distance field that acts as the priority. Priority fields are almost always either type int or type double.
The required CompareTo method can be coded in several ways, but I prefer the approach in Listing 2. As mentioned earlier, in this example (and in most cases) lower-priority numeric values mean higher priority. In the rare cases where the opposite is true, there are two main ways to handle the situation. First, you can modify the CompareTo method to operate in reverse by changing the two inequality operators. This is the method I recommend. Second, you can modify the code logic in the priority queue add and remove operations. This approach tends to be more error-prone, so I advise against it in most situations.
In some situations, the items you're dealing with might not have a single field that determines the item's priority. For example, an employee's priority might depend on two fields such as years of service and job category. In these situations you must code the CompareTo method to take all relevant fields into account.
Understanding Binary Heaps
A simplistic way to implement a priority queue would be to use an array or a List collection for storage. After each addition operation (at the end of the list), the list could be sorted so that the highest priority (lowest value) is at the front (index [0]) of the list. Likewise, after a removal (of the front item), the list could be re-sorted so that the item with the new highest priority is at the front of the list. However, most algorithms that require a priority queue have lots of data and perform many additions, removals or both. Constantly sorting a list can lead to unacceptable performance.
An alternative to using a List collection for priority queue storage is to use a binary heap. A binary heap is a form of conceptual storage (meaning many different implementations are possible), as shown in Figure 2.
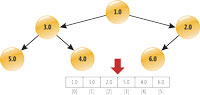
[Click on image for larger view.] |
| Figure 2. Binary heap storage. |
Binary heaps can significantly improve the performance of large priority queues. A min binary heap is ordered storage that has the lowest priority value in the root node. The heap is populated top-to-bottom and left-to-right, so each node that isn't in the bottom row has two child nodes, except for possibly one node, which will have only a left child.
Each child node has a priority value greater than or equal to the priority value of the parent node. There are two things going on here: the fact that the highest priority node is at the root of a binary heap means it can always be found immediately. Second, the heap ordering of the rest of the nodes enables quick updates after a new node is added or the root node is removed.
A binary heap can be implemented using pointers or references. But a binary heap can also be efficiently implemented using a List collection, as shown in Figure 2. The trick is that for any parent node in the list at index [pi], the two child nodes are located at indexes [2 * pi + 1] and [2 * pi + 2].
For example, in Figure 2 the node with priority 3.0 is at index [1]. Its left child is at index [2 * 1 + 1] = [3] and its right child is at index [2 * 1 + 2] = [4]. Very clever! For a given child node at index [ci], its parent is located at index [(ci - 1) / 2].
Adding an Item to a Priority Queue
The PriorityQueue class definition begins as:
public class PriorityQueue <T> where T : IComparable <T>
{
private List <T> data;
public PriorityQueue()
{
this.data = new List <T>();
}
The first line of the class can be loosely interpreted as, "This is the definition of a PriorityQueue that works with items of type T (to be specified later), where that type T is required to have a CompareTo method defined." The items are stored in a generic List named data. The PriorityQueue constructor instantiates the List collection.
The method to add an item to a priority queue is surprisingly short (see Listing 3).
The method is named Enqueue. Because the term enqueue is often associated with a pure first-in, first-out ordinary queue data structure, some developers prefer to name this method Add.
If you scan through the code you'll see that none of the logic depends on what the data items are; the logic only requires a CompareTo method consistent with your definition of priority. In spite of its shortness, method Enqueue is quite tricky. The item to add is added at the end of the data List. The while loop starts by placing child index ci at the end of the list, then checking the priority value at the parent index pi. If the child and parent are in order with regard to a binary heap (child priority value is greater than or equal to the parent priority), then the method is done. Otherwise, the child node bubbles up until it's in the correct position. Because the value of index ci is halved in each iteration, the maximum number of operations is O(lg n), which is much better than the O(n lg n) for a simple implementation that doesn't use a binary heap.
Removing an Item
The method to remove an item from a priority queue is shown in Listing 4. The method assumes that the priority queue isn't empty. You might want to modify the code to throw an exception if the queue is empty. The variable li is the last index. The front item is removed by making a copy of it, then overwriting the item at location [0] with the item in the last location. Index ci is initially set to the left child of the parent at index [0].
The Dequeue logic has to compare the priority value of the smaller of the two children, which accounts for the first call to CompareTo. If the parent and the child are out of order, the child node trickles down the binary heap until the parent and child nodes are in order. Because the value of index ci doubles each time through the loop in Dequeue, removing an item is O(lg n).
Miscellaneous Priority Queue Methods
Calling the priority queue is straightforward. The code in the demo program that adds Employee items to the priority queue is:
Employee e1 = new Employee("Aiden", 1.0);
Employee e2 = new Employee("Baker", 2.0);
// And so on for e3, e4, e5, e6
Console.WriteLine("Adding " + e5.ToString() + " to priority queue");
pq.Enqueue(e5);
Console.WriteLine("Adding " + e3.ToString() + " to priority queue");
pq.Enqueue(e3);
// And so on for e6, e4, e1, e2
Depending on the requirements of the algorithm that uses a priority queue, you'll likely want to add some methods to supplement Enqueue and Dequeue. To display the priority queue, you can write a simple ToString method along the lines of:
public override string ToString()
{
string s = "";
for (int i = 0; i < data.Count; ++i)
s += data[i].ToString() + " ";
s += "count = " + data.Count;
return s;
}
The ToString method can be called like so:
Console.WriteLine("Priory queue is: ");
Console.WriteLine(pq.ToString());
To check if a priority queue is empty or not, you'll likely want to code a Count method or an IsEmpty method. For example:
public int Count()
{
return data.Count;
}
Another common utility function is a Peek method that returns the front item in the priority queue without removing the item:
public T Peek()
{
T frontItem = data[0];
return frontItem;
}
Calling these methods could look like:
PriorityQueue <Employee > pq = new PriortyQueue <Employee >();
// Enqueue some Employee items
if (pq.Count() > 0)
{
Employee e = pq.Peek();
Console.WriteLine("The front employee is " + e.ToString());
}
Testing a Custom Data Structure
When creating a custom data structure like the priority queue described in this article, research suggests that a good way to test the custom data structure is to define a method that verifies the state of the data structure, then use a random input and output approach.
The idea is best explained by a concrete example. After any item is added or removed from the priority queue, some pretty tricky code is invoked. But after every operation, the binary heap property (the parent priority value must be less than or equal to the priority value of the child nodes) of the data List collection should still hold.
Consider the method in Listing 5 to check a priority queue's state invariant.
The IsConsistent method walks through each node stored in the data List collection. The index of the left child (lci) and the right child (rci) are computed. Then the priority values of the children (if they exist) are compared with the priority value of the parent and checked to make sure the parent priority value is less than the children's priority values.
An alternative approach would be to iterate through the data List, interpreting each node as a child node, and computing and checking the priority value of the parent node.
With a state consistency method in hand, a simple but highly effective test method can be written as shown in Listing 6.
The test method instantiates a Random object and a priority queue. The method loops a specified number of times (typically some large number like 1,000,000 or more). At each iteration, a random decision to enqueue or dequeue is made by generating an integer between 0 and 1 inclusive.
If the decision is made to add an item, a random Employee item is generated that has a last name such as "123man" and a random priority value between 1.0 and 100.0, and the random Employee is added to the queue.
If the decision is to remove an item, the test method checks to see if that's possible (count > 0) and then does so. After every enqueue or dequeue operation, the state of the underlying data List is checked to verify the binary heap property still holds. Calling the test method could look like:
TestPriorityQueue(1000000);
Research has shown that this approach to testing a custom data structure is extremely effective at uncovering difficult-to-detect bugs.