Neural Network Lab
Neural Network How-To: Code an Evolutionary Optimization Solution
Evolutionary optimization can be used to train a neural network. A virtual chromosome holds the neural network's weights and bias values, and the error term is the average of all errors between the network's computed outputs and the training data target outputs. Learn how to code the solution.
Neural networks are software systems that can be used to make predictions. For example, predicting whether the price of some company's stock will go up, go down, or stay the same based on inputs such as bank interest rates, number of mentions on social media, and so on. A neural network is essentially a complex mathematical function.
Training a neural network is the process of finding a set of numeric weight values so that, for a given set of training data with known input and output values, the network's computed output values closely match the known output values. After these best weight values have been found, they can be placed into the neural network and used to predict the output of new input data that has unknown outputs.
By far the most common technique for training a neural network is called the back-propagation algorithm. Two major alternative techniques are particle swarm optimization (PSO) and evolutionary optimization (EO). This article presents a complete demo of neural network training using EO.
Take a look at the demo program in Figure 1. The demo uses EO to train a neural network that predicts the species of an Iris flower ("setosa," "versicolor," "virginica") based on the flower's sepal (green covering) length, sepal width, petal length and petal width. There are 24 training items. After training completed, the best set of weights found were placed into the neural network. The network correctly predicted the species of 5/6 = 0.8333 of six test data items.
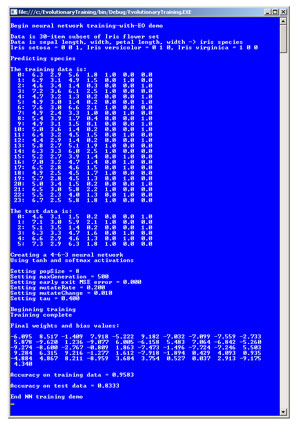 [Click on image for larger view.]
Figure 1. Neural Network Training Demo
[Click on image for larger view.]
Figure 1. Neural Network Training Demo
This article assumes you have a solid grasp of neural network concepts, including the feed-forward mechanism, activation functions, and weights and biases, and that you have advanced programming skills. The demo is coded using C# but you should be able to refactor the code to other languages such as JavaScript or Visual Basic .NET without too much difficulty. Most normal error checking has been omitted to keep the size of the code small and the main ideas as clear as possible.
Evolutionary Optimization
Evolutionary optimization is a type of genetic algorithm. The process is illustrated in Figure 2. The population matrix is a set of potential solutions, that is, a set of neural network weights. In the figure, there are six individuals, or chromosomes, in the population. Each chromosome has six genes that represent six neural network weights. The population here is artificially small -- a realistic neural network would normally have 50 or more weights and 20 or more individuals.
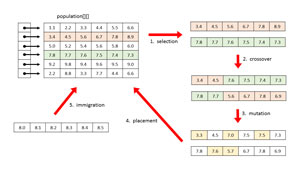 [Click on image for larger view.]
Figure 2. Evolutionary Optimization Algorithm
[Click on image for larger view.]
Figure 2. Evolutionary Optimization Algorithm
Step one is to select two good, but not necessarily best, parent individuals from the population. In step two, crossover is used to generate two child individuals, which hopefully combine good characteristics of the parents to give even better solutions. In step three, the two children are randomly mutated slightly to introduce new information into the system. In step four, the children are placed into the population, replacing two weak individuals. Steps one through four are collectively called reproduction and are core evolutionary optimization mechanisms. Step five, immigration, is optional. A random individual is generated and placed into the population, replacing a weak individual. Evolutionary optimization repeats steps one through five until some stopping condition, typically a maximum number of generations, is reached.
Overall Program Structure
The overall program structure of the demo, with most WriteLine statements removed and some minor edits to save space, is presented in Listing 1. To create the demo, I launched Visual Studio and created a new C# console application project named EvolutionaryTraining. The demo has no .NET version dependencies, so any version of Visual Studio should work. After the template code loaded, in the Solution Explorer window I renamed file Program.cs to the more descriptive EvolutionaryTrainingProgram.cs, and Visual Studio automatically renamed class Program for me.
Listing 1: Overall Program Structure
using System;
namespace EvolutionaryTraining
{
class EvolutionaryTrainingProgram
{
static void Main(string[] args)
{
double[][] trainData = new double[24][];
trainData[0] = new double[] { 6.3, 2.9, 5.6, 1.8, 1, 0, 0 };
trainData[1] = new double[] { 6.9, 3.1, 4.9, 1.5, 0, 1, 0 };
trainData[2] = new double[] { 4.6, 3.4, 1.4, 0.3, 0, 0, 1 };
trainData[3] = new double[] { 7.2, 3.6, 6.1, 2.5, 1, 0, 0 };
trainData[4] = new double[] { 4.7, 3.2, 1.3, 0.2, 0, 0, 1 };
trainData[5] = new double[] { 4.9, 3, 1.4, 0.2, 0, 0, 1 };
trainData[6] = new double[] { 7.6, 3, 6.6, 2.1, 1, 0, 0 };
trainData[7] = new double[] { 4.9, 2.4, 3.3, 1, 0, 1, 0 };
trainData[8] = new double[] { 5.4, 3.9, 1.7, 0.4, 0, 0, 1 };
trainData[9] = new double[] { 4.9, 3.1, 1.5, 0.1, 0, 0, 1 };
trainData[10] = new double[] { 5, 3.6, 1.4, 0.2, 0, 0, 1 };
trainData[11] = new double[] { 6.4, 3.2, 4.5, 1.5, 0, 1, 0 };
trainData[12] = new double[] { 4.4, 2.9, 1.4, 0.2, 0, 0, 1 };
trainData[13] = new double[] { 5.8, 2.7, 5.1, 1.9, 1, 0, 0 };
trainData[14] = new double[] { 6.3, 3.3, 6, 2.5, 1, 0, 0 };
trainData[15] = new double[] { 5.2, 2.7, 3.9, 1.4, 0, 1, 0 };
trainData[16] = new double[] { 7, 3.2, 4.7, 1.4, 0, 1, 0 };
trainData[17] = new double[] { 6.5, 2.8, 4.6, 1.5, 0, 1, 0 };
trainData[18] = new double[] { 4.9, 2.5, 4.5, 1.7, 1, 0, 0 };
trainData[19] = new double[] { 5.7, 2.8, 4.5, 1.3, 0, 1, 0 };
trainData[20] = new double[] { 5, 3.4, 1.5, 0.2, 0, 0, 1 };
trainData[21] = new double[] { 6.5, 3, 5.8, 2.2, 1, 0, 0 };
trainData[22] = new double[] { 5.5, 2.3, 4, 1.3, 0, 1, 0 };
trainData[23] = new double[] { 6.7, 2.5, 5.8, 1.8, 1, 0, 0 };
double[][] testData = new double[6][];
testData[0] = new double[] { 4.6, 3.1, 1.5, 0.2, 0, 0, 1 };
testData[1] = new double[] { 7.1, 3, 5.9, 2.1, 1, 0, 0 };
testData[2] = new double[] { 5.1, 3.5, 1.4, 0.2, 0, 0, 1 };
testData[3] = new double[] { 6.3, 3.3, 4.7, 1.6, 0, 1, 0 };
testData[4] = new double[] { 6.6, 2.9, 4.6, 1.3, 0, 1, 0 };
testData[5] = new double[] { 7.3, 2.9, 6.3, 1.8, 1, 0, 0 };
ShowMatrix(trainData, trainData.Length, 1, true);
ShowMatrix(testData, testData.Length, 1, true);
const int numInput = 4;
const int numHidden = 6;
const int numOutput = 3;
NeuralNetwork nn =
new NeuralNetwork(numInput, numHidden, numOutput);
// Training parameters specific to EO
int popSize = 8;
int maxGeneration = 500;
double exitError = 0.0;
double mutateRate = 0.20;
double mutateChange = 0.01;
double tau = 0.40;
double[] bestWeights = nn.Train(trainData, popSize, maxGeneration,
exitError, mutateRate, mutateChange, tau);
ShowVector(bestWeights, 10, 3, true);
nn.SetWeights(bestWeights);
double trainAcc = nn.Accuracy(trainData);
Console.Write("\nAccuracy on training data = ");
Console.WriteLine(trainAcc.ToString("F4"));
double testAcc = nn.Accuracy(testData);
Console.Write("\nAccuracy on test data = ");
Console.WriteLine(testAcc.ToString("F4"));
Console.WriteLine("\nEnd NN training demo");
Console.ReadLine();
} // Main
static void ShowVector(double[] vector, int valsPerRow,
int decimals, bool newLine)
{
for (int i = 0; i < vector.Length; ++i)
{
if (i % valsPerRow == 0) Console.WriteLine("");
if (vector[i] >= 0.0) Console.Write(" ");
Console.Write(vector[i].ToString("F" + decimals) + " ");
}
if (newLine == true)
Console.WriteLine("");
}
static void ShowMatrix(double[][] matrix, int numRows,
int decimals, bool newLine)
{
for (int i = 0; i < numRows; ++i)
{
Console.Write(i.ToString().PadLeft(3) + ": ");
for (int j = 0; j < matrix[i].Length; ++j)
{
if (matrix[i][j] >= 0.0)
Console.Write(" ");
else
Console.Write("-"); ;
Console.Write(Math.Abs(matrix[i][j]).ToString("F" +
decimals) + " ");
}
Console.WriteLine("");
}
if (newLine == true)
Console.WriteLine("");
}
} // Program
public class NeuralNetwork
{
// Defined here
}
public class Individual : IComparable<Individual>
{
// Defined here
}
} // ns
At the top of the source code I deleted all namespace references except the reference to System. If you scan Listing 1 you'll see the program class has a single Main method and two helpers, ShowVector and ShowMatrix. There are two program-defined classes: Class NeuralNetwork encapsulates most of the code logic, in particular the Train method, and is fairly complex, while Class Individual is a simple container class, which defines a single possible set of weights and bias values for the neural network.
The demo begins by setting up the 24 training items and six test items:
double[][] trainData = new double[24][];
trainData[0] = new double[] { 6.3, 2.9, 5.6, 1.8, 1, 0, 0 };
... etc.
These are a subset of the well-known 150-item Fisher's data set. In most cases, you would read training and test data from a text file or SQL database. After setting up the data, the demo instantiates a 4-6-3 fully connected feed-forward neural network because there are four inputs and three possible output classes. The choice of six for the number of hidden nodes is arbitrary.
Next, the demo assigns values for the EO training parameters:
int popSize = 8;
int maxGeneration = 500;
double exitError = 0.0;
double mutateRate = 0.20;
double mutateChange = 0.01;
double tau = 0.40;
Each type of neural network training algorithm has a different set of parameters. Back-propagation uses a learning rate, momentum and so on. PSO uses number of particles, cognitive and social weights, and so on. Here, the EO population size is the number of individuals. More individuals generally leads to a better solution, at the expense of performance. The maximum generation variable is the maximum number of iterations the EO select-crossover-mutate process will execute.
Variable exitError sets a short-circuit exit threshold if the best set of weights found produces an error less the threshold. Here, exitError is set to zero so an early exit will not occur. Variable mutateRate controls how many genes in a newly-generated child's chromosome will be mutated. Variable mutateChange controls the magnitude of the change of mutated genes. Variable tau is the "selection pressure" and controls the likelihood that the two best individuals in the population will be selected as parents for reproduction. Larger values of tau increase the chances that the two best individuals will be chosen.
Choosing the best values for the EO parameters is more art than science, and typically boils down to trial and error. This factor is generally considered the primary weakness of EO and genetic algorithms.
The demo trains and evaluates the neural network with these key lines of code:
double[] bestWeights = nn.Train(trainData, popSize, maxGeneration,
exitError, mutateRate, mutateChange, tau);
nn.SetWeights(bestWeights);
double trainAcc = nn.Accuracy(trainData);
double testAcc = nn.Accuracy(testData);
The Individual Class
The definition of the Individual class is given in Listing 2. The class inherits from the IComparable interface so that a collection of Individual objects can be sorted automatically from smallest error to largest. The class contains a Random object for use in the class constructor to generate a chromosome with random gene values, each of which is between minGene and maxGene.
Notice the error value isn't passed in as a parameter to the constructor. This is a bit subtle. The error for an Individual object depends on the object's chromosome, which represents a neural network's weights and bias values, and the training data, which in most cases isn't part of the neural network. Therefore, an Individual object is first instantiated with a random chromosome by a call to the constructor, then the error is computed using the training data, and then the error value is assigned to the object.
Listing 2: Individual Class
public class Individual : IComparable<Individual>
{
public double[] chromosome; // Potential solution
public double error; // Smaller better
private int numGenes; // (numWeights)
private double minGene; // Smallest value for a chromosome
private double maxGene;
private double mutateRate;
private double mutateChange;
static Random rnd = new Random(0);
public Individual(int numGenes, double minGene, double maxGene,
double mutateRate, double mutateChange)
{
this.numGenes = numGenes;
this.minGene = minGene;
this.maxGene = maxGene;
this.mutateRate = mutateRate;
this.mutateChange = mutateChange;
this.chromosome = new double[numGenes];
for (int i = 0; i < this.chromosome.Length; ++i)
this.chromosome[i] = (maxGene - minGene) *
rnd.NextDouble() + minGene;
// this.error supplied after calling ctor!
}
public int CompareTo(Individual other)
{
if (this.error < other.error) return -1;
else if (this.error > other.error) return 1;
else return 0;
}
}
The Neural Network Class
Using EO to train a neural network is more complex than using PSO or backpropagation. The overall structure of the NeuralNetwork class is presented in Listing 3.
Listing 3: NeuralNetwork Class Structure
public class NeuralNetwork
{
private int numInput;
private int numHidden;
private int numOutput;
private double[] inputs;
private double[][] ihWeights;
private double[] hBiases;
private double[] hOutputs;
private double[][] hoWeights;
private double[] oBiases;
private double[] outputs;
private Random rnd;
public NeuralNetwork(int numInput, int numHidden,
int numOutput) { . . }
private static double[][] MakeMatrix(int rows, int cols) { . . }
public void SetWeights(double[] weights) { . . }
public double[] GetWeights() { . . }
public double[] ComputeOutputs(double[] xValues) { . . }
private static double HyperTanFunction(double x) { . . }
private static double[] Softmax(double[] oSums) { . . }
public double[] Train(double[][] trainData,
int popSize, int maxGeneration, double exitError,
double mutateRate, double mutateChange, double tau) { . . }
private Individual[] Select(int n, Individual[] population,
double tau) { . . }
private Individual[] Reproduce(Individual parent1,
Individual parent2, double minGene, double maxGene,
double mutateRate, double mutateChange) { . . }
private void Mutate(Individual child, double maxGene,
double mutateRate, double mutateChange) { . . }
private static void Place(Individual child1, Individual child2,
Individual[] population) { . . }
private double MeanSquaredError(double[][] trainData,
double[] weights) { . . }
public double Accuracy(double[][] testData) { . . }
return (numCorrect * 1.0) / (numCorrect + numWrong);
private static int MaxIndex(double[] vector) { . . }
}
Notice field rnd in the class definition. Most forms of neural network training have a random element of some sort. For back-propagation, the training items are often presented in random order. PSO has several random operations. Training using EO uses randomness in selection, crossover, mutation and immigration.
Private method MakeMatrix is a helper for the NeuralNetwork constructor. Methods SetWeights, GetWeights and ComputeOutputs are generic to all neural network implementations. Private methods HyperTanFunction and Softmax implement hidden node layer hyperbolic tangent activation and output node layer softmax activation, and are called by method ComputeOutputs.
Method Train implements EO and accepts the parameters described earlier. Method Train calls helpers Select (selection), Reproduce (crossover and mutation) and Place (placement), as described in Figure 2. Helper Reproduce calls a sub-helper Mutate.
Private method MeanSquaredError measures how far away computed output values are from the desired training output values. Public method Accuracy computes the percentage of correct classifications and uses helper method MaxIndex.
The Train Method
Method Train is presented in Listing 4. The values for variables minGene and maxGene are hardcoded as -10.0 and +10.0, respectively. These values work for the raw Iris data set because the input values are all relatively similar in magnitude. In most situations, however, the training and test data should be normalized to ensure the data magnitudes are similar.
Listing 4: Method Train Definition
public double[] Train(double[][] trainData,
int popSize, int maxGeneration, double exitError,
double mutateRate, double mutateChange, double tau)
{
// Use Evolutionary Optimization to train NN
int numWeights = (this.numInput * this.numHidden) +
(this.numHidden * this.numOutput) + this.numHidden +
this.numOutput;
double minX = -10.0; // (minGene) could be parameters.
double maxX = 10.0;
// Initialize population
Individual[] population = new Individual[popSize];
double[] bestSolution = new double[numWeights];
double bestError = double.MaxValue; // smaller better
for (int i = 0; i < population.Length; ++i)
{
population[i] = new Individual(numWeights, minX, maxX,
mutateRate, mutateChange); // random values
double error = MeanSquaredError(trainData,
population[i].chromosome);
population[i].error = error;
if (population[i].error < bestError)
{
bestError = population[i].error;
Array.Copy(population[i].chromosome, bestSolution, numWeights);
}
}
// Main EO processing loop
int gen = 0; bool done = false;
while (gen < maxGeneration && done == false)
{
Individual[] parents = Select(2, population, tau);
Individual[] children = Reproduce(parents[0], parents[1],
minX, maxX, mutateRate, mutateChange);
children[0].error = MeanSquaredError(trainData,
children[0].chromosome);
children[1].error = MeanSquaredError(trainData,
children[1].chromosome);
Place(children[0], children[1], population);
// Immigration
Individual immigrant = new Individual(numWeights, minX, maxX,
mutateRate, mutateChange);
immigrant.error = MeanSquaredError(trainData,
immigrant.chromosome);
population[population.Length - 3] = immigrant; // Third worst
for (int i = popSize - 3; i < popSize; ++i) // Check 3 new
{
if (population[i].error < bestError)
{
bestError = population[i].error;
population[i].chromosome.CopyTo(bestSolution, 0);
if (bestError < exitError)
{
done = true;
Console.WriteLine("\nEarly exit at generation " + gen);
}
}
}
++gen;
}
return bestSolution;
}
Helper method Select implements the tournament selection algorithm and is presented in Listing 5. The method creates a random ordering of the indices of the population and then selects tau-percent of those random individuals. The selected individuals are sorted from smallest error to largest error, and the top n of those individuals are returned. There are several alternative selection algorithms -- in particular, one named roulette wheel selection.
Listing 5: Method Select
private Individual[] Select(int n, Individual[] population,
double tau)
{
int popSize = population.Length;
int[] indexes = new int[popSize];
for (int i = 0; i < indexes.Length; ++i)
indexes[i] = i;
for (int i = 0; i < indexes.Length; ++i) // Shuffle
{
int r = rnd.Next(i, indexes.Length);
int tmp = indexes[r];
indexes[r] = indexes[i];
indexes[i] = tmp;
}
int tournSize = (int)(tau * popSize);
if (tournSize < n) tournSize = n;
Individual[] candidates = new Individual[tournSize];
for (int i = 0; i < tournSize; ++i)
candidates[i] = population[indexes[i]];
Array.Sort(candidates);
Individual[] results = new Individual[n];
for (int i = 0; i < n; ++i)
results[i] = candidates[i];
return results;
}
Helper method Reproduce (to method Train) is presented in Listing 6. The method implements what's called single-point crossover, as illustrated in Figure 2. There are several alternatives, in particular using two crossover points instead of one point. In my opinion, research results in alternative crossover approaches aren't conclusive. Notice after mutation, the children's error fields aren't set, so those values must be set by Train, the caller method.
Listing 6: Reproduce Method
private Individual[] Reproduce(Individual parent1,
Individual parent2, double minGene, double maxGene,
double mutateRate, double mutateChange)
{
int numGenes = parent1.chromosome.Length;
// Crossover point: 0 means "between 0 and 1"
int cross = rnd.Next(0, numGenes - 1);
Individual child1 = new Individual(numGenes, minGene, maxGene,
mutateRate, mutateChange);
Individual child2 = new Individual(numGenes, minGene, maxGene,
mutateRate, mutateChange);
for (int i = 0; i <= cross; ++i)
child1.chromosome[i] = parent1.chromosome[i];
for (int i = cross + 1; i < numGenes; ++i)
child2.chromosome[i] = parent1.chromosome[i];
for (int i = 0; i <= cross; ++i)
child2.chromosome[i] = parent2.chromosome[i];
for (int i = cross + 1; i < numGenes; ++i)
child1.chromosome[i] = parent2.chromosome[i];
Mutate(child1, maxGene, mutateRate, mutateChange);
Mutate(child2, maxGene, mutateRate, mutateChange);
Individual[] result = new Individual[2];
result[0] = child1;
result[1] = child2;
return result
}
Sub-helper method Mutate is quite short and simple:
private void Mutate(Individual child, double maxGene,
double mutateRate, double mutateChange)
{
double hi = mutateChange * maxGene; double lo = -hi;
for (int i = 0; i < child.chromosome.Length; ++i) {
if (rnd.NextDouble() < mutateRate) {
double delta = (hi - lo) * rnd.NextDouble() + lo;
child.chromosome[i] += delta;
}
}
}
The mutateRate parameter is essentially the probability that a particular gene will be mutated. If a gene is targeted for mutation, its value is adjusted up or down by a random amount proportional to the value of the mutateChange and maxGene parameters. For example, suppose maxGene = 10.0 and mutateChange is 0.01. The mutation delta will be a random value between -1.0 and +1.0. There are many possible alternative mutation mechanisms.
Helper method Place is also short and simple:
private static void Place(Individual child1, Individual child2,
Individual[] population)
{
int popSize = population.Length;
Array.Sort(population);
population[popSize - 1] = child1;
population[popSize - 2] = child2;
}
The population is first sorted. Recall that Individual objects inherit from the IComparable interface, so thatsorting occurs automatically from smallest error to largest. After sorting, the two worst Individual objects will be located at indices popSize-1 and popSize-2. An important alternative approach is to replace two bad, but not necessarily the worst, individuals using tournament selection. Similarly, in method Train, the immigration process deterministically places the randomly generated immigrant at the index of the third worst individual, and a probabilistic approach can be used instead.
Measuring Error and Accuracy
Method MeanSquaredError is used during training to find the best set of neural network weights (or equivalently, the best chromosome). Method Accuracy is used after training to evaluate the effectiveness of the best set of weights found. The two methods, and a helper, are presented in Listing 7.
Listing 7: Methods MeanSquaredError and Accuracy
private double MeanSquaredError(double[][] trainData,
double[] weights)
{
// How far off are computed values from desired values?
this.SetWeights(weights);
double[] xValues = new double[numInput]; // inputs
double[] tValues = new double[numOutput]; // targets
double sumSquaredError = 0.0;
for (int i = 0; i < trainData.Length; ++i)
{
// Assumes data has x-values followed by y-values
Array.Copy(trainData[i], xValues, numInput);
Array.Copy(trainData[i], numInput, tValues, 0,
numOutput);
double[] yValues = this.ComputeOutputs(xValues);
for (int j = 0; j < yValues.Length; ++j)
sumSquaredError += ((yValues[j] - tValues[j]) *
(yValues[j] - tValues[j]));
}
return sumSquaredError / trainData.Length;
}
public double Accuracy(double[][] testData)
{
// Percentage correct using winner takes all
int numCorrect = 0;
int numWrong = 0;
double[] xValues = new double[numInput]; // Inputs
double[] tValues = new double[numOutput]; // Targets
double[] yValues; // Computed outputs
for (int i = 0; i < testData.Length; ++i)
{
Array.Copy(testData[i], xValues, numInput);
Array.Copy(testData[i], numInput, tValues, 0,
numOutput);
yValues = this.ComputeOutputs(xValues);
int maxIndex = MaxIndex(yValues);
if (tValues[maxIndex] == 1.0) // Not so nice
++numCorrect;
else
++numWrong;
}
return (numCorrect * 1.0) / (numCorrect + numWrong);
}
private static int MaxIndex(double[] vector)
{
int bigIndex = 0;
double biggestVal = vector[0];
for (int i = 0; i < vector.Length; ++i)
{
if (vector[i] > biggestVal)
{
biggestVal = vector[i]; bigIndex = i;
}
}
return bigIndex;
}
For neural networks that perform classification (like the demo network), an important alternative to using mean squared error for computing error during training is to use a function called cross-entropy error.
Core Neural Network Functionality
For the sake of completeness, the NeuralNetwork class constructor, helper method MakeMatrix, and core neural network methods SetWeights, GetWeights, ComputeOutputs, HyperTanFunction and Softmax, are presented in Listing 8. These methods have been described in detail in previous articles in this series.
Listing 8: Core Neural Network Methods
public NeuralNetwork(int numInput, int numHidden, int numOutput)
{
this.numInput = numInput;
this.numHidden = numHidden;
this.numOutput = numOutput;
this.inputs = new double[numInput];
this.ihWeights = MakeMatrix(numInput, numHidden);
this.hBiases = new double[numHidden];
this.hOutputs = new double[numHidden];
this.hoWeights = MakeMatrix(numHidden, numOutput);
this.oBiases = new double[numOutput];
this.outputs = new double[numOutput];
rnd = new Random(0);
}
private static double[][] MakeMatrix(int rows, int cols)
{
// Helper for NN ctor
double[][] result = new double[rows][];
for (int r = 0; r < result.Length; ++r)
result[r] = new double[cols];
return result;
}
public void SetWeights(double[] weights)
{
// Sets weights and biases from weights[]
int numWeights = (numInput * numHidden) +
(numHidden * numOutput) + numHidden + numOutput;
if (weights.Length != numWeights)
throw new Exception("Bad weights array length: ");
int k = 0; // points into weights param
for (int i = 0; i < numInput; ++i)
for (int j = 0; j < numHidden; ++j)
ihWeights[i][j] = weights[k++];
for (int i = 0; i < numHidden; ++i)
hBiases[i] = weights[k++];
for (int i = 0; i < numHidden; ++i)
for (int j = 0; j < numOutput; ++j)
hoWeights[i][j] = weights[k++];
for (int i = 0; i < numOutput; ++i)
oBiases[i] = weights[k++];
}
public double[] GetWeights()
{
// Returns current weights and biases
int numWeights = (numInput * numHidden) +
(numHidden * numOutput) + numHidden + numOutput;
double[] result = new double[numWeights];
int k = 0;
for (int i = 0; i < ihWeights.Length; ++i)
for (int j = 0; j < ihWeights[0].Length; ++j)
result[k++] = ihWeights[i][j];
for (int i = 0; i < hBiases.Length; ++i)
result[k++] = hBiases[i];
for (int i = 0; i < hoWeights.Length; ++i)
for (int j = 0; j < hoWeights[0].Length; ++j)
result[k++] = hoWeights[i][j];
for (int i = 0; i < oBiases.Length; ++i)
result[k++] = oBiases[i];
return result;
}
public double[] ComputeOutputs(double[] xValues)
{
// Feed-forward mechanism for NN classifier
if (xValues.Length != numInput)
throw new Exception("Bad xValues array length");
double[] hSums = new double[numHidden];
double[] oSums = new double[numOutput];
for (int i = 0; i < xValues.Length; ++i)
this.inputs[i] = xValues[i];
for (int j = 0; j < numHidden; ++j)
for (int i = 0; i < numInput; ++i)
hSums[j] += this.inputs[i] * this.ihWeights[i][j];
for (int i = 0; i < numHidden; ++i)
hSums[i] += this.hBiases[i];
for (int i = 0; i < numHidden; ++i)
this.hOutputs[i] = HyperTanFunction(hSums[i]);
for (int j = 0; j < numOutput; ++j)
for (int i = 0; i < numHidden; ++i)
oSums[j] += hOutputs[i] * hoWeights[i][j];
for (int i = 0; i < numOutput; ++i)
oSums[i] += oBiases[i];
double[] softOut = Softmax(oSums);
Array.Copy(softOut, outputs, softOut.Length);
double[] retResult = new double[numOutput];
Array.Copy(this.outputs, retResult, retResult.Length);
return retResult;
}
private static double HyperTanFunction(double x)
{
if (x < -20.0) return -1.0;
else if (x > 20.0) return 1.0;
else return Math.Tanh(x);
}
private static double[] Softmax(double[] oSums)
{
double max = oSums[0];
for (int i = 0; i < oSums.Length; ++i)
if (oSums[i] > max) max = oSums[i];
// Determine scaling factor
double scale = 0.0;
for (int i = 0; i < oSums.Length; ++i)
scale += Math.Exp(oSums[i] - max);
double[] result = new double[oSums.Length];
for (int i = 0; i < oSums.Length; ++i)
result[i] = Math.Exp(oSums[i] - max) / scale;
return result; // Scaled so xi sum to 1.0
}
Pros and Cons
Back-propagation is by far the most common neural network training technique. Back-propagation is relatively simple to implement, has very few options, and is relatively fast. However back-propagation is highly sensitive to the values used for its free parameters (learning rate, momentum and so on) and can frequently give terrible results. Evolutionary optimization is more difficult to code, has many options and tends to be slower than back-propagation, but gives terrible results less often than back-propagation. Based on my experience, when working with a neural network, I generally try back-propagation training first and then check my results using either particle swarm optimization or evolutionary optimization training.