In-Depth
Solving Sliding Tiles with Artificial Intelligence (and Some C#)
True artificial intelligence is years away. But we can demonstrate the challenges of AI decisionmaking using C# to derive solutions for the classic sliding tiles puzzle.
- By Arnaldo Pérez Castaño
- 10/30/2015
[Editor's Note: Several readers have been asking about a sample file, Heap.cs, that was missing from the Code Download. It's there now; apologies for the inconvenience to the author and to our readers.]
Artificial intelligence refers to the process by which we develop a nonliving rational agent. A rational agent is an entity capable of perceiving his environment and acting rationally to the perceptions obtained on it. Rationality in this sense is given by the appropriate decision-making of the agent, considered appropriated if it's aimed towards maximizing some desired outcome.
Humans are seen as the finest example of living rational agents -- we receive perceptions from our environment all the time and react to them by making decisions that usually go in favor of our standard of living.
The human mind is still the most capable, complex and sophisticated intelligence in the known universe. There's probably not going to be an artificial intelligence in the near future that will achieve the power that the human mind currently possesses. Even if that's the case, if we have such sophisticated, complex, evolved mind, why do we need to create artificial intelligences?
For some domain-specific environments, artificial intelligences provide a better reaction to perceptions than the reaction provided by humans. Artificial intelligences present a feasible, sometimes optimal outcome to extremely complicated problems by taking advantage of their facility to compute millions of instructions in short periods of time. Even though we have a more elaborated intelligence in terms of reasoning, computers actually defeat us in the field of calculations. For calculation-related environments we create artificial intelligences that can speed up the process of obtaining a maximized outcome.
The calculator, that simple machine that we frequently use in our daily life is a mere example of how we exploit an artificial intelligence in a calculation environment; we lack the ability to correctly execute algebraic operations in short periods of time, therefore, we created the calculator to ease our life.
We can demonstrate another example of artificial intelligence, using a rational agent represented by a C# program for solving a sliding tiles puzzle. The rationality of the agent will be provided by an A* search algorithm tied to several heuristics that will help guide the search towards a maximized outcome.
The Puzzle
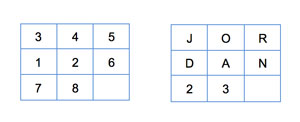
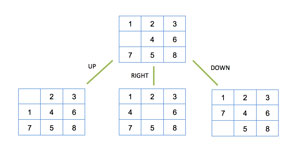
The Sliding Tiles Puzzle was created by chess player and puzzle maker Sam Loyd (1841-1911) in the 1870s. The puzzle consists of a N x M board shown in Figure 1, where each cell could be represented as a number, a letter, an image or basically anything you can think of.
[Click on image for larger view.]
Figure 1: A 3 x 3 Sliding Tiles Puzzles Board
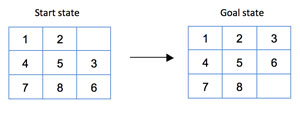
The task in the sliding tiles puzzle is to rearrange the tiles of some starting state in a manner in which all of them end up arranged matching another configuration known as the goal state (see Figure 2).
[Click on image for larger view.]
Figure 2: Moving Tiles from Start State to Goal State
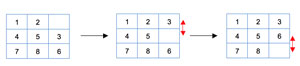
To be able to reach the goal state a sequence of moves is required; one move consists of swapping the empty tile with some other tile. The solution to the previous example would be obtained as shown in Figure 3.
[Click on image for larger view.]
Figure 3: Moving From Start to Goal Requires Moving Two Tiles
A logical question probably pops up into the reader's mind when he thinks of the starting state; could I truly find the goal state from this initial state?
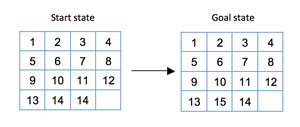
Sam Loyd once offered $1,000 to anyone who could solve the puzzle in Figure 4.
[Click on image for larger view.]
Figure 4: Can You Solve This 4 x 4 Board?
Although several people claimed they found a solution, the reality is that the previous puzzle has no solution. So, how do we know if a given initial configuration is solvable?
It has been proved that a configuration is solvable if the following conditions hold:
-
If the width is odd, every solvable state has an even number of inversions.
-
If the width is even, every solvable state has: a) an even number of inversions if the empty tile is on an odd numbered row counting from the bottom; b) an odd number of inversions if the empty tile is on an even numbered row counting from the bottom.
An inversion occurs when some tile precedes another tile with a lower value; the goal state has zero inversions. For instance, considering a 4 x 4 board the number 12 at the upper left corner will have a total of 11 inversions as numbers 1 through 11 come after it. In general, an inversion is a pair of tiles (a, b) such that a appears before b, but a is greater than b.
The A* algorithm
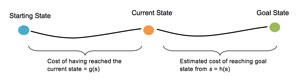
The agent we'll be developing searches the state space (universe of all possible board configurations) using an A* Informed Search (https://en.wikipedia.org/wiki/A*_search_algorithm Hart, 1968). The search is informed as it selects the next step considering domain knowledge which is represented by the value of a function associated to every state of the problem (see Figure 5). The possible states are: up, down, left and right each, related to moving the empty tile in those directions.
[Click on image for larger view.]
Figure 5: A* Informed Search
The key element in the A* resides in the value assigned to every state as it gives the possibility of exponentially reducing the time invested in finding the goal state from a given initial state (see Figure 6). The function outputting the value bound to every state s can be decomposed as:
f(s) = g(s) + h(s)
where g is the cost of reaching s from the initial state, usually translated as the number of moves executed from the initial state up to s and h is the rational component of the agent, the component defining the cost of all possible paths starting at s, this component is known as the heuristic.
[Click on image for larger view.]
Figure 6: Finding Goal State from Given Initial State
The heuristic function is the manner in which we attach our empirical rules to the agent -- therefore, the better rules we add the sooner we'll reach the goal state. The function MisplacedTiles(s) that outputs the number of misplaced tiles for some state s can be considered as a feasible heuristic since it always provides insight on how far we are from reaching the goal state. An important note when creating or including a heuristic is its admissibility, necessary in order to guarantee that the A* algorithm will be complete (it finds a solution) and optimal (it finds an optimal solution).
A heuristic is admissible if it never overestimates the minimum cost of reaching the goal state from some node s, and its value must remain lower or equal than the cost of the shortest path from s to the goal state. The Misplaced Tiles heuristic is admissible since every tile out of place must be moved at least once in order to arrange them into the goal state.
As depicted in the last figure the set of states can be modeled as a graph where the children of a state node are obtained by moving the empty tile in all possible directions. Since the problem can be modeled as a graph it's logical to use a graph search algorithm for locating the goal state.
The basic skeleton of the A* is that of a Breadth First Search. The difference lies on the selection of the next node to enqueue or expand. In a BFS all nodes possess value 1 therefore it does not matter what node to expand -- in the A* we'll always expand the node that maximizes the desired outcome, the node with minimum cost (shortest path to reach the goal state) in the particular case of the Sliding Tiles Puzzle.
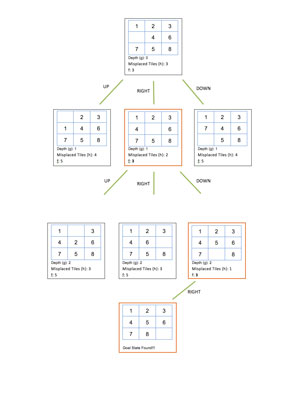
Figure 7 illustrates the execution of the A* algorithm using Misplaced Tiles as heuristic function.
[Click on image for larger view.]
Figure 7: Running the A* Algorithm via Misplaced Tiles
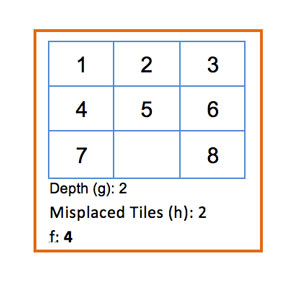
It's important to note when calculating any heuristic that we never take into account the empty tile -- if we do then we could be overestimating the real cost of the shortest path to the goal state, which makes the heuristic non admissible. Consider what would have happened in the prior example if we would have taken into account the empty tile, as shown in Figure 8.
[Click on image for larger view.]
Figure 8: What Happens When We Account For the Empty Tile
In the previous node we are just one step from reaching the goal state but the heuristic claims that we are at least two steps (8 and empty misplaced) from the goal state. It's clearly an overestimation of the real cost, thus, non admissible.
To start analyzing part of the code let us examine the StateNode class in Listing 1 that we'll be using to represent states or configurations on the board.
Listing 1: StateNode Class
class StateNode<T>: IComparable<StateNode<T>> where T: IComparable
{
public double Value { get; set; }
public T[,] State { get; private set; }
public int EmptyCol { get; private set; }
public int EmptyRow { get; private set; }
public int Depth { get; set; }
public string StrRepresentation { get; set; }
public StateNode() { }
public StateNode(T[,] state, int emptyRow, int emptyCol, int depth)
{
if(state.GetLength(0) != state.GetLength(1))
throw new Exception("Number of columns and rows must be the same");
State = state.Clone() as T[,];
EmptyRow = emptyRow;
EmptyCol = emptyCol;
Depth = depth;
for (var i = 0; i < State.GetLength(0); i++)
{
for (var j = 0; j < State.GetLength(1); j++)
StrRepresentation += State[i, j] + ",";
}
}
public int Size
{
get { return State.GetLength(0); }
}
public void Print()
{
for (var i = 0; i < State.GetLength(0); i++)
{
for (var j = 0; j < State.GetLength(1); j++)
Console.Write(State[i,j] + ",");
Console.WriteLine();
}
Console.WriteLine();
}
public int CompareTo(StateNode<T> other)
{
if (Value > other.Value)
return 1;
if (Value < other.Value)
return -1;
return 0;
}
}
The first point to notice in the StateNode class is its generic feature. We are making it generic since we want to have a sliding tiles puzzle with numbers, letters, images, etc. and the T generic type could embody any of the previous types. We are also requiring that the T type be comparable, this can prove to be useful -- even necessary -- if you want to implement a solvability test.
Remember that you'll need to calculate the number of inversions through elements comparisons. Also note that we are assuming the board will have the same width and height (n=m) and that the empty tile is "0". A description of every field, property is presented in this list:
-
Value: represents the value of f = g + h
- T[,] State: the configuration or state represented by this node
- EmptyCol: the column number where the empty tile is located on the board
- EmptyRow: the row number where the empty tile is located on the board
- Depth: depth of this state from the initial state
- StrRepresentation: string representation of the configuration (i.e "1,2,3,4,5,6,7,8,0,". Built upon creation of the object, in the constructor.
The Print() methods prints tiles values on the board in a CSV fashion and the Size property returns the size of the board. Taking into consideration that we inherit from IComparable<StateNode<T>> we need to implement the CompareTo method, and its logic is straightforward. The AStar class is presented in Listing 2.
Listing 2: AStar Class
class AStar<T> where T:IComparable
{
public int StatesVisited { get; set; }
public Dictionary<string, int> PatternDatabase { get; set; }
private readonly StateNode<T> _goal;
private T Empty { get; set; }
private readonly PriorityQueue<StateNode<T>> _queue;
private readonly HashSet<string> _hash;
public AStar(StateNode<T> initial, StateNode<T> goal, T empty)
{
_queue = new PriorityQueue<StateNode<T>>(new[] { initial });
_goal = goal;
Empty = empty;
_hash = new HashSet<string>();
}
public StateNode<T> Execute() ...
private void ExpandNodes(StateNode<T> node) ...
private double Heuristic(StateNode<T> node) ...
private int MisplacedTiles(StateNode<T> node) ...
private int ManhattanDistance(StateNode<T> node) ...
private int LinearConflicts(StateNode<T> node) ...
private int DatabasePattern(StateNode<T> node) ...
private int FindConflicts(T[,] state, int i, int dimension) ...
private int InConflict(int index, T a, T b, int indexA, int indexB, int dimension)...
}
}
Once again a description of each field, property follows:
-
StatesVisited: indicates the number of states visited during the search, equivalent to the number of nodes dequeue.
- PatternDatabase: this dictionary we will be using in the pattern database heuristic, explained shortly.
goal: represents the goal StateNode.
- Empty: represents the empty tile.
- queue: a min-priority queue we'll be using to easily and efficiently get the state node with minimum f value from the set of nodes.
- hashSet: a hash set to store the string representation of every state found.
The sliding tiles puzzle is a cyclic game, starting from some state and after a sequence of moves we could end up in the same state, thus, getting caught up in an infinite loop, we avoid that by saving every visited state in the hash.
Now let us review the Execute() and Expand(StateNode
<T> node) methods in Listings 3 and 4. The rest are all related to heuristics and we'll leave them for the end when we start running the algorithm and making comparisons.
Listing 3: Execute Method
public StateNode<T> Execute()
{
_hash.Add(_queue.Min().StrRepresentation);
while(_queue.Count > 0)
{
var current = _queue.Pop();
StatesVisited++;
if (current.StrRepresentation.Equals(_goal.StrRepresentation))
return current;
ExpandNodes(current);
}
return null;
}
The Execute method is pretty simple. It resembles the body of the BFS algorithm. We add the string representation of the starting state and then get into a loop that ends when _queue has zero nodes. The current variable always holds the node with minimum value and this is the node to be expanded. The expansion consists in all possible moves from the current state.
Listing 4: ExpandNode Method
private void ExpandNodes(StateNode<T> node)
{
T temp;
T[,] newState;
var col = node.EmptyCol;
var row = node.EmptyRow;
StateNode<T> newNode;
// Up
if (row > 0)
{
newState = node.State.Clone() as T[,];
temp = newState[row - 1, col];
newState[row - 1, col] = Empty;
newState[row, col] = temp;
newNode = new StateNode<T>(newState, row - 1, col, node.Depth + 1);
if (!_hash.Contains(newNode.StrRepresentation))
{
newNode.Value = node.Depth + Heuristic(newNode);
_queue.Push(newNode);
_hash.Add(newNode.StrRepresentation);
}
}
// Down
if (row < node.Size - 1)
{
newState = node.State.Clone() as T[,];
temp = newState[row + 1, col];
newState[row + 1, col] = Empty;
newState[row, col] = temp;
newNode = new StateNode<T>(newState, row + 1, col, node.Depth + 1);
if (!_hash.Contains(newNode.StrRepresentation))
{
newNode.Value = node.Depth + Heuristic(newNode);
_queue.Push(newNode);
_hash.Add(newNode.StrRepresentation);
}
}
// Left
if (col > 0)
{
newState = node.State.Clone() as T[,];
temp = newState[row, col - 1];
newState[row, col - 1] = Empty;
newState[row, col] = temp;
newNode = new StateNode<T>(newState, row, col - 1, node.Depth + 1);
if (!_hash.Contains(newNode.StrRepresentation))
{
newNode.Value = node.Depth + Heuristic(newNode);
_queue.Push(newNode);
_hash.Add(newNode.StrRepresentation);
}
}
// Right
if (col < node.Size - 1)
{
newState = node.State.Clone() as T[,];
temp = newState[row, col + 1];
newState[row, col + 1] = Empty;
newState[row, col] = temp;
newNode = new StateNode<T>(newState, row, col + 1, node.Depth + 1);
if (!_hash.Contains(newNode.StrRepresentation))
{
newNode.Value = node.Depth + Heuristic(newNode);
_queue.Push(newNode);
_hash.Add(newNode.StrRepresentation);
}
}
}
In each if statement we check whether the move attempted is possible, if it's then we clone the current state (remember arrays are reference types) and then swap the blank tile with the tile in the position that corresponds to that move. In case the string representation of the newNode hasn't been added to the hash then we enqueue the newNode and add it to the hash. After having described the basic skeleton of the A* algorithm we can now focus on the main component of the search, the heuristics, in Listing 5.
Listing 5: Heuristic Method
private double Heuristic(StateNode<T> node)
{
return DatabasePattern(node);
}
private int MisplacedTiles(StateNode<T> node)
{
var result = 0;
for (var i = 0; i < node.State.GetLength(0); i++)
{
for (var j = 0; j < node.State.GetLength(1); j++)
if (!node.State[i, j].Equals(_goal.State[i, j]) && !node.State[i, j].Equals(Empty))
result++;
}
return result;
}
Heuristic #1: Misplaced Tiles
The first heuristic we'll analyze has already been explained along this article and is probably the simplest of heuristics for this problem: the number of tiles out of place.
Listing 6 shows the laboratory we have set up for testing our heuristics.
Listing 6: Heuristics Lab, Misplaced Tiles
static void Main()
{
var initWorstConfig3x3 = new[,] { {8,6,7},
{2,5,4},
{3,0,1}
};
var initConfig4x4 = new[,] { {5,10,14,7},
{8,3,6,1},
{15,0,12,9},
{2,11,4,13}
};
var finalConfig3x3 = new[,] { {1,2,3},
{4,5,6},
{7,8,0}
};
var finalConfig4x4 = new[,] { {1,2,3,4},
{5,6,7,8},
{9,10,11,12},
{13,14,15,0}
};
var initialState = new StateNode<int>(initWorstConfig3x3, 2, 1, 0);
var finalState = new StateNode<int>(finalConfig3x3, 2, 2, 0);
var watch = new Stopwatch();
var aStar = new AStar<int>(initialState, finalState, 0)
{
PatternDatabase = FillPatternDatabase()
};
watch.Start();
var node = aStar.Execute();
watch.Stop();
Console.WriteLine("Node at depth {0}", node.Depth);
Console.WriteLine("States visited {0}", aStar.StatesVisited);
Console.WriteLine("Elapsed {0} miliseconds", watch.ElapsedMilliseconds);
Console.Read();
}
For testing our heuristics we'll be using one of the worst configurations for a 3x3 board, shown in Figure 9. It requires 31 moves to be completed.
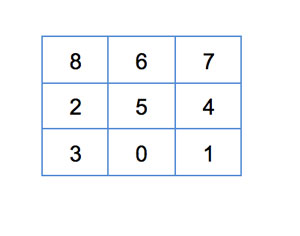[Click on image for larger view.]
Figure 9: A 3 x 3 Board That Requires 31 Moves To Solve
The results obtained are shown in Figure 10.
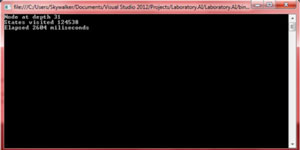[Click on image for larger view.]
Figure 10: Results of Running A* Algorithm on Board in Figure 9
The A* algorithm with the Misplaced Tiles heuristic takes about 2.5 seconds to find the goal state. Let us attempt to find a cleverer heuristic that will lower the time frame and the number of nodes visited.
Heuristic #2: Manhattan Distance
The Manhattan Distance or Block Distance between points A=(x1, y1) and B=(x2, y2) is defined as the sum of the absolute difference of their corresponding coordinates, that is:
MD = |x1-x2| + |y1-y2|
As a heuristic, the Manhattan Distance in Listing 7 is admissible since for each tile it returns the minimum number of steps that will be required to move that tile into its goal position.
Listing 7: Heuristic #2, the Manhattan Distance
private int ManhattanDistance(StateNode<T> node)
{
var result = 0;
for (var i = 0; i < node.State.GetLength(0); i++)
{
for (var j = 0; j < node.State.GetLength(1); j++)
{
var elem = node.State[i, j];
if (elem.Equals(Empty)) continue;
// Variable to break the outer loop and
// avoid unnecessary processing
var found = false;
// Loop to find element in goal state and MD
for (var h = 0; h < _goal.State.GetLength(0); h++)
{
for (var k = 0; k < _goal.State.GetLength(1); k++)
{
if (_goal.State[h, k].Equals(elem))
{
result += Math.Abs(h - i) + Math.Abs(j - k);
found = true;
break;
}
}
if (found) break;
}
}
}
return result;
}
The results applying A* + MD are shown in Figure 11.
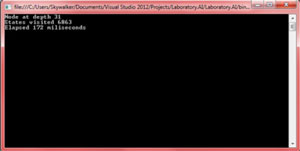[Click on image for larger view.]
Figure 11: Results of A* with Manhattan Distance
The reduction in time and nodes visited is substantial; we are providing better information to guide the search hence the goal is found much quickly.
Heuristic #3: Linear Conflict
The Linear Conflict heuristic provides information on necessary moves that are not counted in by the Manhattan Distance. Two tiles tj and tk are said to be in a linear conflict if tj and tk are in the same line, the goal positions of tj and tk are both in that line, tj is to the right of tk and goal position of tj is to the left of the goal position of tk.
Figure 12 shows tiles 3 and 1 in their corresponding row but reversed.
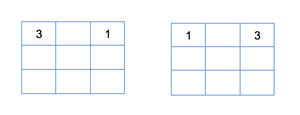[Click on image for larger view.]
Figure 12: The 3 and 1 Tiles Are in The Right Row, Wrong Position
To get them to their goal positions we must move one of them down and then up again, these moves are not considered in the Manhattan Distance. A tile cannot appear related in more than one conflict as solving a determined conflict might imply the resolution of other conflicts in the same row or column. Hence if tile 1 is related to tile 3 in a conflict then it cannot be related to a conflict with tile 2 as this may become an overestimation of the shortest path to a goal state and could turn our heuristic into non admissible. The methods implementing this heuristic are presented in Listing 8.
Listing 8: LinearConflict Method
private int LinearConflicts(StateNode<T> node)
{
var result = 0;
var state = node.State;
// Row Conflicts
for (var i = 0; i < state.GetLength(0); i++)
result += FindConflicts(state, i, 1);
// Column Conflicts
for (var i = 0; i < state.GetLength(1); i++)
result += FindConflicts(state, i, 0);
return result;
}
private int FindConflicts(T[,] state, int i, int dimension)
{
var result = 0;
var tilesRelated = new List<int>();
// Loop foreach pair of elements in the row/column
for (var h = 0; h < state.GetLength(dimension) - 1 && !tilesRelated.Contains(h); h++)
{
for (var k = h + 1; k < state.GetLength(dimension) && !tilesRelated.Contains(h); k++)
{
// Avoid the empty tile
if (dimension == 1 && state[i, h].Equals(Empty)) continue;
if (dimension == 0 && state[h, i].Equals(Empty)) continue;
if (dimension == 1 && state[i, k].Equals(Empty)) continue;
if (dimension == 0 && state[k, i].Equals(Empty)) continue;
var moves = dimension == 1
? InConflict(i, state[i, h], state[i, k], h, k, dimension)
: InConflict(i, state[h, i], state[k, i], h, k, dimension);
if (moves == 0) continue;
result += 2;
tilesRelated.AddRange(new List<int> { h, k });
break;
}
}
return result;
}
private int InConflict(int index, T a, T b, int indexA, int indexB, int dimension)
{
var indexGoalA = -1;
var indexGoalB = -1;
for (var c = 0; c < _goal.State.GetLength(dimension); c++)
{
if (dimension == 1 && _goal.State[index, c].Equals(a))
indexGoalA = c;
else if (dimension == 1 && _goal.State[index, c].Equals(b))
indexGoalB = c;
else if (dimension == 0 && _goal.State[c, index].Equals(a))
indexGoalA = c;
else if (dimension == 0 && _goal.State[c, index].Equals(b))
indexGoalB = c;
}
return (indexGoalA >= 0 && indexGoalB >= 0) && ((indexA < indexB && indexGoalA > indexGoalB) ||
(indexA > indexB && indexGoalA < indexGoalB))
? 2
: 0;
}
To test the Linear Conflict heuristic, we'll use the 4 x 4 board in Figure 13, requiring 55 moves to the goal state. The value of a node s will now be f(s) = depth(s) + md(s) + lc(s). We can combine both heuristics as the moves they represent do not intersect, and consequently we will not be overestimating.
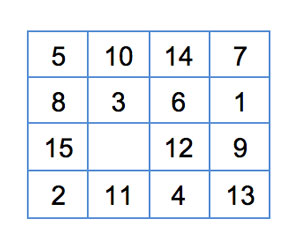[Click on image for larger view.]
Figure 13: 4 x 4 Board for Testing Linear Conflict Heuristic
Figure 14 shows the results.
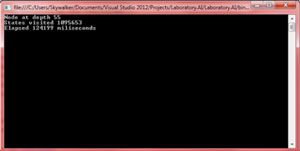[Click on image for larger view.]
Figure 14: Results of Running Linear Conflict
After approximately two minutes the algorithm provided a result. The same board was tested using only the Manhattan Distance and after a 5-minute wait no result had been obtained.
Heuristic #4: Pattern Database
The Pattern Database heuristic in Figure 15 is defined by a database of different states of the game, each state is associated with the minimum number of moves necessary to take a pattern (subset of tiles) to its goal position. In this case we built a small pattern database by making a BFS backwards starting at the goal state (3 x 3). The results were saved in a .txt file of only 60,000 entries. The pattern chosen for the database is known as the fringe -- it contains tiles from the top row and the left most column.
[Click on image for larger view.]
Figure 15: 3 x 3 Board for Running Pattern Database Heuristic
The pattern database heuristic function in Listing 9 is computed by a table look-up function. In this case, it's a dictionary lookup that has 60,000 stored patterns. It philosophically resembles those of the divide and conquer technique and the dynamic programming technique.
Listing 9: Pattern Database Heuristic Function
private int DatabasePattern(StateNode<T> node)
{
var pattern = node.StrRepresentation
.Replace('5', '?')
.Replace('6', '?')
.Replace('7', '?')
.Replace('8', '?');
if (PatternDatabase.ContainsKey(pattern))
return PatternDatabase[pattern];
return ManhattanDistance(node);
}
Figure 16 shows the results.
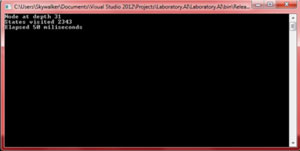[Click on image for larger view.]
Figure 16: Pattern Database Heuristic Results
The more entries we add to the database the lower the time it will take to find the goal state. In this case the compromise between memory and time favors using more memory to get a better running time. This is how it usually works -- you use more memory in order to reduce the execution time.
The pattern database heuristics represents the definitive alternative when you want to solve 4 x 4 puzzles or m x n puzzles where n and m are greater than 3.
The intention of this article was to awake the reader's interest in the amazing world of artificial intelligence and to provide an easy guide into some of the different mechanisms for solving interesting puzzles like these. Build your own pattern database and start solving sliding tiles puzzles in less than 50 milliseconds.