The Data Science Lab
Permutations Using R
R has limited support for mathematical permutations, but it's there. Here's what R is capable of accomplishing.
In this article, I'll show you how to create and manipulate mathematical permutations using the R language. In R, a permutation of order n is one possible rearrangement of the integers 1 through n inclusive. For example, one permutation of order n = 5 is (3, 5, 1, 4, 2). Note that because most other programming languages use 0-based array indexing instead of the 1-based indexing used by R, in other languages a permutation of order n is one possible arrangement of the integers 0 through n-1 inclusive.
To get an idea of where this article is headed, take a look at the demo R session in Figure 1.
The outer container window is the Rgui.exe shell. Inside the shell, the window on the left is the R Console where you can issue interactive commands. I use the special R incantation rm(list=ls()) to remove all existing objects in the current workspace. Then I use the setwd function to set the working directory to the location of my demo R file, and then I use the source function to execute the perms.R demo script.
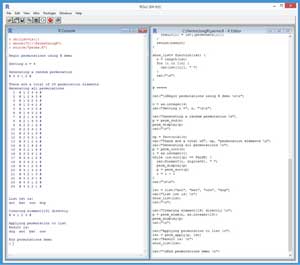 [Click on image for larger view.]
Figure 1. Permutations with R Demo Session
[Click on image for larger view.]
Figure 1. Permutations with R Demo Session
Installing R
If you don't have R on your system, installing R (and uninstalling) is very easy. Do an Internet search for "Install R" and you'll find a page on the cran.r-project.org Web site with a link labeled "Download R 3.x.y for Windows." Click that link and you'll get an option to run a self-extracting installer file named something like R-3.x.y-win.exe. Click on the Run button presented to you by your browser to launch the installer. You can accept all the configuration defaults and installation is very quick. The demo program (technically a script because R is interpreted) uses R version 3.4.2, but any 3.x version will work.
To launch the Rgui program, open a file explorer and navigate to the C:\Program Files\R\R-3.x.y\bin\x64 directory. Then double-click on file Rgui.exe and the Rgui shell with an R Console window will launch. On some systems you'll need to right-click and select "Run as administrator" from the context menu. You can clear the startup messages in the Console window with a Ctrl+L.
To create the demo script, I clicked File | New Script on the Rgui menu bar. This gave me an editor window. I clicked File | Save As and saved the (currently empty) script as perms.R in directory C:\PermsUsingR on my machine. The complete code for script perms.R is presented in Listing 1.
Listing 1: Permutations Demo Code
# R 3.4.2
# file: perms.R
perm_init = function(n) {
result = list(data = c(1:n), n = n)
return(result)
}
perm_rnd = function(n) {
result = perm_init(n)
result$data = sample(1:n)
return(result)
}
perm_display = function(perm) {
n = perm$n
cat("# " )
for (i in 1:n) {
cat(perm$data[i], " ", sep="")
}
cat("# \n")
}
perm_succ = function(perm) {
n = perm$n
result = perm_init(n)
result$data = perm$data
left = n - 1
while (result$data[left] > result$data[left+1]
&& left >= 2) {
left = left - 1
}
if (left == 1 && result$data[left] >
result$data[left+1]) {
return(NULL)
}
right = n
while (result$data[left] >
result$data[right]) {
right = right - 1
}
tmp = result$data[left]
result$data[left] = result$data[right]
result$data[right] = tmp
i = left + 1; j = n
while (i < j) {
tmp = result$data[i]
result$data[i] = result$data[j]
result$data[j] = tmp
i = i + 1; j = j - 1
}
return(result)
} # perm_succ
perm_elem = function(n, i) {
# ith element of perm order n
p = perm_init(n)
for (j in 1:(i-1)) {
p = perm_succ(p)
}
return(p)
}
perm_apply = function(perm, lst) {
result = list()
n = perm$n
for (i in 1:n) {
result[i] = lst[[perm$data[i]]]
}
return(result)
}
show_list= function(lst) {
n = length(lst)
for (i in 1:n) {
cat(lst[[i]], " ")
}
cat("\n")
}
# =====
cat("\nBegin permutations using R demo \n\n")
n = 4
cat("Setting n =", n, "\n\n")
cat("Generating a random permutation \n")
p = perm_rnd(n)
perm_display(p)
cat("\n")
np = factorial(n)
cat("There are ", np, "elements \n")
cat("Generating all permutations \n")
p = perm_init(n)
i = as.integer(1)
while (is.null(p) == FALSE) {
cat(formatC(i, digits=2), " ")
perm_display(p)
p = perm_succ(p)
i = i + 1
}
cat("\n\n")
lst = list("ant", "bat", "cow", "dog")
cat("List lst is: \n")
show_list(lst)
cat("\n")
cat("Creating element[19] directly \n")
p = perm_elem(n, 19)
perm_display(p)
cat("\n")
cat("Applying permutation to list \n")
lst = perm_apply(p, lst)
cat("Result is: \n")
show_list(lst)
cat("\nEnd permutations demo \n")
Permutation Initialization
The first few lines of code in the demo script are:
# R 3.4.2
# file: perms.R
perm_init = function(n) {
result = list(data = c(1:n), n = n)
return(result)
}
After commenting the name of the script and the version of R, I define a perm_init function. A permutation has an order n and a vector to hold integers 1 through n. An R vector is equivalent to an array in most other programming languages. There are three main ways to encapsulate items in R. You can put the items in a list, or in an S3 or S4 class, or in an R6 class. Here, I use a list, the simplest technique.
The list vector member is named data. I could've used "values" or any other legal R identifier. The call to the tersely named c function creates an integer vector with values 1 through n. In C#, you'd write something like int[] data = new int[] { 1, 2, 3, 4 }. The statement n = n might look a bit strange to you. The n on the right side of the assignment is the function parameter. The n on the left side is a list member name.
In R you can use either "=" or "<-" for assignment. R purists tend to prefer "<-" because that's what was used in the S language, the predecessor of R. As R has become more mainstream, the use of "=" is increasing. I prefer "=" because it's easier to type than "<-".
After defining an initiation function, the demo script defines a function to generate a random permutation and a function to display a permutation. The random permutation function definition is:
perm_rnd = function(n) {
result = perm_init(n)
result$data = sample(1:n)
return(result)
}
Function perm_rnd uses the built-in R sample function, which generates random integers. The sample function is essentially the only built-in R function for permutations.
The display function definition is:
perm_display = function(perm) {
n = perm$n
cat("# " )
for (i in 1:n) {
cat(perm$data[i], " ", sep="")
}
cat("# \n")
}
Function perm_display uses a for-loop to iterate through the data vector. The call to the cat function prints a single blank space after each item and specifies no additional space between items with the sep parameter. Because the default separator is a single blank space, the statement could've been written as cat(perm$data, "").
The demo script code that calls the initialization and display functions is:
n = as.integer(4)
cat("Setting n =", n, "\n\n")
cat("Generating a random permutation \n")
p = perm_rnd(n)
perm_display(p)
cat("\n")
The call to perm_rnd will generate a different random permutation every time the demo script is run. If you want to get reproducible results, you can set the system random number generator seed by issuing a statement like set.seed(0). Here, 0 is the seed value and is arbitrary. Note that unlike most programming languages, R uses the "." character rather than "_" as a way to make function and variable names more readable.
Permutation Successor Function
A key function when working with permutations is one that generates the successor to a given permutation. A successor function allows you to generate all possible permutations. Suppose n = 3. There are 6 different permutations:
(1, 2, 3)
(1, 3, 2)
(2, 1, 3)
(2, 3, 1)
(3, 1, 2)
(3, 2, 1)
Here, the permutations are listed in what's called lexicographical order. One way to think of lexicographical order is that if each permutation is imagined as an integer, then the permutations are in ordinary numeric order. That is, 123 < 132 < 213 < . . . < 321.
There are n! (n factorial) different permutations of order n. For example, if n = 4, there are 4 * 3 * 2 * 1 = 24 different permutations as shown in Figure 1. If n = 5, there are 5 * 4 * . . . * 1 = 120 different permutations, and so on.
Generating the successor to a given permutation is quite interesting. The demo program implements a lexicographical successor as the perm_succ function in Listing 1. The definition of the function begins with:
perm_succ = function(perm) {
n = perm$n
result = perm_init(n)
result$data = perm$data
The first statements create a copy of the input parameter permutation. Next is:
left = n - 1
while (result$data[left] > result$data[left+1] && left >= 2) {
left = left - 1
}
The basis of the successor algorithm is to identify the indices of two key values in the permutation. These key indices are named left and right. Index left starts at the next-to-last cell of the data vector (recall R vectors are 1-based, not 0-based) and moves to the left. I'll explain in more detail shortly.
At this point, it's possible to determine if the input permutation is the last permutation:
if (left == 1 && result$data[left] > result$data[left+1]) {
return(NULL)
}
Suppose n = 4. Then the last permutation in lexicographical order is (4, 3, 2, 1). In general, the last permutation of order n will be (n, n-1, . . . , 1) so you could check to see if the items in the data vector are in reverse order. However, this is an expensive operation and the this last code snippet is much more efficient because it involves only two comparisons. If the input permutation is the last permutation, function perm_succ returns NULL, which is similar to null in other languages.
Next, the right index is found:
right = n
while (result$data[left] > result$data[right]) {
right = right - 1
}
Here, index right starts at the last cell of the data vector and moves to the left. At this point, indices left and right will be pointing at two key cells of the data vector. Next, the values at indices left and right are swapped:
tmp = result$data[left]
result$data[left] = result$data[right]
result$data[right] = tmp
In R, you swap two values in a vector just as you would in most other programming languages (with the notable exception of Python, which has clever syntax to do so).
Function perm_succ finishes by reversing the order of all the items in the data vector that are to the right of index left:
i = left + 1; j = n
while (i < j) {
tmp = result$data[i]
result$data[i] = result$data[j]
result$data[j] = tmp
i = i + 1; j = j - 1
}
return(result)
} # end function
In R, a statement is terminated by the newline character, but you can place multiple statements on a single line by using the semicolon character as I've done here.
The successor algorithm is best explained by example. Suppose some permutation of order n = 7 is:
(7, 4, 6, 5, 3, 2, 1)
The target successor you want to generate is (7, 5, 1, 2, 3, 4, 6). Index left is the index where [left] > [left+1] so here left = 2 (pointing to value 4). Index right is the index where [right] > [left] so here right = 4 (pointing to value 5). The values at left and right are swapped giving an intermediate result of:
(7, 5, 6, 4, 3, 2, 1)
After the swap, all the values to the right of index left, (6, 4, 3, 2, 1), are reversed, (1, 2, 3, 4, 6), giving the final result of (7, 5, 1, 2, 3, 4, 6).
The calling statements that use function perm_succ begin with:
np = factorial(n)
cat("There are a total of", np, "permutation elements \n")
cat("Generating all permutations \n")
Function factorial is a built-in R function. The maximum integer in R on your machine can be found with .Machine$integer.max and is typically 2^32 - 1 = 2,147,483,647. Because R has no built-in big integer type, factorial returns a type double, which you could verify by entering typeof(np). The lack of a big integer type is a significant weakness of R, but you can get big integer functionality with the GNU Multiple Arithmetic (gmp) add-on package.
The demo program statements that generate all permutations of order n = 4 are:
p = perm_init(n)
i = as.integer(1)
while (is.null(p) == FALSE) {
cat(formatC(i, digits=2), " ")
perm_display(p)
p = perm_succ(p)
i = i + 1
}
There's quite a bit going on in these few lines of code. Counter variable i is explicitly coerced to an integer using the as.integer function because the default numeric type in R is type double. In R you can't directly compare an object to NULL using the "==" operator, so you must use the is.null function. I use the formatC function to line up the values of the i counter variable in the display.
Using Permutations
In most R programming situations, permutations represent vector or list indices. The demo program defines a function that generates a specific permutation and a function that applies a given permutation to a list of objects.
Function perm_elem is defined as:
perm_elem = function(n, i) {
# ith element of perm order n
p = perm_init(n)
for (j in 1:(i-1)) {
p = perm_succ(p)
}
return(p)
}
The function creates the first permutation of order n and then iterates using perm_succ until it reaches the target permutation. This is a very crude approach and is feasible only when i is relatively small (less than 1,000,000). It's possible to write a very sophisticated perm_elem function that generates the ith permutation of order n directly using a remarkable idea called the factoradic of a number. You can find information about the factoradic by doing an Internet search.
Function perm_apply is defined:
perm_apply = function(perm, lst) {
result = list()
n = perm$n
for (i in 1:n) {
result[i] = lst[[perm$data[i]]]
}
return(result)
}
The function creates an empty list and then builds up the desired items from an input list. Notice the double square bracket notation. This is a quirk of R that often trips up beginners. When accessing a list element by index, if you use single square brackets the result is a list. If you use double square brackets the result is an object in the list.
The code in the demo program that calls the create functions is:
cat("Creating element[19] directly \n")
p = perm_elem(n, as.integer(19))
perm_display(p)
The code in the demo program that calls the apply function is:
cat("Applying permutation to list \n")
lst = perm_apply(p, lst)
cat("Result is: \n")
show_list(lst)
Function show_list is a program-defined function and it's presented in Listing 1.
Wrapping Up
The explanation presented in this article should give you all the information you need to get up and running with mathematical permutations in R. Permutations are closely related to combinations. A mathematical combination of order (n, k) is one possible subset of k items from n items. For example, the first two combinations and the last combination of order n = 7 and k = 4 are:
(1, 2, 3, 4)
(1, 2, 4, 3)
. . .
(4, 5, 6, 7)
Collectively, the study of permutations and combinations is called combinatorics. Permutations and combinations have many important applications in machine learning and security. An important class of problems is called combinatorial optimization. In a combinatorial optimization problem, the goal is to find the best permutation or combination. The traveling salesman problem (TSP) is the most famous combinatorial optimization problem and I'll show you how to solve TSP in a future article.