The Data Science Lab
The Traveling Salesman Problem Using an Evolutionary Algorithm with C#
Dr. James McCaffrey of Microsoft Research uses full code samples to detail an evolutionary algorithm technique that apparently hasn't been published before.
The goal of a combinatorial optimization problem is to find a set of distinct integer values that minimizes some cost function. The most famous example is the Traveling Salesman Problem (TSP). There are several variations of TSP. The screenshot in Figure 1 shows a version where there are 20 cities, numbered from 0 to 19. The goal is to start at any city then visit all cities in such a way that minimizes the total distance traveled. The problem is artificial and designed so that the optimal solution is (0, 1, . . 19) with a total distance of 19.0 units.
Combinatorial optimization problems are among the most difficult in computer science. One of the most common techniques for solving them is an old approach called simulated annealing. This article presents a new approach for solving TSP called an evolutionary algorithm.
An evolutionary algorithm loosely mimics biological crossover (combining two existing parent solutions to create a new child solution) and mutation (slightly modifying a solution in a random way). In high-level pseudo-code:
create population of random solutions
loop many times
pick two parent solutions
create a child solution
mutate child
evaluate child
replace weak solution in pop with child
end-loop
return best solution found
The demo program in Figure 1 sets up a population of six random solutions. After 1,000 iterations of crossover and mutation, the demo returns a good, but not optimal, solution of (0, 1, 2, 5, 14, . . 9, 7) with a total distance of 67.0 units.
 [Click on image for larger view.] Figure 1: Traveling Salesman Problem Using an Evolutionary Algorithm in Action
[Click on image for larger view.] Figure 1: Traveling Salesman Problem Using an Evolutionary Algorithm in Action
This article assumes you have intermediate or better programming skill but doesn't assume you know anything about evolutionary algorithms. The demo is implemented using C# but you should have no trouble refactoring the code to a different C-family language if you wish.
The complete source code for the demo program is presented in this article and as a downloadable attachment. The code is also available online.
Overall Program Structure
I used Visual Studio 2022 (Community Free Edition) for the demo program. I created a new C# console application and checked the "Place solution and project in the same directory" option. I specified .NET version 6.0. I named the project TSP_Evolutionary. I checked the "Do not use top-level statements" option to avoid the confusing program entry point shortcut syntax.
The demo has no significant .NET dependencies and any relatively recent version of Visual Studio with .NET (Core) or the older .NET Framework should work fine. You can also use the Visual Studio Code program if you like.
After the template code loaded into the editor, I right-clicked on file Program.cs in the Solution Explorer window and renamed the file to the more descriptive TSP_EvoProgram.cs. I allowed Visual Studio to automatically rename class Program to TSP_EvoProgram.
The overall program structure is presented in Listing 1. The heart of the demo program is a Solver class with a Solve() method.
Listing 1: Overall Program Structure
using System;
namespace TSP_Evolutionary
{
internal class TSP_EvoProgram
{
static void Main(string[] args)
{
Console.WriteLine("Begin evolutionary optimization ");
Console.WriteLine("Setting TSP n = 20 cities ");
Console.WriteLine("20! = 2,432,902,008,176,640,000 ");
Console.WriteLine("Opt soln is 0 . . 19 dist = 19 ");
int numCities = 20;
int numPop = 6;
double[][] distances = GetDistances(numCities);
Solver solver = new Solver(numCities, numPop,
distances, seed: 99);
Console.WriteLine("Initial population: ");
solver.Show();
Console.WriteLine("Begin search ");
solver.Solve(1000);
Console.WriteLine("Done ");
Console.WriteLine("Final population: ");
solver.Show();
Console.WriteLine("End demo ");
Console.ReadLine();
} // Main()
static double[][] GetDistances(int n)
{
// in non-demo, these come from a file
double[][] result = new double[n][];
for (int i = 0; i < n; ++i)
result[i] = new double[n];
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
if (i < j) result[i][j] = (j - i) * 1.0;
else if (i > j) result[i][j] = (i - j) * 1.5;
return result;
}
} // Program
class Solver
{
public Random rnd;
public int numCities;
public int numPop; // should be even
public double[][] distances;
public int[][] pop; // array of solns[]
public double[] errs;
public int[] bestSoln;
public double bestErr;
public Solver(int numCities, int numPop,
public void Show() { . . }
public void Shuffle(int[] soln) { . . }
public double ComputeError(int[] soln) { . . }
public int[] MakeChild(int idx1, int idx2) { . . }
public void Mutate(int[] soln) { . . }
public void Solve(int maxGen) { . . }
}
} // ns
In the Main() method, the Solver object is instantiated for a population of six random solutions, each of which is a vector with 20 integer values. The population size value is a hyperparameter that must be determined by experimentation.
The dummy distances between each pair of cities are supplied by a GetDistances() function. If city A is less than city B, then dist(A, B) = B - A, for example, dist(3, 7) = 4.0 units. If city A is greater than city B, then dist(A, B) = 1.5 * (A - B), for example, dist(11, 8) = 1.5 * (11 - 8) = 4.5 units. In a non-demo scenario you'd likely read the distances between cities from a text file.
The Solve() method performs the evolutionary algorithm using maxGen = 1,000 generations. The value of maxGen is a hyperparameter. The Solver class methods are declared with public scope to make it easier to refactor the C# demo code to a language that doesn't support private scope.
The Solver Class
The Solver class constructor code is presented in Listing 2. Because evolutionary algorithms use random operations for crossover and mutation, the Solver class uses a Random object member rather than relying on a global Random object. The pop (population) member is an array of arrays, for example, pop[2][3] is the value/city of solution [2] at index [3].
Listing 2: The Solver Class Constructor
public class Solver
{
public Random rnd;
public int numCities;
public int numPop; // should be even
public double[][] distances;
public int[][] pop; // array of solns[]
public double[] errs;
public int[] bestSoln;
public double bestErr;
public Solver(int numCities, int numPop,
double[][] distances, int seed)
{
this.rnd = new Random(seed);
this.numCities = numCities;
this.numPop = numPop;
this.bestErr = 0.0;
this.distances = distances;
this.pop = new int[numPop][]; // allocate
for (int i = 0; i < numPop; ++i)
this.pop[i] = new int[numCities];
this.errs = new double[numPop];
for (int i = 0; i < numPop; ++i) // init
{
for (int j = 0; j < numCities; ++j) {
this.pop[i][j] = j; // [0, 1, 2, . . ]
}
this.Shuffle(this.pop[i]);
this.errs[i] = this.ComputeError(this.pop[i]);
}
Array.Sort(this.errs, this.pop); // parallel sort by err
this.bestSoln = new int[numCities];
for (int j = 0; j < this.numCities; ++j)
this.bestSoln[j] = this.pop[0][j];
this.bestErr = this.errs[0];
} // ctor
// other Solver methods here
}
The errs member is a vector that holds the error for each solution in the population. For simplicity, the design of the Solver class uses parallel arrays for the population of solutions and the associated errors. An alternative design is to create a program-defined class object that holds a vector/solution and its associated error.
Each random solution is generated by placing values 0 through 19 in an array and then shuffling the values using a program-defined Shuffle() method which implements the Fisher-Yates algorithm:
public void Shuffle(int[] soln)
{
int n = soln.Length;
for (int i = 0; i < n; ++i) {
int ri = this.rnd.Next(i, n); // random index
int tmp = soln[ri];
soln[ri] = soln[i];
soln[i] = tmp;
}
}
The bestSoln member is a vector that holds the best solution found at any point by the Solve() method. The bestErr value is the associated best (lowest) error/distance.
After the initial values of the population and errors vectors have been assigned, the constructor sorts both in parallel, from smallest error to largest, using the built-in Array.Sort() method. After sorting, the best solution is at pop[0] and its error is at errs[0]. These values are copied to the bestSoln and bestErr members.
Computing Error
The demo computes the error/distance for a solution using a ComputeError() method:
public double ComputeError(int[] soln)
{
double d = 0.0; // total distance between cities
int n = soln.Length; // aka numCities
for (int i = 0; i < n - 1; ++i) {
int fromCity = soln[i]; int toCity = soln[i + 1];
d += this.distances[fromCity][toCity];
}
return d;
}
The ComputeError() method walks through each pair of city values in a solution and looks up the distance between the cities in the this.distances matrix. The distances matrix is created by the GetDistances() function and then passed to the Solver constructor where it is copied by reference.
The Solver class implements a Show() method that displays the solutions in the population and the best solution currently found. The Show() method is presented in Listing 3.
Listing 3: The Show() Method
public void Show()
{
for (int i = 0; i < this.numPop; ++i) {
for (int j = 0; j < this.numCities; ++j) {
Console.Write(this.pop[i][j] + " ");
}
Console.WriteLine(" | " + this.errs[i].ToString("F4"));
}
Console.WriteLine("-----");
for (int j = 0; j < this.numCities; ++j)
Console.Write(this.bestSoln[j] + " ");
Console.WriteLine(" | " + this.bestErr.ToString("F4"));
}
The best solution is determined by visually examining the output of the Show() method. An alternative design is for the Solve() method to return the best solution found.
Crossover and Mutation
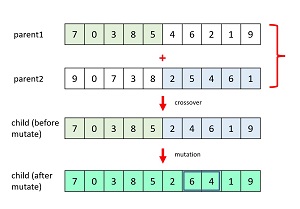
The crossover and mutation operations are illustrated in Figure 2. The crossover mechanism combines two parent solutions to create a new, hopefully better, child solution. The first step is to pick two parent indices from the existing population.
 [Click on image for larger view.] Figure 2: Crossover and Mutation
[Click on image for larger view.] Figure 2: Crossover and Mutation
The demo program uses the simple approach of picking one parent index from the top/best half of the population and the other parent index from the other half of the population. The next challenge is to combine half of the first parent with half of the second parent in a way that keeps characteristics of both parents but generates a legal solution where each city appears only once.
In Figure 2, parent1 = (7, 0, 3, 8, 5, 4, 6, 2, 1, 9) and parent2 = (9, 0, 7, 3, 8, 2, 5, 4, 6, 1). If you naively take the left half of parent1 and the right half of parent2 you get a child of (7, 0, 3, 8, 5, 2, 5, 4, 6, 1), which isn't a legal solution because the child has two 5 values and no 9 value.
The demo program combines two parent solutions by taking the left half of parent1 then walking through the right half of parent2, using each value in parent2 only if it hasn't appeared in the child yet. If necessary, the child uses values from the left half of parent2. The method implementation is shown in Listing 4.
Listing 4: The MakeChild() Method
public int[] MakeChild(int idx1, int idx2) // crossover
{
int[] parent1 = this.pop[idx1];
int[] parent2 = this.pop[idx2];
int[] result = new int[this.numCities];
int[] used = new int[this.numCities];
int[] candidates = new int[2 * this.numCities];
int k = 0;
for (int i = 0;
i < this.numCities / 2; ++i) // left of parent1
{
candidates[k++] = parent1[i];
}
for (int i = this.numCities / 2;
i < this.numCities; ++i) // right parent2
{
candidates[k++] = parent2[i];
}
for (int i = 0;
i < this.numCities / 2; ++i) // left parent2
{
candidates[k++] = parent2[i];
}
for (int i = this.numCities / 2;
i < this.numCities; ++i) // never used for TSP
{
candidates[k++] = parent1[i];
}
k = 0;
for (int i = 0; i < this.numCities; ++i)
{
while (used[candidates[k]] == 1) // to an unused
k += 1;
result[i] = candidates[k];
used[candidates[k]] = 1;
}
return result;
} // MakeChild()
The crossover point is the middle value in each parent. There are many more complicated ways to implement crossover, but the simple approach used in the demo is usually effective in my experience.
The Mutate() method selects a random index that points into the newly created child and swaps values at [idx] and [idx+1].
public void Mutate(int[] soln)
{
int idx = this.rnd.Next(0, this.numCities - 1);
int tmp = soln[idx];
soln[idx] = soln[idx+1];
soln[idx+1] = tmp;
}
There are many alternative strategies for the mutation operation, but the simple approach used by the demo works well.
The Solve() Method
The heart of the demo program is the Solve() method. The implementation begins with:
public void Solve(int maxGen)
{
for (int gen = 0; gen < maxGen; ++gen)
{
// 1. pick parent indexes
int idx1, idx2;
int flip = this.rnd.Next(2);
. . .
A virtual coin flip determines which index into the population will be used as parent1 and which will be used as parent2:
if (flip == 0) {
idx1 = this.rnd.Next(0, this.numPop / 2);
idx2 = this.rnd.Next(this.numPop / 2, this.numPop);
}
else {
idx2 = this.rnd.Next(0, this.numPop / 2);
idx1 = this.rnd.Next(this.numPop / 2, this.numPop);
}
The idea here is that half of the time you want parent1 to be one of the top/best existing solutions and sometimes you want parent1 to be one of the bottom/worst existing solutions. Next, the child solution is created:
// 2. create a child
int[] child = MakeChild(idx1, idx2);
Mutate(child);
double childErr = this.ComputeError(child);
The newly created child is checked to see if it is the best solution found so far:
// 3. found new best?
if (childErr < this.bestErr)
{
Console.WriteLine("New best soltn at gen " + gen);
for (int j = 0; j < child.Length; ++j)
this.bestSoln[j] = child[j];
this.bestErr = childErr;
}
The new child replaces a randomly selected solution in the bottom/worst half of the population:
// 4. replace weak soln
int idx = this.rnd.Next(this.numPop / 2, this.numPop);
this.pop[idx] = child;
this.errs[idx] = childErr;
The replacement is done using copy-by-reference, but copy-by-value is possible too. Next, the demo uses an optional immigrant technique to create a new, random solution:
// 5. create an immigrant
int[] imm = new int[this.numCities];
for (int j = 0; j < this.numCities; ++j)
imm[j] = j;
this.Shuffle(imm);
double immErr = this.ComputeError(imm);
An immigrant solution is created using the same mechanism as initial population solutions. The immigrant must be checked to see if it is a new best solution:
// found new best?
if (immErr < this.bestErr) {
Console.WriteLine("Best (immigrant) at gen " + gen);
for (int j = 0; j < imm.Length; ++j)
this.bestSoln[j] = imm[j];
this.bestErr = immErr;
}
Regardless of whether or not the immigrant was a new best solution, the immigrant replaces a weak solution in the bottom half of the population:
// 4. replace weak soln
idx = this.rnd.Next(this.numPop / 2, this.numPop);
this.pop[idx] = imm;
this.errs[idx] = immErr;
After child and immigrant solution have been placed into the population, the population is sorted from small error/distance to largest:
. . .
// 5. sort the new population
Array.Sort(this.errs, this.pop);
} // gen
} // Solve()
The built-in C# Array.Sort() method can sort parallel arrays -- a nice feature that isn't available in most programming languages.
Wrapping Up
Combinatorial optimization problems are surprisingly difficult. For the demo problem with only 20 cities, there are 20! = 2,432,902,008,176,640,000 possible solutions and therefore randomly searching for a good solution is unlikely to give a good result.
To the best of my knowledge, the technique using an evolutionary algorithm presented in this article hasn't been published before. When compared to other algorithms such as simulated annealing, the evolutionary algorithm approach tends to work better, meaning it gives a better solution for a similar amount of computation.