The Data Science Lab
Decision Tree Regression from Scratch Using C#
Dr. James McCaffrey of Microsoft Research says the technique is easy to tune, works well with small datasets and produces highly interpretable predictions, but there are also trade-off cons.
The goal of a machine learning regression problem is to predict a single numeric value. For example, you might want to predict the annual income of a person based on their sex (male or female), age, State of residence, and political leaning (conservative, moderate, liberal).
There are roughly a dozen major regression techniques, and each technique has several variations. Among the most common techniques are linear regression, linear ridge regression, k-nearest neighbors regression, kernel ridge regression, Gaussian process regression, decision tree regression, and neural network regression. Each technique has pros and cons. This article explains how to implement decision tree regression from scratch, using the C# language.
Compared to other regression techniques, decision tree regression is easy to tune, works well with small datasets and produces highly interpretable predictions. However, decision tree regression is extremely sensitive to changes in the training data, and it is susceptible to model overfitting.
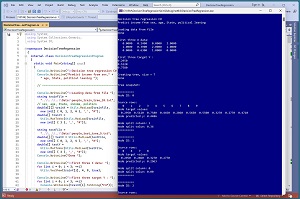
A good way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. The demo program uses a tiny 10-item dataset of training data and a 5-item test dataset where the data looks like:
0, 0.24, 0, 0.2950, 2
1, 0.39, 2, 0.5120, 1
0, 0.63, 1, 0.7580, 0
. . .
The fields are sex, age, State, income, political leaning. The goal is to predict income from the other four variables.
The demo program creates a decision tree regression model where the tree has seven nodes. After the tree is created, the demo program computes the model accuracy on the training data as 0.9000 (9 out of 10 correct) and the accuracy of the model on a tiny five-item test dataset as 0.2000 (1 out of 5 correct).
The demo program concludes by predicting the income for a new, previously unseen person who is male, age 34, lives in Oklahoma, and is a political moderate. The predicted income is $28,600.
 [Click on image for larger view.] Figure 1: Decision Tree Regression in Action
[Click on image for larger view.] Figure 1: Decision Tree Regression in Action
This article assumes you have intermediate or better programming skill but doesn't assume you know anything about decision tree regression. The demo is implemented using C#, but you should be able to refactor the code to a different C-family language if you wish.
The source code for the demo program is too long to be presented in its entirety in this article. The complete code is available in the accompanying file download. The demo code is also available online.
Understanding the Data
Decision tree prediction systems can be implemented in many different ways. The general principles are best understood by examining a concrete example. The demo program uses a tiny 10-item training dataset:
[0] 0, 0.24, 0, 0.2950, 2
[1] 1, 0.39, 2, 0.5120, 1
[2] 0, 0.63, 1, 0.7580, 0
[3] 1, 0.36, 0, 0.4450, 1
[4] 0, 0.27, 1, 0.2860, 2
[5] 0, 0.50, 1, 0.5650, 1
[6] 0, 0.50, 2, 0.5500, 1
[7] 1, 0.19, 2, 0.3270, 0
[8] 0, 0.22, 1, 0.2770, 1
[9] 1, 0.39, 2, 0.4710, 2
The row indices, from [0] to [9], are shown but are not explicitly stored in the data file. The fields are sex (male = 0, female = 1), age (divided by 100), State (Michigan = 0, Nebraska = 1, Oklahoma = 2), income (divided by $100,000), and political leaning (conservative = 0, moderate = 1, liberal = 2). The goal is to predict income from sex, age, State and political leaning.
For the decision tree presented in this article, categorical predictors, such as sex, State and political leaning, should be zero-based integer-encoded. Because the tree-building algorithm computes the overall statistical variance of different partitions of the training data, the numeric predictors should be normalized. This prevents predictors with large magnitudes, such as income, from dominating the variance. The demo doesn't use any ordinal data (such as a height predictor with values short, medium, tall), but if you have ordinal data it should be zero-based integer encoded.
Understanding Decision Tree Regression
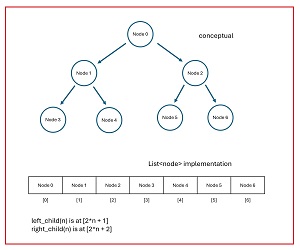
A decision tree is similar to a binary search tree. The demo decision tree implementation creates a tree with a fixed number of nodes. The implementation stores nodes in a C# List. See the image in Figure 2. The demo decision tree has 7 nodes. Because of the binary structure, the number of nodes should be 2^n - 1, for example, 7, 15, 31, 63, 127, and so on.
 [Click on image for larger view.] Figure 2: Decision Tree Implementation
[Click on image for larger view.] Figure 2: Decision Tree Implementation
Tree node [0] holds all 10 source rows, [0] through [9]. The associated target income values are (0.2950, 0.5120, 0.7580, 0.4450, 0.2860, 0.5650, 0.5500, 0.3270, 0.2770, 0.4710). Without any additional information, the predicted income is the average of the target values: 0.4486.
The tree construction algorithm examines every value in every column. Each value creates a partition of two sets of data rows. The tree is constructed so that the average statistical variance of the partition is minimized. For the demo data, in node [0] the split column is [1] (age) and the split value is 0.36. Data rows that have an age value strictly less than 0.36 are placed into the left child node [1]. Data rows that have age greater than or equal to 0.36 are placed into the right child node [2].
After splitting, tree node [1] holds four rows: 0, 4, 7, 8. Tree node [2] holds the other six rows. The target values in node [1] are (0.2950, 0.2860, 0.3270, 0.2770) and so at this point the decision rule is "IF column 1 (age) less-than 0.36" and the predicted income is their average: 0.2963. The values in rows 0, 4, 7, 8 are examined and the value that minimizes partition variance is 0 (male) in column [0]. All the rows that are not equal to the split value 0 are placed in the left child, node [3], and all the rows that are equal to the split value are placed in the right child node [4].
The partitioning process continues until there are no more empty nodes to accept information. Notice that partitioning depends on whether the split value is numeric or categorical. If the split value is numeric, then the criterion is less-than to the left and greater-than-or-equal to the right. If the split value is categorical, then the criterion is not-equal to the left and is-equal to the right. Because the split criterion depends on data type, the decision tree object must be passed column type information.
Overall Program Structure
I used Visual Studio 2022 (Community Free Edition) for the demo program. I created a new C# console application named DecisionTreeRegression and checked the "Place solution and project in the same directory" option. I specified .NET version 6.0. I checked the "Do not use top-level statements" option to avoid the program entry point shortcut syntax.
The demo program has no significant .NET dependencies and any relatively recent version of Visual Studio with .NET (Core) or the older .NET Framework will work fine. You can also use the Visual Studio Code program if you like.
After the template code loaded into the editor, I right-clicked on file Program.cs in the Solution Explorer window and renamed the file to the more descriptive DecisionTreeRegressionProgram.cs. I allowed Visual Studio to automatically rename class Program.
The overall program structure is presented in Listing 1. The demo program has three primary classes. The Program class holds all the control logic. The DecisionTree class houses all the tree functionality. It has two nested helper classes, Node and SplitInfo. The Utils class houses functionality to load data from file into memory.
Listing 1: Overall Program Structure
using System;
using System.Collections.Generic;
using System.IO;
namespace DecisionTreeRegression
{
internal class DecisionTreeRegressionProgram
{
static void Main(string[] args)
{
Console.WriteLine("Decision tree regression C# ");
// 1. load data from file into memory
// 2. create decision tree model
// 3. compute tree model accuracy
// 4. use tree model to make a prediction
Console.WriteLine("End demo ");
Console.ReadLine();
} // Main
} // Program
// --------------------------------------------------------
class DecisionTree
{
public class Node { . . }
public class SplitInfo { . . }
public DecisionTree(int numNodes,
string[] colKind) { . . }
public void BuildTree(double[][] trainX,
double[] trainY) { . . }
private static double[] GetTargets(double[] trainY,
List<int> rows) { . . }
private static double Average(double[] targets) { . . }
private static SplitInfo GetSplitInfo(double[][]
trainX, double[] trainY, List<int> rows,
string[] colKind) { . . }
private static double Variability(double[]
trainY, List<int> rows) { . . }
private static double MeanVariability(double[] trainY,
List<int> rows1, List<int> rows2) { . . }
public void ShowTree() { . . }
public void ShowNode(int nodeID) { . . }
public double Predict(double[] x, bool verbose) { . . }
public double Accuracy(double[][] dataX,
double[] dataY, double pctClose)
}
// --------------------------------------------------------
public class Utils
{
public static double[][] VecToMat(double[] vec,
int rows, int cols) { . . }
public static double[][] MatCreate(int rows,
int cols) { . . }
static int NumNonCommentLines(string fn,
string comment) { . . }
public static double[][] MatLoad(string fn,
int[] usecols, char sep, string comment) { . . }
public static double[] MatToVec(double[][] m) { . . }
public static void MatShow(double[][] m,
int dec, int wid) { . . }
public static void VecShow(int[] vec,
int wid) { . . }
public static void VecShow(double[] vec,
int dec, int wid, bool newLine) { . . }
public static void ListShow(List<int> list,
int wid) { . . }
}
} // ns
Creating the Decision Tree Regression Model
The Main method begins by loading the training data from file into memory:
string trainFile =
"..\\..\\..\\Data\\people_train_tree_10.txt";
// sex, age, State, income, politics
double[][] trainX = Utils.MatLoad(trainFile,
new int[] { 0, 1, 2, 4 }, ',', "#");
double[] trainY =
Utils.MatToVec(Utils.MatLoad(trainFile,
new int[] { 3 }, ',', "#"));
The code assumes that the data file is in a directory named Data in the root project directory. The MatLoad() arguments instruct the method to load columns 0, 1, 2, and 4 as predictors, where lines beginning with "#" are interpreted as comments. The income values in column 3 are loaded into a C# matrix and then converted to an array/vector.
The tiny five-item test data is loaded in the same way:
string testFile =
"..\\..\\..\\Data\\people_test_tree_5.txt";
double[][] testX = Utils.MatLoad(testFile,
new int[] { 0, 1, 2, 4 }, ',', "#");
double[] testY =
Utils.MatToVec(Utils.MatLoad(testFile,
new int[] { 3 }, ',', "#"));
Next, the first three lines of predictor values and the corresponding target income values are displayed:
Console.WriteLine("First three X data: ");
for (int i = 0; i < 3; ++i)
Utils.VecShow(trainX[i], 4, 9, true);
Console.WriteLine("First three target Y : ");
for (int i = 0; i < 3; ++i)
Console.WriteLine(trainY[i].ToString("F4"));
In a non-demo scenario, you'd probably want to display all the training and test data to make sure it has been loaded correctly. Next, the decision tree is created with these four statements:
int treeSize = 7;
// sex, age, State, politics
string[] columnKind = new string[] { "C", "N", "C", "C" };
DecisionTree dt = new DecisionTree(treeSize, columnKind);
dt.BuildTree(trainX, trainY);
The tree size is 2^3 - 1 = 7. In non-demo scenarios, the tree size is the most important parameter to tune. A large enough tree will achieve 100 percent accuracy (assuming no contradictory training data) but will likely overfit and not predict well on new, previously unseen data. A general rule of thumb is to make the tree size roughly one-fourth the number of data items.
The predictor columns are identified as "C" for categorical (sex, State, political leaning) and "N" for numeric (age). Many library decision trees assume that all predictor data is numeric. But if you use categorical data you'll end up with decision rules like, "IF State less-than Nebraska AND . . " which doesn't make much sense.
The tree model is displayed like so:
Console.WriteLine("Tree snapshot: ");
//dt.ShowTree(); // show all nodes in tree
dt.ShowNode(0);
dt.ShowNode(1);
dt.ShowNode(2);
The demo shows just nodes [0], [1], [2], but in a non-demo scenario you'll probably want to see the entire tree using the ShowTree() method.
Evaluating the Decision Tree Model
The demo uses a five-item test dataset that has the same structure as the training data:
1, 0.51, 0, 0.6120, 1
0, 0.55, 0, 0.6270, 0
0, 0.25, 2, 0.2620, 2
0, 0.33, 2, 0.3730, 2
1, 0.29, 1, 0.4620, 0
Because there is no inherent definition of regression model accuracy, it's necessary to implement a program-defined accuracy function. The demo defines a correct prediction as one that is within a specified percentage of the true target income value. The demo uses 10 percent, but the percentage interval to use will vary from problem to problem. The calling statements are:
double trainAcc = dt.Accuracy(trainX, trainY, 0.10);
Console.WriteLine("Train data accuracy = " +
trainAcc.ToString("F4"));
double testAcc = dt.Accuracy(testX, testY, 0.10);
Console.WriteLine("Test data accuracy = " +
testAcc.ToString("F4"));
The demo program scores 0.9000 accuracy on the training data (9 out of 10 correct) but only 0.2000 accuracy on the test data (1 out of 5 correct). This points out one of the biggest weaknesses of decision trees -- they often overfit severely on the training data and predict poorly on new data. That said, every problem scenario is different, and many decision tree models predict very well.
Using the Decision Tree Model
After the decision tree model has been evaluated, the demo concludes by using the model to predict the income of a previously unseen person who is male, age 34, lives in Oklahoma, and is a political moderate:
double[] x = new double[] { 0, 0.34, 2, 1 };
double predY = dt.Predict(x, verbose: true);
// Console.WriteLine("Predicted income = " +
// predY.ToString("F5")); // 0.28600
Console.WriteLine("End demo ");
Console.ReadLine(); // keep shell open
Predictions must be made using the same encoding and normalization that's used when building the tree model. The verbose parameter of the Predict() method displays the logic that's used when computing the prediction. Interpretability is the biggest advantage of using decision tree models. When the verbose parameter equals true, the Predict() method also displays a pseudo-code summary of the prediction rule: "IF (*) AND (column 1 < 0.36) AND (column 0 == 0) THEN Predicted Y = 0.28600." In words, if any, and age is less than 36 and sex equals male, then the predicted income is $28,600."
In a non-demo scenario with a realistic amount of training data, the decision tree prediction rule often repeats variables. For example, you might see something like, "IF column 1 less-than 0.55 AND column 3 not-equal 2 AND column 1 less-than 0.48 AND . . " This wonkiness is characteristic of most decision trees. It is possible to post-process decision tree prediction rules to remove unnecessary duplication of predictor variables, but the demo program, and most machine learning library implementations, do not do so by default.
Wrapping Up
Implementing decision tree regression from scratch is not simple, but by doing so you can modify the system to handle unusual problem scenarios, and you can easily integrate the prediction system into other systems.
The decision tree regression program presented in this article can be used as-is as a template for most regression problems. But you can also modify the demo program in many ways. One common modification is to pass column names to the DecisionTree object so that prediction rule pseudo-code is easier to read, for example, instead of "IF column 1 less-than 0.36 and column 0 is-equal 0 THEN . . " you could emit "IF age less-than 0.36 AND sex is-equal 0 THEN . . "
There are several variations of decision trees that you might consider implementing. A technique called bootstrap aggregation (with the somewhat misleading shortcut name "bagging") creates multiple decision trees where each uses a different randomly selected subset of the rows of the training data, and then the results of the trees are combined to produce a single prediction.
A random forest creates multiple decision trees, each using a different randomly selected subset of predictor variables/columns, and then the results are combined.
In boosted trees ("boosting"), you create a random forest except that each tree is created based on how well the previous tree works. The algorithm is fairly complex. A specific type of boosting is named AdaBoost, and because it's so common, it's pretty much synonymous with "boosting."
Gradient boosting is a generalization of regular boosting. A common, specific type of gradient boosting is named XGBoost ("extreme gradient boosting"). The implementation of XGBoost is very complex -- so much so that only one open source version, developed over the course of several years, is used in practice.