The Data Science Lab
K-Means Data Clustering from Scratch Using C#
K-means is comparatively simple and works well with large datasets, but it assumes clusters are circular/spherical in shape, so it can only find simple cluster geometries.
Data clustering is the process of grouping data items so that similar items are placed in the same cluster. There are several different clustering techniques, and each technique has many variations. Common clustering techniques include k-means, Gaussian mixture model, density-based and spectral. This article explains how to implement one version of k-means clustering from scratch using the C# programming language.
Compared to other clustering techniques, k-means is simple and works well with large datasets. The main weakness of k-means is that it assumes clusters are circular / spherical in shape, and therefore k-means can only find simple cluster geometries.
There are many different versions of k-means clustering but they fall into two general categories. One type of k-means implementation is intended for use in an interactive data science scenario where different values of k (the number of clusters), number of iterations to use, and initialization (Forgy, random partition, k-means++) are applied and then the clustering results are analyzed (typically by eye) to see if any interesting patterns emerge.
The second type of implementation is intended for use as part of a larger system that has a clustering module. This type of k-means implementation is one where the only user-supplied parameter is k and all other parameters have sensible default values. This article presents the second type of implementation.
 [Click on image for larger view.] Figure 1: K-Means Demo Data Before and After Clustering
[Click on image for larger view.] Figure 1: K-Means Demo Data Before and After Clustering
A good way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. For simplicity, the demo uses just N = 18 data items:
0.20, 0.20
0.20, 0.70
0.30, 0.90
. . .
0.80, 0.80
0.50, 0.90
Each data item is a vector with dim = 2 elements. The k-means clustering technique is designed for use with strictly numeric data. After clustering with k = 3, the resulting clustering is: (0, 1, 1, 1, 1, 2, 2, 0, 2, 0, 1, 1, 0, 0, 2, 2, 2, 1). This means data items [0], [7], [9], [12], [13] are assigned to cluster 0, items [1], [2], [3], [4], [10], [11], [17] are assigned to cluster 1, and items [5], [6], [8], [14], [15], [16] are assigned to cluster 2.
Cluster IDs are arbitrary so a clustering of (0, 0, 1, 2) is equivalent to a clustering of (2, 2, 0, 1). Cluster IDs are sometimes called labels.
The data, before and after k-means clustering, is shown in Figure 2. Notice that there is no inherent best clustering of data. The results look reasonable but many other clusterings are possible. The k-means clustering algorithm minimizes a metric called the within-cluster sum of squares, which will be explained shortly.
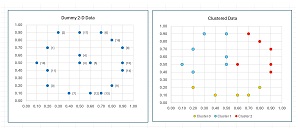 [Click on image for larger view.] Figure 2: K-Means Demo Data Before and After Clustering
[Click on image for larger view.] Figure 2: K-Means Demo Data Before and After Clustering
This article assumes you have intermediate or better programming skill but doesn't assume you know anything about k-means clustering. The demo is implemented using C#, but you should be able to refactor the demo code to another C-family language if you wish.
The source code for the demo program is presented in this article. The complete code is also available in the accompanying file download, and is also available online.
Understanding K-Means Clustering
The k-means clustering algorithm is relatively simple. Expressed in high-level pseudo-code:
assign an initial random clustering
compute means of data items in each cluster
loop until no change in clustering or max iterations
update clustering based on current means
update means based on current clustering
end-loop
return current clustering
There are three main ways to initialize clustering. Forgy initialization picks k data items at random to act as means and then and uses the means to assign the initial clustering. Random partition initialization assigns each data item to a randomly selected cluster ID. The k-means++ initialization scheme is somewhat of a combination of Forgy and random partition. The demo program uses random partition initialization.
The goal of k-means clustering is to find the clustering that minimizes the sum of the squared distances from each data item to its associated cluster mean. For example if a data item is (0.50, 0.80) and it is assigned to cluster [1] and the mean of all the data items assigned to cluster [1] is (0.41, 0.85), then the squared distance between the data item and the mean is (0.50 - 0.41)^2 + (0.80 - 0.85)^2 = 0.0081 + 0.0025 = 0.0106. The sum of all the squared distances for all cluster IDs is called the within-cluster sum of squares (WCSS).
One problem with k-means clustering is that it is an NP-hard problem, which means, loosely speaking, that the only way to guarantee the optimal WCSS clustering is to examine all possible clusterings. This isn't feasible (except for artificially small datasets) because the number of possible clusterings is astronomically large, and so the usual approach is to cluster several times with different initialization and keep track of the best clustering found:
initial cluster data
best wcss = wcss of initial clustering
best clustering = initial clustering
loop n_trials times
curr clustering = cluster the data (with new initialization)
compute wcss of curr clustering
if curr wcss < best wcss
best clustering = curr clustering
best wcss = curr wcss
end-if
end-loop
return best clustering
The only problem with this approach is determining the number of trials to use. One rule of thumb, used by the demo program, is to set the number of trials equal to the number of data items. Because k-means is typically very fast, a larger number of trials can often be used.
When using any clustering algorithm, including k-means, you should normalize the data so that all the columns have roughly the same range, typically between 0 and 1, or between -1 and +1. This prevents a data column with large magnitudes (such as employee incomes like $53,000) from dominating a column with small magnitudes (such as employee years of service like 7) in the distance calculation used in the update-clustering function. The most common types of data normalization are divide-by-k, min-max and z-score.
Overall Program Structure
I used Visual Studio 2022 (Community Free Edition) for the demo program. I created a new C# console application and checked the "Place solution and project in the same directory" option. I specified .NET version 6.0. I named the project ClusterKMeans. I checked the "Do not use top-level statements" option to avoid the program entry point shortcut syntax.
The demo has no significant .NET dependencies and any relatively recent version of Visual Studio with .NET (Core) or the older .NET Framework will work fine. You can also use the Visual Studio Code program if you like.
After the template code loaded into the editor, I right-clicked on file Program.cs in the Solution Explorer window and renamed the file to the slightly more descriptive ClusterKMeansProgram.cs. I allowed Visual Studio to automatically rename class Program.
The overall program structure is presented in Listing 1. All the control logic is in the Main() method. The MatShow(), VecShow() and MatLoad() functions are helpers called by the Main() method..
Listing 1: Overall Program Structure
using System;
using System.IO;
namespace ClusterKMeans
{
internal class ClusterKMeansProgram
{
static void Main(string[] args)
{
Console.WriteLine("Begin C# k-means ");
// load data into X[][]
// show data
// cluster data
// display clustering
Console.WriteLine("End demo ");
Console.ReadLine(); // keep shell open
} // Main
static void MatShow(double[][] m, int dec,
int wid) { . . }
static void VecShow(int[] vec, int wid) { . . }
static double[][] MatLoad(string fn, int[] usecols,
char sep, string comment) { . . }
}
} // Program class
public class KMeans
{
// fields
public double[][] data; // data to cluster
public int k; // number clusters
public int N; // number data items
public int dim; // size each data item
public int trials; // to find best clustering
public int maxIter; // inner update loop
public Random rnd; // for initialization
public int[] clustering;
public double[][] means; // of each cluster
// methods
public KMeans(double[][] data, int k) { . . }
public void Initialize(int seed) { . . }
private void Shuffle(int[] indices) { . . }
private static double SumSquared(double[] v1,
double[] v2) { . . }
private static double Distance(double[] item,
double[] mean) { . . }
private static int ArgMin(double[] v) { . . }
private static bool AreEqual(int[] a1, int[] a2) { . . }
private static int[] Copy(int[] arr) { . . }
public bool UpdateMeans() { . . }
public bool UpdateClustering() { . . }
public int[] ClusterOnce() { . . }
public double WCSS() { . . }
public int[] Cluster() { . . }
} // class KMeans
} // ns
All the clustering logic is in a KMeans class. The ClusterOnce() method computes a clustering of the source data one time using the UpdateMeans() and UpdateClustering() methods. The Cluster() method iteratively calls ClusterOnce() and keeps track of the best clustering found. In addition to the KMeans constructor, the KMeans class has an Initialize() method which is used to reset new clustering parameters on an existing KMeans object.
Loading the Data
The complete demo program is presented in Listing 2. The demo program begins by loading the 18 dummy data items into memory:
double[][] X = new double[18][];
X[0] = new double[] { 0.20, 0.20 };
X[1] = new double[] { 0.20, 0.70 };
X[2] = new double[] { 0.30, 0.90 };
. . .
X[17] = new double[] { 0.50, 0.90 };
For simplicity, the data is hard-coded. In a non-demo scenario, you'll probably want to read the data from a text file into memory using the program-defined MatLoad() helper method like so:
string fn = "..\\..\\..\\Data\\dummy_data_18.txt";
double[][] X = MatLoad(fn, new int[] { 0, 1 },
',', "#");
The data is stored into an array-of-arrays style matrix. The MatLoad() arguments mean to use columns 0 and 1 of the text file, which is comma-delimited, and where the "#" character at the start of a line indicates a comment.
Listing 2: Complete K-Means Program
using System;
using System.IO;
namespace ClusterKMeans
{
internal class ClusterKMeansProgram
{
static void Main(string[] args)
{
Console.WriteLine("\nBegin C# k-means ");
double[][] X = new double[18][];
X[0] = new double[] { 0.20, 0.20 };
X[1] = new double[] { 0.20, 0.70 };
X[2] = new double[] { 0.30, 0.90 };
X[3] = new double[] { 0.50, 0.50 };
X[4] = new double[] { 0.50, 0.60 };
X[5] = new double[] { 0.60, 0.50 };
X[6] = new double[] { 0.70, 0.90 };
X[7] = new double[] { 0.40, 0.10 };
X[8] = new double[] { 0.90, 0.70 };
X[9] = new double[] { 0.80, 0.20 };
X[10] = new double[] { 0.10, 0.50 };
X[11] = new double[] { 0.20, 0.40 };
X[12] = new double[] { 0.60, 0.10 };
X[13] = new double[] { 0.70, 0.10 };
X[14] = new double[] { 0.90, 0.40 };
X[15] = new double[] { 0.90, 0.50 };
X[16] = new double[] { 0.80, 0.80 };
X[17] = new double[] { 0.50, 0.90 };
//string fn = "..\\..\\..\\Data\\dummy_data_18.txt";
//double[][] X = MatLoad(fn, new int[] { 0, 1 },
// ',', "#");
Console.WriteLine("\nData: ");
MatShow(X, 2, 6);
Console.WriteLine("\nClustering with k=3 ");
KMeans km = new KMeans(X, 3);
Console.WriteLine("Done ");
int[] clustering = km.Cluster();
Console.WriteLine("\nclustering = ");
VecShow(clustering, 3);
Console.WriteLine("\nEnd demo ");
Console.ReadLine();
} // Main
// ------------------------------------------------------
static void MatShow(double[][] m, int dec, int wid)
{
for (int i = 0; i < m.Length; ++i)
{
for (int j = 0; j < m[0].Length; ++j)
{
double v = m[i][j];
Console.Write(v.ToString("F" + dec).
PadLeft(wid));
}
Console.WriteLine("");
}
}
// ------------------------------------------------------
static void VecShow(int[] vec, int wid)
{
for (int i = 0; i < vec.Length; ++i)
Console.Write(vec[i].ToString().PadLeft(wid));
Console.WriteLine("");
}
// ------------------------------------------------------
static double[][] MatLoad(string fn, int[] usecols,
char sep, string comment)
{
// self-contained - no dependencies
int nRows = 0;
string line = "";
FileStream ifs = new FileStream(fn, FileMode.Open);
StreamReader sr = new StreamReader(ifs);
while ((line = sr.ReadLine()) != null)
if (line.StartsWith(comment) == false)
++nRows;
sr.Close(); ifs.Close(); // could reset instead
int nCols = usecols.Length;
double[][] result = new double[nRows][];
for (int r = 0; r < nRows; ++r)
result[r] = new double[nCols];
line = "";
string[] tokens = null;
ifs = new FileStream(fn, FileMode.Open);
sr = new StreamReader(ifs);
int i = 0;
while ((line = sr.ReadLine()) != null)
{
if (line.StartsWith(comment) == true)
continue;
tokens = line.Split(sep);
for (int j = 0; j < nCols; ++j)
{
int k = usecols[j]; // into tokens
result[i][j] = double.Parse(tokens[k]);
}
++i;
}
sr.Close(); ifs.Close();
return result;
}
// ------------------------------------------------------
} // Program
public class KMeans
{
public double[][] data;
public int k;
public int N;
public int dim;
public int trials; // to find best
public int maxIter; // inner loop
public Random rnd;
public int[] clustering;
public double[][] means;
public KMeans(double[][] data, int k)
{
this.data = data; // by ref
this.k = k;
this.N = data.Length;
this.dim = data[0].Length;
this.trials = N; // for Cluster()
this.maxIter = N * 2; // for ClusterOnce()
this.Initialize(0); // seed, means, clustering
}
public void Initialize(int seed)
{
this.rnd = new Random(seed);
this.clustering = new int[this.N];
this.means = new double[this.k][];
for (int i = 0; i < this.k; ++i)
this.means[i] = new double[this.dim];
// Random Partition (not Forgy)
int[] indices = new int[this.N];
for (int i = 0; i < this.N; ++i)
indices[i] = i;
Shuffle(indices);
for (int i = 0; i < this.k; ++i) // first k items
this.clustering[indices[i]] = i;
for (int i = this.k; i < this.N; ++i)
this.clustering[indices[i]] =
this.rnd.Next(0, this.k); // remaining items
// VecShow(this.clustering, 4);
this.UpdateMeans();
}
private void Shuffle(int[] indices)
{
int n = indices.Length;
for (int i = 0; i < n; ++i)
{
int r = this.rnd.Next(i, n);
int tmp = indices[i];
indices[i] = indices[r];
indices[r] = tmp;
}
}
private static double SumSquared(double[] v1,
double[] v2)
{
int dim = v1.Length;
double sum = 0.0;
for (int i = 0; i < dim; ++i)
sum += (v1[i] - v2[i]) * (v1[i] - v2[i]);
return sum;
}
private static double Distance(double[] item,
double[] mean)
{
double ss = SumSquared(item, mean);
return Math.Sqrt(ss);
}
private static int ArgMin(double[] v)
{
int dim = v.Length;
int minIdx = 0;
double minVal = v[0];
for (int i = 0; i < v.Length; ++i)
{
if (v[i] < minVal)
{
minVal = v[i];
minIdx = i;
}
}
return minIdx;
}
private static bool AreEqual(int[] a1, int[] a2)
{
int dim = a1.Length;
for (int i = 0; i < dim; ++i)
if (a1[i] != a2[i]) return false;
return true;
}
private static int[] Copy(int[] arr)
{
int dim = arr.Length;
int[] result = new int[dim];
for (int i = 0; i < dim; ++i)
result[i] = arr[i];
return result;
}
public bool UpdateMeans()
{
// verify no zero-counts
int[] counts = new int[this.k];
for (int i = 0; i < this.N; ++i)
{
int cid = this.clustering[i];
++counts[cid];
}
for (int kk = 0; kk < this.k; ++kk)
{
if (counts[kk] == 0)
throw
new Exception("0-count in UpdateMeans()");
}
// compute proposed new means
for (int kk = 0; kk < this.k; ++kk)
counts[kk] = 0; // reset
double[][] newMeans = new double[this.k][];
for (int i = 0; i < this.k; ++i)
newMeans[i] = new double[this.dim];
for (int i = 0; i < this.N; ++i)
{
int cid = this.clustering[i];
++counts[cid];
for (int j = 0; j < this.dim; ++j)
newMeans[cid][j] += this.data[i][j];
}
for (int kk = 0; kk < this.k; ++kk)
if (counts[kk] == 0)
return false; // bad attempt to update
for (int kk = 0; kk < this.k; ++kk)
for (int j = 0; j < this.dim; ++j)
newMeans[kk][j] /= counts[kk];
// copy new means
for (int kk = 0; kk < this.k; ++kk)
for (int j = 0; j < this.dim; ++j)
this.means[kk][j] = newMeans[kk][j];
return true;
} // UpdateMeans()
public bool UpdateClustering()
{
// verify no zero-counts
int[] counts = new int[this.k];
for (int i = 0; i < this.N; ++i)
{
int cid = this.clustering[i];
++counts[cid];
}
for (int kk = 0; kk < this.k; ++kk)
{
if (counts[kk] == 0)
throw new
Exception("0-count in UpdateClustering()");
}
// proposed new clustering
int[] newClustering = new int[this.N];
for (int i = 0; i < this.N; ++i)
newClustering[i] = this.clustering[i];
double[] distances = new double[this.k];
for (int i = 0; i < this.N; ++i)
{
for (int kk = 0; kk < this.k; ++kk)
{
distances[kk] =
Distance(this.data[i], this.means[kk]);
int newID = ArgMin(distances);
newClustering[i] = newID;
}
}
if (AreEqual(this.clustering, newClustering) == true)
return false; // no change; short-circuit
// make sure no count went to 0
for (int i = 0; i < this.k; ++i)
counts[i] = 0; // reset
for (int i = 0; i < this.N; ++i)
{
int cid = newClustering[i];
++counts[cid];
}
for (int kk = 0; kk < this.k; ++kk)
if (counts[kk] == 0)
return false; // bad update attempt
// no 0 counts so update
for (int i = 0; i < this.N; ++i)
this.clustering[i] = newClustering[i];
return true;
} // UpdateClustering()
public int[] ClusterOnce()
{
bool ok = true;
int sanityCt = 1;
while (sanityCt <= this.maxIter)
{
if ((ok = this.UpdateClustering() == false)) break;
if ((ok = this.UpdateMeans() == false)) break;
++sanityCt;
}
return this.clustering;
} // ClusterOnce()
public double WCSS()
{
// within-cluster sum of squares
double sum = 0.0;
for (int i = 0; i < this.N; ++i)
{
int cid = this.clustering[i];
double[] mean = this.means[cid];
double ss = SumSquared(this.data[i], mean);
sum += ss;
}
return sum;
}
public int[] Cluster()
{
double bestWCSS = this.WCSS(); // initial clustering
int[] bestClustering = Copy(this.clustering);
for (int i = 0; i < this.trials; ++i)
{
this.Initialize(i); // new seed, means, clustering
int[] clustering = this.ClusterOnce();
double wcss = this.WCSS();
if (wcss < bestWCSS)
{
bestWCSS = wcss;
bestClustering = Copy(clustering);
}
}
return bestClustering;
} // Cluster()
} // class KMeans
} // ns
The demo program displays the loaded data using the MatShow() function:
Console.WriteLine("Data: ");
MatShow(X, 2, 6); // 2 decimals, 6 wide
In a non-demo scenario, you might want to display all the data to make sure it was loaded properly.
Clustering the Data
The KMeans clustering object is created and used like so:
Console.WriteLine("Clustering with k=3 ");
KMeans km = new KMeans(X, 3);
Console.WriteLine("Done ");
int[] clustering = km.Cluster();
The number of clusters, k, must be supplied. There is no good way to programmatically determine an optimal number of clusters. A somewhat subjective approach for determining a good number of clusters is called the elbow technique. You try different values of k and plot the associated WCSS values. When the WCSS value doesn't change much at some point, the associated value of k is a good candidate. See the article, "Determining the Number of Clusters Using the Elbow and the Knee Techniques."
The demo concludes by displaying the clustering results:
Console.WriteLine("clustering = ");
VecShow(clustering, 3);
The results look like:
1 1 2 0 0 1 . . .
The clustering information can be displayed in several ways. For example, instead of displaying by data item, you can display by cluster ID. Or, you can display each data item and its associated cluster ID on the same line.
Wrapping Up
The k-means implementation presented in this article can be used as-is or modified in several ways. The demo uses random partition initialization. The order of the N data items is randomized, then the first k data items are assigned to the first k cluster IDS, and then the remaining N-k data items are assigned to a random cluster ID. This approach guarantees that there is at least one data item assigned to each cluster ID but doesn't guarantee that the initial distribution of cluster ID counts are equal. Instead of assigning random cluster IDs, you can cycle though the cluster IDs sequentially.
The Cluster() method calls ClusterOnce() this.trials times looking for the clustering that has the smallest within-cluster sum of squares. Instead of iterating a fixed number of times, you can track previous-wcss and current-wcss and exit the loop when the two values do not change after a threshold value (such as N times).
The demo implementation assumes the source data is normalized. An alternative is to integrate the data normalization into the k-means system.
The UpdateClustering() uses Euclidean distance to assign each data item to the cluster ID that has the closest mean. There are alternatives to Euclidean distance, such as Manhattan distance and Minkowski distance. However, Euclidean distance works fine in most scenarios.