In-Depth
Improved Permutations with the BigInteger Data Type
The major challenge when working with permutations is that the factorial function gets very, very large very, very quickly. The BigInteger data type was introduced in the .NET Framework 4.0; it enables the writing of effective permutation code.
A permutation of n items is a rearrangement of those n items. For example, if n = 3 and the three items are the names "Adam", "Barb", and "Carl", one permutation of the items is "Carl", "Adam", "Barb". More generally, a mathematical permutation of order n is a rearrangement of the integers 0 through n-1: for example, (2,0,1). Permutations are fundamentally important in computer science.
The number of possible permutations for order n is factorial(n), often abbreviated as n! in math literature. Factorial(n) is defined as n * (n-1) * (n-2) * . . . * 1. For example, if n = 3, there are n! = 3 * 2 * 1 = 6 possible permutation elements: (0,1,2), (0,2,1), (1,0,2), (1,2,0), (2,0,1), (2,1,0). The major challenge when working with permutations is that the factorial function gets very, very large very, very quickly. For example, 30! = 265,252,859,812,191,058,636,308,480,000,000 which is vastly larger than the estimated age of the universe in seconds.
The BigInteger data type was introduced in the .NET Framework 4.0 and enables the writing of effective permutation code. The BigInteger data type can handle arbitrarily large integer values; the screenshot in Figure 1 gives you an idea of where I'm headed.
The first part of the screenshot indicates that the demo program has the ability to create a mathematical permutation object with a given order, and generate and display all permutation elements. Behind the scenes, the demo is calling a permutation successor method.
The second part of the demo program illustrates applying mathematical permutations to a string array. The next part of the demo shows the ability to compute arbitrarily large factorial values. And the final part of the screenshot indicates that the demo program can jump directly to a specified permutation element -- a surprisingly difficult task.
Mathematical permutations are closely related to, and sometimes confused with, mathematical combinations. A mathematical combination of order n is a subset of the values 0 to n-1, where the order of the values in the subset doesn't matter. For example, if n = 5, then the first six combination elements for subset size k = 2 are (0,1), (0,2), (0,3), (0,4), (1,2), (1,3) and so on. I discussed combinations in "Improved Combinations with the BigInteger Data Type" here.
Overall Program Structure
The program that generated the screenshot in
Figure 1 is a single C# console application. The program structure is presented in
Listing 1. I used VS 2010, but any version of VS that supports the .NET Framework 4 will work. I named my project ImprovedPermutations, then renamed the VS template-generated Program.cs file to PermutationsProgram.cs, which automatically renamed class Program. I commented out the template-generated using statements except for the reference to the System namespace, then added a reference to the System.Numerics namespace that houses the BigInteger data type.
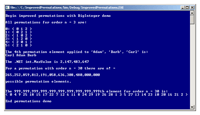
[Click on image for larger view.] |
| Figure 1. Mathematical permutations with the BigInteger data type. |
For simplicity, I placed the Permutation class definition in the same source file as the console application. The Permutation class has two member fields, the order n, and an array named data to hold the permutation values (sometimes called atoms.)
The Permutation constructor creates the so-called identity permutation element, which is 0 through n-1. In order to keep the size of my demo code small, I removed most normal error-checking, such as verifying that the order parameter n is positive.
The overloaded ToString method returns a string of the values in data, separated by blank spaces and enclosed with parentheses. If you intend to display many Permutation objects, you might want to consider using the StringBuilder class instead of using string concatenation.
The Successor Method
The method to generate the successor to a Permutation object is given in
Listing 2.
The most usual way to define permutation sequencing is called lexicographical order. This means that if permutation elements are interpreted as ordinary integers, the elements are listed from smallest to largest. For example, if n = 3, then lexicographical order is 012, 021, 102, 120, 201, 210 (twelve, twenty-one, etc.)
One design decision to make with the Successor method is to determine what to return as the successor of the last element. Notice that the last element in lexicographical order is the one element that has n-1 at data[0], and also 0 at data[n-1]. In Listing 2, I decide to return null. Alternatives are to return the first element or throw an exception.
With a Permutation constructor, Successor and ToString methods, all permutation elements can be displayed like so:
int n = 3;
Permutation p1 = new Permutation(n);
Console.WriteLine("All permutations for order n = 3 are:\n");
int ct = 0;
while (p1 != null)
{
Console.WriteLine(ct + ": " + p1.ToString());
p1 = p1.Successor();
++ct;
}
The Factorial Function
Before the arrival of the BigInteger data type, coding a factorial function that could handle input arguments larger than 20 was very difficult. The BigInteger type makes things easy:
public static BigInteger Factorial(int k)
{
if (k == 0) return 1;
BigInteger ans = 1;
for (int i = 1; i <= k; ++i)
ans *= i;
return ans;
}
I define the Factorial function using the static modifier because the function is not tied to a particular Permutation object. I use k as the input parameter name, instead of the more common n, to avoid confusion with the n Permutation member. Both Factorial(0) and Factorial(1) are 1 by definition.
The demo program calls the Factorial function like so:
n = 30;
BigInteger nFactorial = Permutation.Factorial(n);
Console.WriteLine("The .NET int.MaxValue is " +
int.MaxValue.ToString("#,###"));
Console.WriteLine("For a permutation with order n = 30 there are n! = \n");
Console.WriteLine(nFactorial.ToString("#,###"));
Console.WriteLine("possible permutation elements.");
Applying a Permutation to a String Array
Many systems-programming scenarios use mathematical permutations. But in many application-programming scenarios, you may be more interested in rearrangements of strings or other objects. One way to think about a mathematical permutation is that it's a mapping of the numbers 0 trough n-1. Because .NET arrays are indexed from 0 to array length-1, applying a Permutation object to an array of strings (or any other object) is quite easy. One way to do this is to write an ApplyTo method:
public string[] ApplyTo(string[] arr)
{
string[] result = new string[n];
for (int i = 0; i < n; ++i)
result[i] = arr[data[i]];
return result;
}
Now, suppose you have three strings:
string[] names = new string[] { "Adam", "Barb", "Carl" };
And suppose you want to apply to 4th permutation element -- (2,0,1) -- to the array. This should result in name[2] going to [0], name[0] going to [1], and name[1] going to [2]. One crude way to do this:
Permutation p2 = new Permutation(3); // 0th
p2 = p2.Successor(); // 1
p2 = p2.Successor(); // 2
p2 = p2.Successor(); // 3
p2 = p2.Successor(); // 4
names = p2.ApplyTo(names);
Console.WriteLine("The 4th permutation element applied to Adam" +
" Barb Carl is:");
for (int i = 0; i < names.Length; ++i)
Console.Write(names[i] + " ");
Although this technique works, you wouldn't want to use it for large values of k.
The Kth Lexicographical Element
In some situations, you may want to generate a specific permutation element. For example, if n = 3, you might want the 4th element, (2,0,1). At first thought this would seem to be an easy problem with an easy solution: just create the identity permutation and then iterate k times, calling the successor method. However, because the number of permutation elements can be enormous, with even moderately large values of k the approach would just take too long. But if you have an Element method, you could write code like:
Permutation p = new Permutation(3);
p = p.Element(4);
So, an important permutation function is one that directly returns the kth lexicographical element. This is a fascinating problem, and one that has a beautiful solution using something called the factoradic of a number. It turns out that every integer can be uniquely expressed using factorials. For example, the number 1,047 can be expressed as (1 * 6!) + (2 * 5!) + (3 * 4!) + (2 * 3!) + (1 * 2!) + (1 * 1!) = 720 + 240 + 72 + 12 + 2 + 1. So, the factoradic of 1,047 is (1,2,3,2,1,1). And it turns out that the factoradic of a number k can be directly converted to the kth permutation. The code for the Element method is given in Listing 3.
The code for the Element method is rather tricky, but it's unlikely you'll ever need to modify the code. I present a detailed explanation of how to convert a factoradic to a permutation in "Using Permutations in .NET for Improved Systems Security", available at the MSDN Library.
The demo program calls the Element method like so:
Permutation p3 = new Permutation(n);
BigInteger k = BigInteger.Parse("999999999999999999999999999999");
p3 = p3.Element(k);
Console.WriteLine("The " + k.ToString("#,###") + "th element " +
" for order n = 30 is:");
Console.WriteLine(p3.ToString());
The entire code file can be seen in Listing 4.
BigInteger = BigSolutions
Before the introduction of the BigInteger data type, working with permutations was extremely difficult. You either had to limit yourself to very small values of the order n (typically 20 or less), or essentially create a custom class that had the ability to represent and manipulate arbitrarily large integer values. The BigInteger data type removes that obstacle and makes working with permutations dramatically easier.
About the Author
Dr. James McCaffrey works for Microsoft Research in Redmond, Wash. He has worked on several Microsoft products including Azure and Bing. James can be reached at [email protected].