Neural Network Lab
Neural Network Activation Functions in C#
James McCaffrey explains what neural network activation functions are and why they're necessary, and explores three common activation functions.
Understanding neural network activation functions is essential whether you use an existing software tool to perform neural network analysis of data or write custom neural network code. This article describes what neural network activation functions are, explains why activation functions are necessary, describes three common activation functions, gives guidance on when to use a particular activation function, and presents C# implementation details of common activation functions.
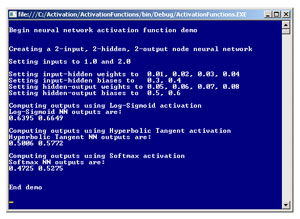
The best way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. The demo program creates a fully connected, two-input, two-hidden, two-output node neural network. After setting the inputs to 1.0 and 2.0 and setting arbitrary values for the 10 input-to-hidden and hidden-to-output weights and biases, the demo program computes and displays the two output values using three different activation functions.
 [Click on image for larger view.]
Figure 1. The activation function demo.
[Click on image for larger view.]
Figure 1. The activation function demo.
The demo program illustrates three common neural network activation functions: logistic sigmoid, hyperbolic tangent and softmax. Using the logistic sigmoid activation function for both the input-hidden and hidden-output layers, the output values are 0.6395 and 0.6649. The same inputs, weights and bias values yield outputs of 0.5006 and 0.5772 when the hyperbolic tangent activation function is used. And the outputs when using the softmax activation function are 0.4725 and 0.5275.
This article assumes you have at least intermediate-level programming skills and a basic knowledge of the neural network feed-forward mechanism. The demo program is coded in C#, but you shouldn't have too much trouble refactoring the code to another language if you wish. To keep the main ideas clear, all normal error checking has been removed.
The Demo Program
The entire demo program, with a few minor edits, is presented in Listing 1. To create the demo, I launched Visual Studio (any recent version will work) and created a new C# console application program named ActivationFunctions. After the template code loaded, I removed all using statements except the one that references the System namespace. In the Solution Explorer window I renamed the file Program.cs to ActivationProgram.cs, and Visual Studio automatically renamed the class Program.
Listing 1. Activation demo program structure.
using System;
namespace ActivationFunctions
{
class ActivationProgram
{
static void Main(string[] args)
{
try
{
Console.WriteLine("Begin neural network activation function demo");
Console.WriteLine("Creating a 2-input, 2-hidden, 2-output node neural network");
DummyNeuralNetwork dnn = new DummyNeuralNetwork();
Console.WriteLine("Setting inputs to 1.0 and 2.0");
double[] inputs = new double[] { 1.0, 2.0 };
dnn.SetInputs(inputs);
Console.WriteLine("Setting input-hidden weights to 0.01, 0.02, 0.03, 0.04");
Console.WriteLine("Setting input-hidden biases to 0.3, 0.4");
Console.WriteLine("Setting hidden-output weights to 0.05, 0.06, 0.07, 0.08");
Console.WriteLine("Setting hidden-output biases to 0.5, 0.6");
double[] weights = new double[] {0.01, 0.02, 0.03, 0.04,
0.3, 0.4,
0.05, 0.06, 0.07, 0.08,
0.5, 0.6 };
dnn.SetWeights(weights);
Console.WriteLine("Computing outputs using Log-Sigmoid activation");
dnn.ComputeOutputs("logsigmoid");
Console.WriteLine("Log-Sigmoid NN outputs are: ");
Console.Write(dnn.outputs[0].ToString("F4") + " ");
Console.WriteLine(dnn.outputs[1].ToString("F4"));
Console.WriteLine("Computing outputs using Hyperbolic Tangent activation");
dnn.ComputeOutputs("hyperbolictangent");
Console.WriteLine("Hyperbolic Tangent NN outputs are: ");
Console.Write(dnn.outputs[0].ToString("F4") + " ");
Console.WriteLine(dnn.outputs[1].ToString("F4"));
Console.WriteLine("Computing outputs using Softmax activation");
dnn.ComputeOutputs("softmax");
Console.WriteLine("Softmax NN outputs are: ");
Console.Write(dnn.outputs[0].ToString("F4") + " ");
Console.WriteLine(dnn.outputs[1].ToString("F4"));
Console.WriteLine("End demo");
Console.ReadLine();
}
catch (Exception ex)
{
Console.WriteLine(ex.Message);
Console.ReadLine();
}
} // Main
} // Program
public class DummyNeuralNetwork
{
public double[] inputs;
public double ihWeight00;
public double ihWeight01;
public double ihWeight10;
public double ihWeight11;
public double ihBias0;
public double ihBias1;
public double ihSum0;
public double ihSum1;
public double ihResult0;
public double ihResult1;
public double hoWeight00;
public double hoWeight01;
public double hoWeight10;
public double hoWeight11;
public double hoBias0;
public double hoBias1;
public double hoSum0;
public double hoSum1;
public double hoResult0;
public double hoResult1;
public double[] outputs;
public DummyNeuralNetwork()
{
this.inputs = new double[2];
this.outputs = new double[2];
}
public void SetInputs(double[] inputs)
{
inputs.CopyTo(this.inputs, 0);
}
public void SetWeights(double[] weightsAndBiases)
{
int k = 0;
ihWeight00 = weightsAndBiases[k++];
ihWeight01 = weightsAndBiases[k++];
ihWeight10 = weightsAndBiases[k++];
ihWeight11 = weightsAndBiases[k++];
ihBias0 = weightsAndBiases[k++];
ihBias1 = weightsAndBiases[k++];
hoWeight00 = weightsAndBiases[k++];
hoWeight01 = weightsAndBiases[k++];
hoWeight10 = weightsAndBiases[k++];
hoWeight11 = weightsAndBiases[k++];
hoBias0 = weightsAndBiases[k++];
hoBias1 = weightsAndBiases[k++];
}
public void ComputeOutputs(string activationType)
{
// Assumes this.inputs[] have values
ihSum0 = (inputs[0] * ihWeight00) + (inputs[1] * ihWeight10);
ihSum0 += ihBias0;
ihSum1 = (inputs[0] * ihWeight01) + (inputs[1] * ihWeight11);
ihSum1 += ihBias1;
ihResult0 = Activation(ihSum0, activationType, "ih");
ihResult1 = Activation(ihSum1, activationType, "ih");
hoSum0 = (ihResult0 * hoWeight00) + (ihResult1 * hoWeight10);
hoSum0 += hoBias0;
hoSum1 = (ihResult0 * hoWeight01) + (ihResult1 * hoWeight11);
hoSum1 += hoBias1;
hoResult0 = Activation(hoSum0, activationType, "ho");
hoResult1 = Activation(hoSum1, activationType, "ho");
outputs[0] = hoResult0;
outputs[1] = hoResult1;
}
public double Activation(double x, string activationType, string layer)
{
if (activationType == "logsigmoid")
return LogSigmoid(x);
else if (activationType == "hyperbolictangent")
return HyperbolicTangtent(x);
else if (activationType == "softmax")
return SoftMax(x, layer);
else
throw new Exception("Not implemented");
}
public double LogSigmoid(double x)
{
if (x < -45.0) return 0.0;
else if (x > 45.0) return 1.0;
else return 1.0 / (1.0 + Math.Exp(-x));
}
public double HyperbolicTangtent(double x)
{
if (x < -45.0) return -1.0;
else if (x > 45.0) return 1.0;
else return Math.Tanh(x);
}
public double SoftMax(double x, string layer)
{
// Determine max
double max = double.MinValue;
if (layer == "ih")
max = (ihSum0 > ihSum1) ? ihSum0 : ihSum1;
else if (layer == "ho")
max = (hoSum0 > hoSum1) ? hoSum0 : hoSum1;
// Compute scale
double scale = 0.0;
if (layer == "ih")
scale = Math.Exp(ihSum0 - max) + Math.Exp(ihSum1 - max);
else if (layer == "ho")
scale = Math.Exp(hoSum0 - max ) + Math.Exp(hoSum1 - max);
return Math.Exp(x - max) / scale;
}
}
} // ns
The neural network is defined in the DummyNeuralNetwork class. You should be able to determine the meaning of the weight and bias class members. For example, class member ihWeights01 holds the weight value for input node 0 to hidden node 1. Member hoWeights10 holds the weight for hidden node 1 to output node 0.
Member ihSum0 is the sum of the products of inputs and weights, plus the bias value, for hidden node 0, before an activation function has been applied. Member ihResult0 is the value emitted from hidden node 0 after an activation function has been applied to ihSum0.
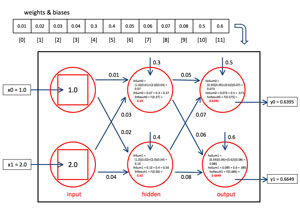
The computations for the outputs when using the logistic sigmoid activation function are shown in Figure 2. For hidden node 0, the top-most hidden node in the figure, the sum is (1.0)(0.01) + (2.0)(0.03) + 0.3 = 0.37. Notice that I use separate bias values rather than the annoying (to me, anyway) technique of treating bias values as special weights associated with a dummy 1.0 input value. The activation function is indicated by F in the figure. After applying the logistic sigmoid function to 0.37, the result is 0.59. This value is used as input to the output-layer nodes.
 [Click on image for larger view.]
Figure 2. Logistic sigmoid activation output computations.
[Click on image for larger view.]
Figure 2. Logistic sigmoid activation output computations.
The Logistic Sigmoid Activation Function
In neural network literature, the most common activation function discussed is the logistic sigmoid function. The function is also called log-sigmoid, or just plain sigmoid. The function is defined as:
f(x) = 1.0 / (1.0 + e-x)
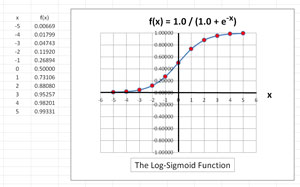
The graph of the log-sigmoid function is shown in Figure 3. The log-sigmoid function accepts any x value and returns a value between 0 and 1. Values of x smaller than about -10 return a value very, very close to 0.0. Values of x greater than about 10 return a value very, very close to 1.
 [Click on image for larger view.]
Figure 3. The logistic sigmoid function.
[Click on image for larger view.]
Figure 3. The logistic sigmoid function.
Because the log-sigmoid function constrains results to the range (0,1), the function is sometimes said to be a squashing function in neural network literature. It is the non-linear characteristics of the log-sigmoid function (and other similar activation functions) that allow neural networks to model complex data.
The demo program implements the log-sigmoid function as:
public double LogSigmoid(double x)
{
if (x < -45.0) return 0.0;
else if (x > 45.0) return 1.0;
else return 1.0 / (1.0 + Math.Exp(-x));
}
In the early days of computing, arithmetic overflow and underflow were not always handled well by compilers, so input parameter checks like x < -45.0 were often used. Although compilers are now much more robust, it's somewhat traditional to include such boundary checks in neural network activation functions.
The Hyperbolic Tangent Activation Function
The hyperbolic tangent function is a close cousin to the log-sigmoid function. The hyperbolic tangent function is defined as:
f(x) = (ex - e-x) / (ex + e-x)
The hyperbolic tangent function is often abbreviated as tanh. When graphed, the hyperbolic tangent function looks very similar to the log-sigmoid function. The important difference is that tanh returns a value between -1 and +1 instead of between 0 and 1.
Most modern programming languages, including C#, have a built-in hyperbolic tangent function defined. The demo program implements the hyperbolic tangent activation function as:
public double HyperbolicTangtent(double x)
{
if (x < -45.0) return -1.0;
else if (x > 45.0) return 1.0;
else return Math.Tanh(x);
}
The Softmax Activation Function
The softmax activation function is designed so that a return value is in the range (0,1) and the sum of all return values for a particular layer is 1.0. For example, the demo program output values when using the softmax activation function are 0.4725 and 0.5275 -- notice they sum to 1.0. The idea is that output values can then be loosely interpreted as probability values, which is extremely useful when dealing with categorical data.
The softmax activation function is best explained by example. Consider the demo shown in Figure 1 and Figure 2. The pre-activation sums for the hidden layer nodes are 0.37 and 0.50. First, a scaling factor is computed:
Scale = Exp(0.37) + Exp(0.50) = 1.4477 + 1.6487 = 3.0965
Then the activation return values are computed like so:
F(0.37) = Exp(0.37) / scale = 1.4477 / 3.0965 = 0.47
F(0.50) = Exp(0.50) / scale = 1.6487 / 3.0965 = 0.53
Notice that unlike the log-sigmoid and tanh activation functions, the softmax function needs all the pre-activation sums for a particular layer. A naive implementation of the softmax activation function could be:
public double SoftMax(double x, string layer)
{
// Naive version
double scale = 0.0;
if (layer == "ih")
scale = Math.Exp(ihSum0) + Math.Exp(ihSum1);
else if (layer == "ho")
scale = Math.Exp(hoSum0) + Math.Exp(hoSum1);
else
throw new Exception("Unknown layer");
return Math.Exp(x) / scale;
}
The demo program uses a more sophisticated implementation that relies on properties of the exponential function, as shown in Listing 2.
Listing 2. Implementation relying on properties of the exponential function.
public double SoftMax(double x, string layer)
{
double max = double.MinValue;
if (layer == "ih")
max = (ihSum0 > ihSum1) ? ihSum0 : ihSum1;
else if (layer == "ho")
max = (hoSum0 > hoSum1) ? hoSum0 : hoSum1;
double scale = 0.0;
if (layer == "ih")
scale = Math.Exp(ihSum0 - max) + Math.Exp(ihSum1 - max);
else if (layer == "ho")
scale = Math.Exp(hoSum0 - max ) + Math.Exp(hoSum1 - max);
return Math.Exp(x - max) / scale;
}
The algebra is a bit tricky, but the main idea is to avoid arithmetic overflow. If you trace through the function, and use the fact that Exp(a - b) = Exp(a) / Exp(b), you'll see how the logic works.
Which Activation Functions Should You Use?
There are a few guidelines for choosing neural network activation functions. If all input and output data is numeric, and none of the values are negative, the log-sigmoid function is a good option. For numeric input and output where values can be either positive or negative, the hyperbolic tangent function is often a good choice. In situations where input is numeric and the output is categorical, such as a stock recommendation to sell, buy or hold, using softmax activation for the output layer and the tanh function for the hidden layer often works well. Data analysis with neural networks often involves quite a bit of trial and error, including experimenting with different combinations of activation functions.
There are many other activation functions in addition to the ones described in this article. The Heaviside step function can be defined as:
public double Step(double x)
{
if (x < 0.0) return 0.0;
else return 1.0;
}
This function does not have the non-linear characteristics of the functions described in this article. In my experience, the step function rarely performs well except in some rare cases with (0,1)-encoded binary data.
Another activation function you might come across is the Gaussian function. The function is also called the "normal distribution." When graphed it has a bell-shaped curve. Small and large values of x return 0.0 and middle-range values of x return a value between 0 and 1. The Gaussian function is typically used with a special type of neural network called a Radial Basis Function (RBF) network.