In-Depth
K-Means Data Clustering Using C#
Learn how to cluster your numeric data using the k-means algorithm in this step-by-step guide.
Data clustering is the process of placing data items into groups so that items within a group are similar and items in different groups are dissimilar. The most common technique for clustering numeric data is called the k-means algorithm.
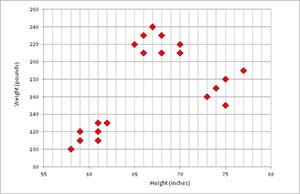
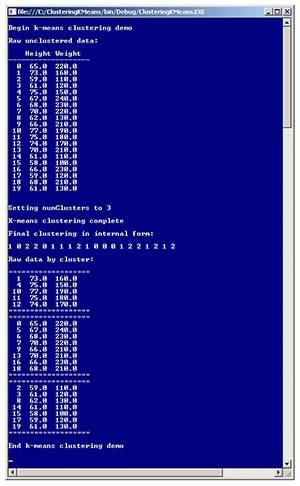
Take a look at the data and graph in Figure 1. Each data tuple has two dimensions: a person's height (in inches) and weight (in pounds). The data was artificially constructed so that there are clearly three distinct clusters. The screenshot in Figure 2 shows a demo C# program that uses the k-means algorithm to cluster the data.
 [Click on image for larger view.]
Figure 1. Raw Data to Cluster
[Click on image for larger view.]
Figure 1. Raw Data to Cluster
 [Click on image for larger view.]
Figure 2. K-Means Clustering Demo
[Click on image for larger view.]
Figure 2. K-Means Clustering Demo
There are many different clustering algorithms. The k-means algorithm is applicable only for purely numeric data. Data clustering is used as part of several machine-learning algorithms, and data clustering can also be used to perform ad hoc data analysis. I consider the k-means algorithm to be one of three "Hello Worlds" of machine learning (along with logistic regression and naive Bayes classification).
The K-Means Algorithm
The k-means algorithm, sometimes called Lloyd's algorithm, is simple and elegant. The algorithm is illustrated in Figures 3-7. In pseudo-code, k-means is:
initialize clustering
loop until done
compute mean of each cluster
update clustering based on new means
end loop
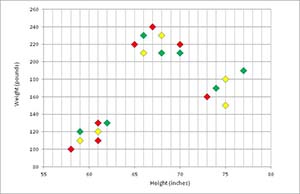
Figure 3 represents an initial clustering of data. Visually, each data point is colored red, yellow or green to indicate cluster membership.
 [Click on image for larger view.]
Figure 3. Initial Random Clustering
[Click on image for larger view.]
Figure 3. Initial Random Clustering
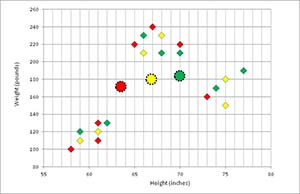
In Figure 4, the means of each of the three clusters have been computed, and these means are indicated by the three colored circles.
 [Click on image for larger view.]
Figure 4. Initial Cluster Means
[Click on image for larger view.]
Figure 4. Initial Cluster Means
In Figure 5, each data tuple is examined and assigned to the closest cluster represented by its associated mean.
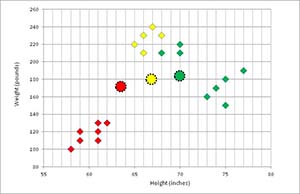 [Click on image for larger view.]
Figure 5. Clustering Updated
[Click on image for larger view.]
Figure 5. Clustering Updated
In Figure 6, the new cluster means have been computed.
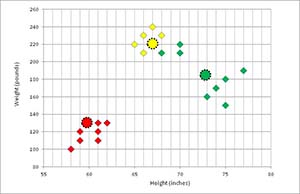 [Click on image for larger view.]
Figure 6. New Means Computed
[Click on image for larger view.]
Figure 6. New Means Computed
In Figure 7, the clustering is updated. You can see that the clustering has stabilized. The k-means algorithm does not guarantee an optimal solution. However, the algorithm typically converges to a solution very quickly.
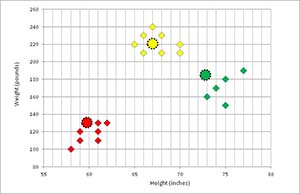 [Click on image for larger view.]
Figure 7. Final Clustering Update
[Click on image for larger view.]
Figure 7. Final Clustering Update
Overall Program Structure
The overall structure of the demo program, with some minor edits to save space, is presented in Listing 1. To create the demo program, I launched Visual Studio and created a C# console application named ClusteringKMeans. The demo has no significant .NET dependencies, and any version of Visual Studio will work. After the template code loaded, I deleted all references to namespaces except the reference to the top-level System namespace. In the Solution Explorer window, I renamed file Program.cs to the more descriptive KMeansDemo.cs and Visual Studio automatically renamed class Program for me.
Listing 1: K-Means Demo Program Structure
using System;
namespace ClusteringKMeans
{
class KMeansDemo
{
static void Main(string[] args)
{
Console.WriteLine("Begin k-means demo");
double[][] rawData = new double[20][];
rawData[0] = new double[] { 65.0, 220.0 };
rawData[1] = new double[] { 73.0, 160.0 };
rawData[2] = new double[] { 59.0, 110.0 };
rawData[3] = new double[] { 61.0, 120.0 };
rawData[4] = new double[] { 75.0, 150.0 };
rawData[5] = new double[] { 67.0, 240.0 };
rawData[6] = new double[] { 68.0, 230.0 };
rawData[7] = new double[] { 70.0, 220.0 };
rawData[8] = new double[] { 62.0, 130.0 };
rawData[9] = new double[] { 66.0, 210.0 };
rawData[10] = new double[] { 77.0, 190.0 };
rawData[11] = new double[] { 75.0, 180.0 };
rawData[12] = new double[] { 74.0, 170.0 };
rawData[13] = new double[] { 70.0, 210.0 };
rawData[14] = new double[] { 61.0, 110.0 };
rawData[15] = new double[] { 58.0, 100.0 };
rawData[16] = new double[] { 66.0, 230.0 };
rawData[17] = new double[] { 59.0, 120.0 };
rawData[18] = new double[] { 68.0, 210.0 };
rawData[19] = new double[] { 61.0, 130.0 };
Console.WriteLine("Raw unclustered data:");
Console.WriteLine(" Height Weight");
Console.WriteLine("-------------------");
ShowData(rawData, 1, true, true);
int numClusters = 3;
Console.WriteLine("Setting numClusters to " + numClusters);
int[] clustering = Cluster(rawData, numClusters);
Console.WriteLine("K-means clustering complete");
Console.WriteLine("Final clustering in internal form:");
ShowVector(clustering, true);
Console.WriteLine("Raw data by cluster:");
ShowClustered(rawData, clustering, numClusters, 1);
Console.WriteLine("End k-means clustering demo");
Console.ReadLine();
}
public static int[] Cluster(double[][] rawData,
int numClusters) { . . }
private static double[][] Normalized(double[][] rawData) { . . }
private static int[] InitClustering(int numTuples,
int numClusters, int seed) { . . }
private static double[][] Allocate(int numClusters,
int numColumns) { . . }
private static bool UpdateMeans(double[][] data,
int[] clustering, double[][] means) { . . }
private static bool UpdateClustering(double[][] data,
int[] clustering, double[][] means) { . . }
private static double Distance(double[] tuple,
double[] mean) { . . }
private static int MinIndex(double[] distances) { . . }
static void ShowData(double[][] data, int decimals,
bool indices, bool newLine) { . . }
static void ShowVector(int[] vector, bool newLine) { . . }
static void ShowClustered(double[][] data, int[] clustering,
int numClusters, int decimals) { . . }
}
}
The demo program begins by setting up some data to be clustered:
double[][] rawData = new double[20][];
rawData[0] = new double[] { 65.0, 220.0 };
rawData[1] = new double[] { 73.0, 160.0 };
. . .
In most situations, your data will likely be stored in a text file or SQL database, and you'll have to write some code to load your data into memory. The data is stored into an array of arrays style matrix. Unlike most languages, C# has a true multidimensional array type, and you may want to use it instead. The two lines which cluster the data are:
int numClusters = 3;
int[] clustering = Cluster(rawData, numClusters);
The k-means algorithm requires the number of clusters to be specified in advance. The Cluster method returns an array that encodes cluster membership; the array index is the index of a data tuple, and the array cell value is a zero-based cluster ID. For example, the demo result is [1 0 2 2 0 1 . . 2], which means data[0] is assigned to cluster 1, data[1] is assigned to cluster 0, data[2] is assigned to cluster 2, and so on.
The Cluster Method
Method Cluster is very short because it uses five helper methods:
public static int[] Cluster(double[][] rawData, int numClusters)
{
double[][] data = Normalized(rawData);
bool changed = true; bool success = true;
int[] clustering = InitClustering(data.Length, numClusters, 0);
double[][] means = Allocate(numClusters, data[0].Length);
int maxCount = data.Length * 10;
int ct = 0;
while (changed == true && success == true && ct < maxCount) {
++ct;
success = UpdateMeans(data, clustering, means);
changed = UpdateClustering(data, clustering, means);
}
return clustering;
}
Cluster begins by calling a Normalized method that converts raw data such as {65.0, 220.0} into normalized data such as {-0.05, 0.02}. I'll explain the normalization process shortly. The Boolean variable named "changed" tracks whether or not any of the data tuples changed clusters, or equivalently, whether or not the clustering has changed. The Boolean variable "success" indicates whether the means of the clusters were able to be computed. Variables ct and maxCount are used to limit the number of times the clustering loop executes, essentially acting as a sanity check. The clustering loop exits when there's no change to the clustering, or one or more means cannot be computed because doing so would create a situation with no data tuples assigned to some cluster, or when maxCount iterations is reached.
Normalization
In situations where the components of a data tuple have different scales, such as the height-weight demo data, it's usually a good idea to normalize the data. The idea is that the component with larger values (weight in the demo) will overwhelm the component with smaller values.
There are several ways to normalize data. This demo uses Gaussian normalization. Each raw value v in a column is converted to a normalized value v' by subtracting the arithmetic mean of all the values in the column and then dividing by the standard deviation of the values. Normalized values will almost always be between -10 and +10. For raw data -- which follows a bell-shaped distribution -- most normalized values will be between -3 and +3. The Normalize method is presented in Listing 2.
Listing 2: The Normalize Method
private static double[][] Normalized(double[][] rawData)
{
double[][] result = new double[rawData.Length][];
for (int i = 0; i < rawData.Length; ++i)
{
result[i] = new double[rawData[i].Length];
Array.Copy(rawData[i], result[i], rawData[i].Length);
}
for (int j = 0; j < result[0].Length; ++j)
{
double colSum = 0.0;
for (int i = 0; i < result.Length; ++i)
colSum += result[i][j];
double mean = colSum / result.Length;
double sum = 0.0;
for (int i = 0; i < result.Length; ++i)
sum += (result[i][j] - mean) * (result[i][j] - mean);
double sd = sum / result.Length;
for (int i = 0; i < result.Length; ++i)
result[i][j] = (result[i][j] - mean) / sd;
}
return result;
}
The code presented in this article normalizes data inside the clustering method. An alternative is to normalize the raw data in a preprocessing step.
Cluster Initialization
Method InitClustering initializes the clustering array by assigning each data tuple to a randomly selected cluster ID. The method arbitrarily assigns tuples 0, 1 and 2 to clusters 0, 1 and 2, respectively, so that each cluster is guaranteed to have at least one data tuple assigned to it:
private static int[] InitClustering(int numTuples, int numClusters, int seed)
{
Random random = new Random(seed);
int[] clustering = new int[numTuples];
for (int i = 0; i < numClusters; ++i)
clustering[i] = i;
for (int i = numClusters; i < clustering.Length; ++i)
clustering[i] = random.Next(0, numClusters);
return clustering;
}
The final clustering result depends to a large extent on how the clustering is initialized. There are several approaches to initialization, but the technique presented here is the simplest and works well in practice.
One common alternative is to initialize cluster means, rather than cluster membership, by picking representative data tuples. The clustering pseudo-code becomes:
initialize means
loop
update clustering based on means
compute new means
end loop
Using this approach, the initial representative data tuples should be selected in such a way that they're different from each other.
Computing Cluster Means
Computing the mean of a cluster is best explained by example. Suppose a cluster has three height-weight tuples: d0 = {64, 110}, d1 = {65, 160}, d2 = {72, 180}. The mean of the cluster is computed as {(64+65+72)/3, (110+160+180)/3} = {67.0, 150.0}. In other words, you just compute the average of each data component. Method UpdateMeans is presented in Listing 3.
Listing 3: Method UpdateMeans
private static bool UpdateMeans(double[][] data, int[] clustering, double[][] means)
{
int numClusters = means.Length;
int[] clusterCounts = new int[numClusters];
for (int i = 0; i < data.Length; ++i)
{
int cluster = clustering[i];
++clusterCounts[cluster];
}
for (int k = 0; k < numClusters; ++k)
if (clusterCounts[k] == 0)
return false;
for (int k = 0; k < means.Length; ++k)
for (int j = 0; j < means[k].Length; ++j)
means[k][j] = 0.0;
for (int i = 0; i < data.Length; ++i)
{
int cluster = clustering[i];
for (int j = 0; j < data[i].Length; ++j)
means[cluster][j] += data[i][j]; // accumulate sum
}
for (int k = 0; k < means.Length; ++k)
for (int j = 0; j < means[k].Length; ++j)
means[k][j] /= clusterCounts[k]; // danger of div by 0
return true;
}
One of the potential pitfalls of the k-means algorithm is that all clusters must have at least one tuple assigned at all times. The first few lines of UpdateMeans scan the clustering input array parameter and count the number of tuples assigned to each cluster. If any cluster has no tuples assigned, the method exits and returns false. This is a fairly expensive operation and can be omitted if the methods that initialize the clustering and update the clustering both guarantee that there are no zero-count clusters.
Notice that matrix means is actually used as a C# style ref parameter -- the new means are stored into the parameter. So you might want to label the means parameter with the ref keyword to make this idea explicit.
In method Cluster, for convenience, the means matrix is allocated using helper method allocate:
private static double[][] Allocate(int numClusters, int numColumns)
{
double[][] result = new double[numClusters][];
for (int k = 0; k < numClusters; ++k)
result[k] = new double[numColumns];
return result;
}
Updating the Clustering
In each iteration of the Cluster method, after new cluster means have been computed, the cluster membership of each data tuple is updated in method UpdateClustering. Method UpdateClustering is presented in Listing 4.
Listing 4: The UpdateClustering Method
private static bool UpdateClustering(double[][] data, int[] clustering, double[][] means)
{
int numClusters = means.Length;
bool changed = false;
int[] newClustering = new int[clustering.Length];
Array.Copy(clustering, newClustering, clustering.Length);
double[] distances = new double[numClusters];
for (int i = 0; i < data.Length; ++i)
{
for (int k = 0; k < numClusters; ++k)
distances[k] = Distance(data[i], means[k]);
int newClusterID = MinIndex(distances);
if (newClusterID != newClustering[i])
{
changed = true;
newClustering[i] = newClusterID;
}
}
if (changed == false)
return false;
int[] clusterCounts = new int[numClusters];
for (int i = 0; i < data.Length; ++i)
{
int cluster = newClustering[i];
++clusterCounts[cluster];
}
for (int k = 0; k < numClusters; ++k)
if (clusterCounts[k] == 0)
return false;
Array.Copy(newClustering, clustering, newClustering.Length);
return true; // no zero-counts and at least one change
}
Method UpdateClustering uses the idea of the distance between a data tuple and a cluster mean. The Euclidean distance between two vectors is the square root of the sum of the squared differences between corresponding component values. For example, suppose some data tuple d0 = {68, 140} and three cluster means are c0 = {66.0, 120.0}, c1 = {69.0, 160.0}, and c2 = {70.0, 130.0}. (Note that I'm using raw, un-normalized data for demonstration purposes only.) The distance between d0 and c0 = sqrt((68 - 66.0)^2 + (140 - 120.0)^2) = 20.10. The distance between d0 and c1 = sqrt((68 - 69.0)^2 + (140 - 160.0)^2) = 20.22. And the distance between d0 and c2 = sqrt((68 - 70.0)^2 + (140 - 130.0)^2) = 10.20. The data tuple is closest to mean c2, and so would be assigned to cluster 2.
Method Distance is defined as:
private static double Distance(double[] tuple, double[] mean)
{
double sumSquaredDiffs = 0.0;
for (int j = 0; j < tuple.Length; ++j)
sumSquaredDiffs += Math.Pow((tuple[j] - mean[j]), 2);
return Math.Sqrt(sumSquaredDiffs);
}
Method UpdateClustering scans each data tuple, computes the distances from the current tuple to each of the cluster means, and then assigns the tuple to the closest mean using helper function MinIndex, defined as:
private static int MinIndex(double[] distances)
{
int indexOfMin = 0;
double smallDist = distances[0];
for (int k = 0; k < distances.Length; ++k) {
if (distances[k] < smallDist) {
smallDist = distances[k];
indexOfMin = k;
}
}
return indexOfMin;
}
Method UpdateClustering computes a proposed new clustering into local array newClustering, and then counts the number of tuples assigned to each cluster in the proposed clustering. If any clusters would have no data tuples assigned, UpdateClustering exits and returns false. Otherwise, the new clustering is copied into the clustering parameter. During the copy, the method tracks if there are any changes to cluster membership. If there are no changes, the method exits and returns false. Note that parameter clustering is a C# ref parameter, and you may want to label it explicitly.
Helper Display Methods
The demo program has three helper methods to display data. The methods are presented in Listing 5. Method ShowData displays a matrix of type double to the console. Method ShowVector displays an array of type int to the console. And method ShowClustered displays a matrix of type double, grouped by cluster membership.
Listing 5: Helper Display Methods
static void ShowData(double[][] data, int decimals,
bool indices, bool newLine)
{
for (int i = 0; i < data.Length; ++i)
{
if (indices) Console.Write(i.ToString().PadLeft(3) + " ");
for (int j = 0; j < data[i].Length; ++j)
{
if (data[i][j] >= 0.0) Console.Write(" ");
Console.Write(data[i][j].ToString("F" + decimals) + " ");
}
Console.WriteLine("");
}
if (newLine) Console.WriteLine("");
}
static void ShowVector(int[] vector, bool newLine)
{
for (int i = 0; i < vector.Length; ++i)
Console.Write(vector[i] + " ");
if (newLine) Console.WriteLine("\n");
}
static void ShowClustered(double[][] data, int[] clustering,
int numClusters, int decimals)
{
for (int k = 0; k < numClusters; ++k)
{
Console.WriteLine("===================");
for (int i = 0; i < data.Length; ++i)
{
int clusterID = clustering[i];
if (clusterID != k) continue;
Console.Write(i.ToString().PadLeft(3) + " ");
for (int j = 0; j < data[i].Length; ++j)
{
if (data[i][j] >= 0.0) Console.Write(" ");
Console.Write(data[i][j].ToString("F" + decimals) + " ");
}
Console.WriteLine("");
}
Console.WriteLine("===================");
} // k
}
Modifications and Extensions
The code presented here can be modified and extended in several ways. In some situations, you may be more interested in the final cluster means than in the clustering membership. In those situations, you can refactor method Cluster so that instead of returning an int array representing cluster membership, you return the means of the final clusters.
The UpdateClustering method uses Euclidean distance to assign cluster membership. Euclidean distance heavily penalizes outlier data tuples. In some situations, an alternative distance metric, such as the Manhattan distance, might be preferable.
With regards to performance, the UpdateClustering method is usually the most time-consuming part of the k-means algorithm. If you refer to Figure 5, you'll notice that each data tuple can be processed independently, so using the C# Parallel.For loop feature, available in .NET 4.0 and later, can improve performance dramatically in many cases.
The final clustering produced by the k-means algorithm depends on how clusters are initialized. It's unlikely, but possible, that k-means will generate a poor clustering. One approach for dealing with this is to modify method Cluster so that it returns a value that represents how well the data's been clustered, such as the average distance between data tuples within clusters (smaller values are better), or the average distance between cluster means (larger values are better). Then you can run k-means several times, with different initializations, and use the best clustering found.