Neural Network Lab
Neural Network Training Using Particle Swarm Optimization
Although mathematically elegant, back-propagation isn't perfect. Instead consider using particle swarm optimization (PSO) to train your neural network; here's how.
You can think of a neural network as a complex function that accepts some numeric inputs and that generates some numeric outputs. A neural network has weights and bias values that, along with the inputs, determine the outputs. In most cases, you want to create a neural network that will make predictions -- for example, predicting a person's political party affiliation (0 = Democrat, 1 = Republican, 2 = other) based on factors such as the person's age, annual income, sex and so on. To do this, you can use data that has known input and output values and find a set of weights and bias values so that your neural network generates computed outputs that closely match the known outputs. This process is called training the neural network. After the network has been trained with data that has known outputs, it can be presented with new data and predictions can be made.
There are several approaches for training a neural network. By far the most common technique is called back-propagation (view my article on this topic here). Although mathematically elegant, back-propagation isn't perfect. This article describes an alternative neural network training technique that uses particle swarm optimization (PSO).
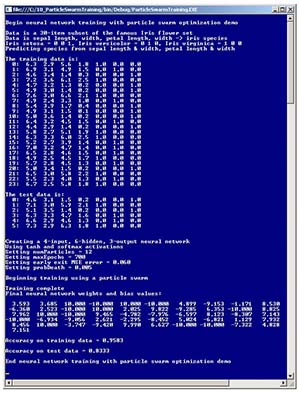
The best way to get an idea of what training a neural network using PSO is like is to take a look at a screenshot of a demo program shown in Figure 1. The demo program creates a neural network predictor for a set of Iris flowers, where the goal is to predict the species (setosa, versicolor or virginica) based on sepal (green covering) length and width, and petal (the flower part) length and width. The data is encoded so that (0,0,1) represents setosa, (0,1,0) is versicolor and (1,0,0) is virginica.
 [Click on image for larger view.]
Figure 1. Training a neural network using PSO.
[Click on image for larger view.]
Figure 1. Training a neural network using PSO.
The demo program uses an artificially small, 30-item subset of a famous 150-item benchmark data set called Fisher's Iris data. The data is randomly assigned so that 80 percent (24 items) are used for training, and the remaining 20 percent (six items) are used for testing. A 4-input, 6-hidden, 3-output neural network is instantiated. A fully-connected 4-6-3 neural network will have (4 * 6) + (6 * 3) + (6 + 3) = 51 weights and bias values. The demo creates a swarm consisting of 12 virtual particles, and the swarm attempts to find the set of neural network weights and bias values in a maximum of 700 iterations. After PSO training has completed, the 51 values of the best weights and biases that were found are displayed. Using those weights and biases, when the neural network is fed the six training items, the network correctly classifies 5/6 = 0.8333 of the items, as shown in Figure 1.
This article explains how particle swarm optimization can be used to train a neural network and presents the complete source code for the demo program. This article focuses on PSO and assumes you have a solid grasp of the neural network input-process-output mechanism and that you have advanced programming skills. The demo download is coded using C#, but you should be able to refactor the demo to another language, such as JavaScript or Python, without too much difficulty. Most normal error-checking code has been removed to keep the size of the demo small and the main ideas clear.
Particle Swarm Optimization
PSO is a technique that is loosely modeled on the coordinated behavior of groups, such as flocks of birds and schools of fish. Each particle has a virtual position that represents a possible solution to some minimization problem. In the case of a neural network, a particle's position represents the values for the network's weights and biases. The goal is to find a position/weights so that the network generates computed outputs that match the outputs of the training data.
PSO uses a collection of particles and is an iterative process. In each iteration, every particle moves to a new position which, hopefully, represents a better problem solution. A particle's movement is based on the particle's current speed and direction (velocity), the best position found by the particle at any time and the best position found by any of the other particles in the swarm.
In very high-level pseudo-code, PSO looks something like this:
initialize each particle to random state
(position, velocity, error, best-position, best-error)
save best position of any particle (global-best)
loop until done
for each particle in swarm
compute new particle velocity
use new velocity to compute new position
compute error of new position
if new error better than best-error
best-position = new position
if new error better than global-best
global-best = new position
end for
end loop
return global-best position
The key to PSO is the computation of a particle's new velocity. Expressed in math terms, the velocity and position update equations are:
v(t+1) = (w * v(t)) + (c1 * r1 * (p(t) – x(t)) + (c2 * r2 * (g(t) – x(t))
x(t+1) = x(t) + v(t+1)
The update process is actually much simpler than these equations suggest. The first equation updates a particle's velocity. The term v(t+1) is the velocity at time t+1. Notice that v is in bold, indicating that velocity is a vector value and has multiple components such as (1.55, -0.33) rather than being a single scalar value. The new velocity depends on three terms. The first term is w * v(t). The w factor is called the inertia weight and is just a constant like 0.73, and v(t) is the current velocity at time t.
The second term is c1 * r1 * (p(t) – x(t)). The c1 factor is a constant called the cognitive (or personal or local) weight. The r1 factor is a random variable in the range [0, 1) -- that is, greater than or equal to 0 and strictly less than 1. The p(t) vector value is the particle's best position found so far. The x(t) vector value is the particle's current position.
The third term in the velocity update equation is (c2 * r2 * (g(t) – x(t)). The c2 factor is a constant called the social, or global, weight. The r2 factor is a random variable in the range [0, 1). The g(t) vector value is the best known position found by any particle in the swarm so far. Once the new velocity, v(t+1) has been determined, it is used to compute the new particle position x(t+1).
A concrete example will help make the update process clear. Suppose that you're trying to minimize some error function that depends on two x-values, x0 and x1, and that has a minimum value at x0 = 0.0 and x1 = 0.0.
Let's say that a particle's current position, x(t), is {x0, x1} = {3.0, 4.0}, and that the particle's current velocity, v(t), is {-1.0, -1.5}. Additionally, assume that constant w = 0.7, constant c1 = 1.4, constant c2 = 1.4, and that random numbers r1 and r2 are 0.5 and 0.6, respectively. Finally, suppose that the particle's best known position is p(t) = {2.5, 3.6} and that the global best known position by any particle in the swarm is g(t) = {2.3, 3.4}. Then, the new velocity and position values are:
v(t+1) = (0.7 * {-1.0,-1.5}) +
(1.4 * 0.5 * {2.5, 3.6} - {3.0, 4.0}) +
(1.4 * 0.6 * {2.3, 3.4} – {3.0, 4.0})
= {-0.70, -1.05} + {-0.35, -0.28} + {-0.59, -0.50}
= {-1.64, -1.83}.
x(t+1) = {3.0, 4.0} + {-1.64, -1.83}
= {1.36, 2.17}.
Recall that the optimal solution is {x0, x1} = (0.0, 0.0}. Observe that the update process has improved the old position/solution from (3.0, 4.0} to {1.36, 2.17}. If you examine the update process a bit, you'll see that the new velocity is the old velocity (times a weight) plus a factor which depends on a particle's best known position, plus another factor which depends on the best known position from all particles in the swarm. A particle's new position tends to move toward a better position based on the particle's best known position and the best known position from all particles.
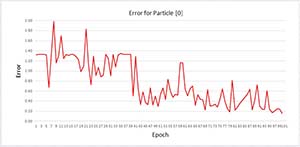
The graph in Figure 2 shows how the error term for particle [0] changes during the first 100 epochs of the demo run. The large upward spikes in error tend to occur when the particle dies and is reborn at a new position. Notice that although the error does tend to jump around, the overall trend is to continuously find positions with smaller error.
 [Click on image for larger view.]
Figure 2. Particle [0] error by epoch.
[Click on image for larger view.]
Figure 2. Particle [0] error by epoch.
Demo Program Structure
The overall structure of the demo program, with a few minor edits to save space, is shown in Listing 1. To create the demo, I launched Visual Studio and created a new console application named ParticleSwarmTraining. The program has no significant .NET dependencies and any version of Visual Studio should work. In the Solution Explorer window, I renamed file Program.cs to ParticleTrainingProgram.cs and Visual Studio automatically rented class Program for me.
Listing 1: Neural Network with PSO Training Program
using System;
namespace ParticleSwarmTraining
{
class ParticleTrainingProgram
{
static void Main(string[] args)
{
Console.WriteLine("Begin neural network training demo");
Console.WriteLine("Data is 30-item subset of Iris flower set");
Console.Write("Data is sepal length, width, petal length, width");
Console.WriteLine(" -> iris species");
Console.Write("Iris setosa = 0 0 1, Iris versicolor = 0 1 0,");
Console.WriteLine(" Iris virginica = 1 0 0 ");
Console.WriteLine("Predicting species");
double[][] trainData = new double[24][];
trainData[0] = new double[] { 6.3, 2.9, 5.6, 1.8, 1, 0, 0 };
trainData[1] = new double[] { 6.9, 3.1, 4.9, 1.5, 0, 1, 0 };
trainData[2] = new double[] { 4.6, 3.4, 1.4, 0.3, 0, 0, 1 };
trainData[3] = new double[] { 7.2, 3.6, 6.1, 2.5, 1, 0, 0 };
trainData[4] = new double[] { 4.7, 3.2, 1.3, 0.2, 0, 0, 1 };
trainData[5] = new double[] { 4.9, 3, 1.4, 0.2, 0, 0, 1 };
trainData[6] = new double[] { 7.6, 3, 6.6, 2.1, 1, 0, 0 };
trainData[7] = new double[] { 4.9, 2.4, 3.3, 1, 0, 1, 0 };
trainData[8] = new double[] { 5.4, 3.9, 1.7, 0.4, 0, 0, 1 };
trainData[9] = new double[] { 4.9, 3.1, 1.5, 0.1, 0, 0, 1 };
trainData[10] = new double[] { 5, 3.6, 1.4, 0.2, 0, 0, 1 };
trainData[11] = new double[] { 6.4, 3.2, 4.5, 1.5, 0, 1, 0 };
trainData[12] = new double[] { 4.4, 2.9, 1.4, 0.2, 0, 0, 1 };
trainData[13] = new double[] { 5.8, 2.7, 5.1, 1.9, 1, 0, 0 };
trainData[14] = new double[] { 6.3, 3.3, 6, 2.5, 1, 0, 0 };
trainData[15] = new double[] { 5.2, 2.7, 3.9, 1.4, 0, 1, 0 };
trainData[16] = new double[] { 7, 3.2, 4.7, 1.4, 0, 1, 0 };
trainData[17] = new double[] { 6.5, 2.8, 4.6, 1.5, 0, 1, 0 };
trainData[18] = new double[] { 4.9, 2.5, 4.5, 1.7, 1, 0, 0 };
trainData[19] = new double[] { 5.7, 2.8, 4.5, 1.3, 0, 1, 0 };
trainData[20] = new double[] { 5, 3.4, 1.5, 0.2, 0, 0, 1 };
trainData[21] = new double[] { 6.5, 3, 5.8, 2.2, 1, 0, 0 };
trainData[22] = new double[] { 5.5, 2.3, 4, 1.3, 0, 1, 0 };
trainData[23] = new double[] { 6.7, 2.5, 5.8, 1.8, 1, 0, 0 };
double[][] testData = new double[6][];
testData[0] = new double[] { 4.6, 3.1, 1.5, 0.2, 0, 0, 1 };
testData[1] = new double[] { 7.1, 3, 5.9, 2.1, 1, 0, 0 };
testData[2] = new double[] { 5.1, 3.5, 1.4, 0.2, 0, 0, 1 };
testData[3] = new double[] { 6.3, 3.3, 4.7, 1.6, 0, 1, 0 };
testData[4] = new double[] { 6.6, 2.9, 4.6, 1.3, 0, 1, 0 };
testData[5] = new double[] { 7.3, 2.9, 6.3, 1.8, 1, 0, 0 };
Console.WriteLine("The training data is:");
ShowMatrix(trainData, trainData.Length, 1, true);
Console.WriteLine("The test data is:");
ShowMatrix(testData, testData.Length, 1, true);
Console.WriteLine("Creating a 4-6-3 neural network");
Console.WriteLine("Using tanh and softmax activations");
const int numInput = 4;
const int numHidden = 6;
const int numOutput = 3;
NeuralNetwork nn =
new NeuralNetwork(numInput, numHidden, numOutput);
int numParticles = 12;
int maxEpochs = 700;
double exitError = 0.060;
double probDeath = 0.005;
Console.WriteLine("Setting numParticles = " +
numParticles);
Console.WriteLine("Setting maxEpochs = " + maxEpochs);
Console.Write("Setting early exit MSE error = ");
Console.WriteLine(exitError.ToString("F3"));
Console.Write("Setting probDeath = ");
Console.WriteLine(probDeath.ToString("F3"));
Console.WriteLine("Beginning training");
double[] bestWeights =
nn.Train(trainData, numParticles, maxEpochs,
exitError, probDeath);
Console.WriteLine("Training complete");
Console.WriteLine("Final weights and bias values:");
ShowVector(bestWeights, 10, 3, true);
nn.SetWeights(bestWeights);
double trainAcc = nn.Accuracy(trainData);
Console.Write("Accuracy on training data = ");
Console.WriteLine( trainAcc.ToString("F4"));
double testAcc = nn.Accuracy(testData);
Console.WriteLine("Accuracy on test data = ");
Console.WriteLine(testAcc.ToString("F4"));
Console.WriteLine("End demo");
Console.ReadLine();
} // Main
static void ShowVector(double[] vector, int valsPerRow,
int decimals, bool newLine)
{
for (int i = 0; i < vector.Length; ++i)
{
if (i % valsPerRow == 0) Console.WriteLine("");
Console.Write(vector[i].ToString("F" + decimals));
}
if (newLine == true)
Console.WriteLine("");
}
static void ShowMatrix(double[][] matrix, int numRows,
int decimals, bool newLine)
{
for (int i = 0; i < numRows; ++i)
{
Console.Write(i.ToString().PadLeft(3) + ": ");
for (int j = 0; j < matrix[i].Length; ++j)
{
if (matrix[i][j] >= 0.0)
Console.Write(" ");
else
Console.Write("-"); ;
Console.Write(Math.Abs(matrix[i][j]));
}
Console.WriteLine("");
}
if (newLine == true)
Console.WriteLine("");
}
} // class Program
public class NeuralNetwork
{
private int numInput;
private int numHidden;
private int numOutput;
private double[] inputs;
private double[][] ihWeights;
private double[] hBiases;
private double[] hOutputs;
private double[][] hoWeights;
private double[] oBiases;
private double[] outputs;
public NeuralNetwork(int numInput, int numHidden,
int numOutput)
{
this.numInput = numInput;
this.numHidden = numHidden;
this.numOutput = numOutput;
this.inputs = new double[numInput];
this.ihWeights = MakeMatrix(numInput, numHidden);
this.hBiases = new double[numHidden];
this.hOutputs = new double[numHidden];
this.hoWeights = MakeMatrix(numHidden, numOutput);
this.oBiases = new double[numOutput];
this.outputs = new double[numOutput];
} // ctor
private static double[][] MakeMatrix(int rows, int cols)
{
double[][] result = new double[rows][];
for (int r = 0; r < result.Length; ++r)
result[r] = new double[cols];
return result;
}
public void SetWeights(double[] weights)
{
int numWeights = (numInput * numHidden) +
(numHidden * numOutput) + numHidden + numOutput;
if (weights.Length != numWeights)
throw new Exception("Bad weights array length: ");
int k = 0; // points into weights param
for (int i = 0; i < numInput; ++i)
for (int j = 0; j < numHidden; ++j)
ihWeights[i][j] = weights[k++];
for (int i = 0; i < numHidden; ++i)
hBiases[i] = weights[k++];
for (int i = 0; i < numHidden; ++i)
for (int j = 0; j < numOutput; ++j)
hoWeights[i][j] = weights[k++];
for (int i = 0; i < numOutput; ++i)
oBiases[i] = weights[k++];
}
public double[] GetWeights()
{
int numWeights = (numInput * numHidden) +
(numHidden * numOutput) + numHidden + numOutput;
double[] result = new double[numWeights];
int k = 0;
for (int i = 0; i < ihWeights.Length; ++i)
for (int j = 0; j < ihWeights[0].Length; ++j)
result[k++] = ihWeights[i][j];
for (int i = 0; i < hBiases.Length; ++i)
result[k++] = hBiases[i];
for (int i = 0; i < hoWeights.Length; ++i)
for (int j = 0; j < hoWeights[0].Length; ++j)
result[k++] = hoWeights[i][j];
for (int i = 0; i < oBiases.Length; ++i)
result[k++] = oBiases[i];
return result;
}
public double[] ComputeOutputs(double[] xValues)
{
if (xValues.Length != numInput)
throw new Exception("Bad xValues array length");
double[] hSums = new double[numHidden];
double[] oSums = new double[numOutput];
for (int i = 0; i < xValues.Length; ++i)
this.inputs[i] = xValues[i];
for (int j = 0; j < numHidden; ++j)
for (int i = 0; i < numInput; ++i)
hSums[j] += this.inputs[i] * this.ihWeights[i][j];
for (int i = 0; i < numHidden; ++i)
hSums[i] += this.hBiases[i];
for (int i = 0; i < numHidden; ++i)
this.hOutputs[i] = HyperTanFunction(hSums[i]);
for (int j = 0; j < numOutput; ++j)
for (int i = 0; i < numHidden; ++i)
oSums[j] += hOutputs[i] * hoWeights[i][j];
for (int i = 0; i < numOutput; ++i)
oSums[i] += oBiases[i];
double[] softOut = Softmax(oSums);
Array.Copy(softOut, outputs, softOut.Length);
double[] retResult = new double[numOutput];
Array.Copy(this.outputs, retResult, retResult.Length);
return retResult;
} // ComputeOutputs
private static double HyperTanFunction(double x)
{
if (x < -20.0) return -1.0;
else if (x > 20.0) return 1.0;
else return Math.Tanh(x);
}
private static double[] Softmax(double[] oSums)
{
double max = oSums[0];
for (int i = 0; i < oSums.Length; ++i)
if (oSums[i] > max) max = oSums[i];
// determine scaling factor
double scale = 0.0;
for (int i = 0; i < oSums.Length; ++i)
scale += Math.Exp(oSums[i] - max);
double[] result = new double[oSums.Length];
for (int i = 0; i < oSums.Length; ++i)
result[i] = Math.Exp(oSums[i] - max) / scale;
return result; // scaled so xi sum to 1.0
}
public double[] Train(double[][] trainData,
int numParticles, int maxEpochs, double exitError,
double probDeath)
{
// use PSO to train
}
private static void Shuffle(int[] sequence, Random rnd)
{
for (int i = 0; i < sequence.Length; ++i)
{
int r = rnd.Next(i, sequence.Length);
int tmp = sequence[r];
sequence[r] = sequence[i];
sequence[i] = tmp;
}
}
private double MeanSquaredError(double[][] trainData,
double[] weights)
{
this.SetWeights(weights);
double[] xValues = new double[numInput]; // inputs
double[] tValues = new double[numOutput]; // targets
double sumSquaredError = 0.0;
for (int i = 0; i < trainData.Length; ++i)
{
// assumes data has x-values followed by y-values
Array.Copy(trainData[i], xValues, numInput);
Array.Copy(trainData[i], numInput, tValues, 0,
numOutput);
double[] yValues = this.ComputeOutputs(xValues);
for (int j = 0; j < yValues.Length; ++j)
sumSquaredError += ((yValues[j] - tValues[j]) *
(yValues[j] - tValues[j]));
}
return sumSquaredError / trainData.Length;
}
public double Accuracy(double[][] testData)
{
// percentage correct using winner-takes all
int numCorrect = 0;
int numWrong = 0;
double[] xValues = new double[numInput]; // inputs
double[] tValues = new double[numOutput]; // targets
double[] yValues; // computed Y
for (int i = 0; i < testData.Length; ++i)
{
Array.Copy(testData[i], xValues, numInput);
Array.Copy(testData[i], numInput, tValues, 0,
numOutput);
yValues = this.ComputeOutputs(xValues);
int maxIndex = MaxIndex(yValues);
if (tValues[maxIndex] == 1.0)
++numCorrect;
else
++numWrong;
}
return (numCorrect * 1.0) / (numCorrect + numWrong);
}
private static int MaxIndex(double[] vector)
{
int bigIndex = 0;
double biggestVal = vector[0];
for (int i = 0; i < vector.Length; ++i)
{
if (vector[i] > biggestVal)
{
biggestVal = vector[i]; bigIndex = i;
}
}
return bigIndex;
}
} // NeuralNetwork
public class Particle
{
public double[] position; // equivalent to NN weights
public double error; // measure of fitness
public double[] velocity;
public double[] bestPosition; // by this Particle
public double bestError;
public Particle(double[] position, double error,
double[] velocity, double[] bestPosition,
double bestError)
{
this.position = new double[position.Length];
position.CopyTo(this.position, 0);
this.error = error;
this.velocity = new double[velocity.Length];
velocity.CopyTo(this.velocity, 0);
this.bestPosition = new double[bestPosition.Length];
bestPosition.CopyTo(this.bestPosition, 0);
this.bestError = bestError;
}
} // class Particle
} // ns
The Train Method
The key lines in the demo program that perform neural network training using PSO are:
int numParticles = 12;
int maxEpochs = 700;
double exitError = 0.060;
double probDeath = 0.005;
double[] bestWeights =
nn.Train(trainData, numParticles, maxEpochs,
exitError, probDeath);
Most of the methods in class NeuralNework are common to any feed-forward neural network. These include SetWeights, GetWeights and ComputeOutputs. The methods that are specific to training the neural network using PSO are Train and its two helper methods, Shuffle and MeanSquaredError.
The signature for method Train is:
public double[] Train(double[][] trainData, int numParticles,
int maxEpochs, double exitError, double probDeath)
{
. . .
Input parameters maxEpochs and exitError control when the iterative PSO process will terminate. PSO is really a meta-heuristic, meaning that it's a set of guidelines and that there are many possible implementations. Input parameter probDeath is an option to control when particles will randomly die.
Method train first sets up some local values:
Random rnd = new Random(16);
int numWeights = (this.numInput * this.numHidden) +
(this.numHidden * this.numOutput) + this.numHidden + this.numOutput;
int epoch = 0;
double minX = -10.0;
double maxX = 10.0;
double w = 0.729; // inertia weight
double c1 = 1.49445; // cognitive weight
double c2 = 1.49445; // social weight
double r1, r2; // randomizations
. . .
Random object rnd is used to initialize particles to random positions and to control the death/birth mechanism; the object was seeded with 16 only because that value gave a nice demo. Variable epoch is the main loop counter. Variables minX and maxX give limits on the components of a particle's position. Because a position represents a set of weights and bias values, the constraints limit the range of weight and bias values. The inertia, cognitive and social weight values are some that have been recommended by research, but in general, unlike back-propagation, PSO is quite insensitive to the values used for these free parameters.
Next, method Train sets up the swarm and global best position and error:
Particle[] swarm = new Particle[numParticles];
double[] bestGlobalPosition = new double[numWeights];
double bestGlobalError = double.MaxValue;
The particle initialization code comes next; it's a bit longer than you might expect. Initialization starts:
for (int i = 0; i < swarm.Length; ++i)
{
double[] randomPosition = new double[numWeights];
for (int j = 0; j < randomPosition.Length; ++j)
{
randomPosition[j] = (maxX - minX) *
rnd.NextDouble() + minX;
}
double error = MeanSquaredError(trainData,
randomPosition);
. . .
First a random position is generated, then the associated error of the random position is computed. Here the mean squared error is used. For example, if one target output is (0,0,1) for setosa, and the computed output is (0.2, 0.1, 0.7), then the squared error is (0.2 - 0)^2 + (0.1 - 0)^2 + (0.7 - 1)^2 = 0.04 + 0.01 + 0.09 = 0.14. Mean squared error is the average of all errors on the training data.
The initialization process continues by determining a random velocity:
double[] randomVelocity = new double[numWeights];
for (int j = 0; j < randomVelocity.Length; ++j)
{
double lo = 0.1 * minX;
double hi = 0.1 * maxX;
randomVelocity[j] = (hi - lo) *
rnd.NextDouble() + lo;
}
. . .
Here the limits on the velocity components are set to one-tenth of the limits on the position components, but this is somewhat arbitrary in that any small initial value will work.
The initialization phase of method Train concludes with:
swarm[i] = new Particle(randomPosition, error,
randomVelocity, randomPosition, error);
if (swarm[i].error < bestGlobalError)
{
bestGlobalError = swarm[i].error;
swarm[i].position.CopyTo(bestGlobalPosition, 0);
}
}
// end initialization
. . .
The current particle is created using the Particle constructor, and the position of the newly-created particle is examined to see if it's the best position of any of the particles in the swarm.
After initialization, method Train prepares the main PSO processing loop:
int[] sequence = new int[numParticles];
for (int i = 0; i < sequence.Length; ++i)
sequence[i] = i;
while (epoch < maxEpochs)
{
if (bestGlobalError < exitError) break;
. . .
Based on my experience with PSO, neural network training is more efficient when the training data is examined by the particles in a random order. Array sequence holds indices of the particles and will be shuffled each time through the main processing loop. At the top of the processing loop, the best global error, found by any particle, is checked to see if it is small enough to meet the early exit criterion.
Inside the main loop, a new velocity, position and error are readied for the current particle. Then, each particle is updated in a random order:
Shuffle(sequence, rnd); // randomize particle order
double[] newVelocity = new double[numWeights];
double[] newPosition = new double[numWeights];
double newError; // step 3
for (int pi = 0; pi < swarm.Length; ++pi)
{
int i = sequence[pi];
Particle currP = swarm[i];
. . .
In the inner each-particle loop, a new velocity is computed:
for (int j = 0; j < currP.velocity.Length; ++j)
{
r1 = rnd.NextDouble();
r2 = rnd.NextDouble();
newVelocity[j] = (w * currP.velocity[j]) +
(c1 * r1 * (currP.bestPosition[j] - currP.position[j])) +
(c2 * r2 * (bestGlobalPosition[j] - currP.position[j]));
}
newVelocity.CopyTo(currP.velocity, 0);
. . .
Next, the new velocity is used to compute a new position:
for (int j = 0; j < currP.position.Length; ++j)
{
newPosition[j] = currP.position[j] + newVelocity[j];
if (newPosition[j] < minX) // keep in range
newPosition[j] = minX;
else if (newPosition[j] > maxX)
newPosition[j] = maxX;
}
newPosition.CopyTo(currP.position, 0);
. . .
Following that, the error associated with the new position is computed and checked to see if it's a particle-best or global-best error:
newError = MeanSquaredError(trainData, newPosition);
currP.error = newError;
if (newError < currP.bestError) // particle best?
{
newPosition.CopyTo(currP.bestPosition, 0);
currP.bestError = newError;
}
if (newError < bestGlobalError) // global best?
{
newPosition.CopyTo(bestGlobalPosition, 0);
bestGlobalError = newError;
}
. . .
The inner each-particle loop finishes up by randomly, with a small probability, killing off the current particle and giving birth to a new particle. This process helps prevent the PSO algorithm from getting stuck at non-optimal solutions:
double die = rnd.NextDouble();
if (die < probDeath)
{
// new position, leave velocity, update error
for (int j = 0; j < currP.position.Length; ++j)
currP.position[j] = (maxX - minX) * rnd.NextDouble() + minX;
currP.error = MeanSquaredError(trainData, currP.position);
currP.position.CopyTo(currP.bestPosition, 0);
currP.bestError = currP.error;
if (currP.error < bestGlobalError) // global best?
{
bestGlobalError = currP.error;
currP.position.CopyTo(bestGlobalPosition, 0);
}
}
} // each Particle
. . .
Method Train concludes by updating the loop counter, and copying the best found position into the neural network and also passing to a return result:
. . .
++epoch;
} // main while loop
this.SetWeights(bestGlobalPosition);
double[] retResult = new double[numWeights];
Array.Copy(bestGlobalPosition, retResult, retResult.Length);
return retResult;
} // Train
Particle Swarm Optimization vs. Back-Propagation
There are several reasons why you might want to consider using PSO rather than back-propagation to train a neural network. Based on my experience, back-propagation is extremely sensitive to the values used for the initial weights, the learning rate and, if used, the momentum. In some situations, making a slight change to any of these values makes a huge difference in the predictive accuracy of the neural network being trained. PSO tends to be much less sensitive with respect to its free parameters.
However, PSO does have disadvantages compared to back-propagation. The primary disadvantage of PSO, in my opinion, is that in most cases using PSO to train a neural network takes quite a bit longer than using back-propagation. In situations where I can afford the training time (which varies greatly from problem to problem), I tend to prefer PSO to back-propagation.