Neural Network Lab
Deep Neural Networks: A Getting Started Tutorial
Deep Neural Networks are the more computationally powerful cousins to regular neural networks. Learn exactly what DNNs are and why they are the hottest topic in machine learning research.
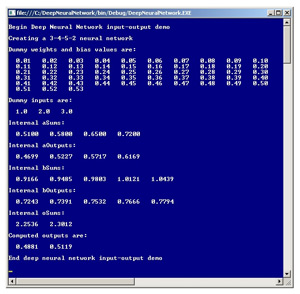
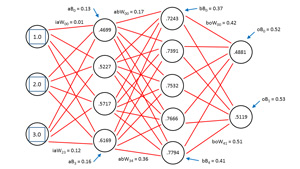
The term deep neural network can have several meanings, but one of the most common is to describe a neural network that has two or more layers of hidden processing neurons. This article explains how to create a deep neural network using C#. The best way to get a feel for what a deep neural network is and to see where this article is headed is to take a look at the demo program in Figure 1 and the associated diagram in Figure 2.
Both figures illustrate the input-output mechanism for a neural network that has three inputs, a first hidden layer ("A") with four neurons, a second hidden layer ("B") with five neurons and two outputs. "There are several different meanings for exactly what a deep neural network is, but one is just a neural network with two (or more) layers of hidden nodes." 3-4-5-2 neural network requires a total of (3 * 4) + 4 + (4 * 5) + 5 + (5 * 2) + 2 = 53 weights and bias values. In the demo, the weights and biases are set to dummy values of 0.01, 0.02, . . . , 0.53. The three inputs are arbitrarily set to 1.0, 2.0 and 3.0. Behind the scenes, the neural network uses the hyperbolic tangent activation function when computing the outputs of the two hidden layers, and the softmax activation function when computing the final output values. The two output values are 0.4881 and 0.5119.
 [Click on image for larger view.]
Figure 1. Deep Neural Network Demo
[Click on image for larger view.]
Figure 1. Deep Neural Network Demo
 [Click on image for larger view.]
Figure 2. Deep Neural Network Architecture
[Click on image for larger view.]
Figure 2. Deep Neural Network Architecture
Research in the field of deep neural networks is relatively new compared to classical statistical techniques. The so-called Cybenko theorem states, somewhat loosely, that a fully connected feed-forward neural network with a single hidden layer can approximate any continuous function. The point of using a neural network with two layers of hidden neurons rather than a single hidden layer is that a two-hidden-layer neural network can, in theory, solve certain problems that a single-hidden-layer network cannot. Additionally, a two-hidden-layer neural network can sometimes solve problems that would require a huge number of nodes in a single-hidden-layer network.
This article assumes you have a basic grasp of neural network concepts and terminology and at least intermediate-level programming skills. The demo is coded using C#, but you should be able to refactor the code to other languages such as JavaScript or Visual Basic .NET without too much difficulty. Most normal error checking has been omitted from the demo to keep the size of the code small and the main ideas as clear as possible.
The Input-Output Mechanism
The input-output mechanism for a deep neural network with two hidden layers is best explained by example. Take a look at Figure 2. Because of the complexity of the diagram, most of the weights and bias value labels have been omitted, but because the values are sequential -- from 0.01 through 0.53 -- you should be able to infer exactly what the unlabeled values are. Nodes, weights and biases are indexed (zero-based) from top to bottom. The first hidden layer is called layer A in the demo code and the second hidden layer is called layer B. For example, the top-most input node has index [0] and the bottom-most node in the second hidden layer has index [4].
In the diagram, label iaW00 means, "input to layer A weight from input node 0 to A node 0." Label aB0 means, "A layer bias value for A node 0." The output for layer-A node [0] is 0.4699 and is computed as follows (first, the sum of the node's inputs times associated with their weights is computed):
(1.0)(0.01) + (2.0)(0.05) + (3.0)(0.09) = 0.38
Next, the associated bias is added:
0.38 + 0.13 = 0.51
Then, the hyperbolic tangent function is applied to the sum to give the node's local output value:
tanh(0.51) = 0.4699
The three other values for the layer-A hidden nodes are computed in the same way, and are 0.5227, 0.5717 and 0.6169, as you can see in both Figure 1 and Figure 2. Notice that the demo treats bias values as separate constants, rather than the somewhat confusing and common alternative of treating bias values as special weights associated with dummy constant 1.0-value inputs.
The output for layer-B node [0] is 0.7243. The node's intermediate sum is:
(0.4699)(0.17) + (0.5227)(0.22) + (0.5717)(0.27) + (0.6169)(0.32) = 0.5466
The bias is added:
0.5466 + 0.37 = 0.9166
And the hyperbolic tangent is applied:
tanh(0.9166) = 0.7243
The same pattern is followed to compute the other layer-B hidden node values: 0.7391, 0.7532, 0.7666 and 0.7794. The values for final output nodes [0] and [1] are computed in a slightly different way because softmax activation is used to coerce the sum of the outputs to 1.0. Preliminary (before activation) output [0] is:
(0.7243)(0.42) + (0.7391)(0.44) + (0.7532)(0.46) + (0.7666)(0.48) + (0.7794)(0.50) + 0.52 = 2.2536
Similarly, preliminary output [1] is:
(0.7243)(0.43) + (0.7391)(0.45) + (0.7532)(0.47) + (0.7666)(0.49) + (0.7794)(0.51) + 0.53 = 2.3012
Applying softmax, final output [0] = exp(2.2536) / (exp(2.2536) + exp(2.3012)) = 0.4881. And final output [1] = exp(2.3012) / (exp(2.2536) + exp(2.3012)) = 0.5119
The two final output computations are illustrated using the math definition of softmax activation. The demo program uses a derivation of the definition to avoid arithmetic overflow.
Overall Program Structure
The overall structure of the demo program, with a few minor edits to save space, is presented in Listing 1. To create the demo, I launched Visual Studio and created a new project named DeepNeuralNetwork. The demo has no significant Microsoft .NET Framework version dependencies, so any relatively recent version of Visual Studio should work. After the template-generated code loaded into the editor, I removed all using statements except the one that references the top-level System namespace. In the Solution Explorer window I renamed the file Program.cs to the slightly more descriptive DeepNetProgram and Visual Studio automatically renamed class Program for me.
Listing 1: Overall Demo Program Structure
using System;
namespace DeepNeuralNetwork
{
class DeepNetProgram
{
static void Main(string[] args)
{
Console.WriteLine("Begin Deep Neural Network demo");
Console.WriteLine("Creating a 3-4-5-2 network");
int numInput = 3;
int numHiddenA = 4;
int numHiddenB = 5;
int numOutput = 2;
DeepNeuralNetwork dnn =
new DeepNeuralNetwork(numInput,
numHiddenA, numHiddenB, numOutput);
double[] weights = new double[] {
0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.10,
0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18, 0.19, 0.20,
0.21, 0.22, 0.23, 0.24, 0.25, 0.26, 0.27, 0.28, 0.29, 0.30,
0.31, 0.32, 0.33, 0.34, 0.35, 0.36, 0.37, 0.38, 0.39, 0.40,
0.41, 0.42, 0.43, 0.44, 0.45, 0.46, 0.47, 0.48, 0.49, 0.50,
0.51, 0.52, 0.53 };
dnn.SetWeights(weights);
double[] xValues = new double[] { 1.0, 2.0, 3.0 };
Console.WriteLine("Dummy weights and bias values are:");
ShowVector(weights, 10, 2, true);
Console.WriteLine("Dummy inputs are:");
ShowVector(xValues, 3, 1, true);
double[] yValues = dnn.ComputeOutputs(xValues);
Console.WriteLine("Computed outputs are:");
ShowVector(yValues, 2, 4, true);
Console.WriteLine("End deep neural network demo");
Console.ReadLine();
}
static public void ShowVector(double[] vector, int valsPerRow,
int decimals, bool newLine)
{
for (int i = 0; i < vector.Length; ++i)
{
if (i % valsPerRow == 0) Console.WriteLine("");
Console.Write(vector[i].ToString("F" + decimals) + " ");
}
if (newLine == true) Console.WriteLine("");
}
} // Program
public class DeepNeuralNetwork { . . }
}
The program class consists of the Main entry point method and a ShowVector helper method. The deep neural network is encapsulated in a program-defined class named DeepNeuralNetwork. The Main method instantiates a 3-4-5-2 fully connected feed-forward neural network and assigns 53 dummy values for the network's weights and bias values using method SetWeights. After dummy inputs of 1.0, 2.0 and 3.0 are set up in array xValues, those inputs are fed to the network via method ComputeOutputs, which returns the outputs into array yValues. Notice that the demo illustrates only the deep neural network feed-forward mechanism, and doesn't perform any training.
The Deep Neural Network Class
The structure of the deep neural network class is presented in Listing 2. The network is hard-coded for two hidden layers. Neural networks with three or more hidden layers are rare, but can be easily created using the design pattern in this article. A challenge when working with deep neural networks is keeping the names of the many weights, biases, inputs and outputs straight. The input-to-layer-A weights are stored in matrix iaWeights, the layer-A-to-layer-B weights are stored in matrix abWeights, and the layer-B-to-output weights are stored in matrix boWeights.
Listing 2: Deep Neural Network Class Structure
public class DeepNeuralNetwork
{
private int numInput;
private int numHiddenA;
private int numHiddenB;
private int numOutput;
private double[] inputs;
private double[][] iaWeights;
private double[][] abWeights;
private double[][] boWeights;
private double[] aBiases;
private double[] bBiases;
private double[] oBiases;
private double[] aOutputs;
private double[] bOutputs;
private double[] outputs;
private static Random rnd;
public DeepNeuralNetwork(int numInput, int numHiddenA,
int numHiddenB, int numOutput) { . . }
private static double[][] MakeMatrix(int rows, int cols) { . . }
private void InitializeWeights() { . . }
public void SetWeights(double[] weights) { . . }
public double[] ComputeOutputs(double[] xValues) { . . }
private static double HyperTanFunction(double x) { . . }
private static double[] Softmax(double[] oSums) { . . }
}
The two hidden layers and the single output layer each have an array of associated bias values, named aBiases, bBiases, and oBiases respectively. The local outputs for the hidden layers are stored in class-scope arrays named aOutputs and bOutputs. These two arrays could have been defined locally to the ComputeOutputs method.
Most forms of neural networks use some type of randomization during initialization and training. Static class member rnd is used by the demo network to initialize the weights and bias values. The class exposes three public methods: a constructor, method SetWeights and method ComputeOutputs. Private methods MakeMatrix and InitializeWeights are helpers used by the constructor. Private methods HyperTanFunction and Softmax are the activation functions used by method ComputeOutputs.
The Deep Neural Network Constructor
The deep neural network constructor begins by copying its input parameter values to the corresponding class members:
public DeepNeuralNetwork(int numInput, int numHiddenA,
int numHiddenB, int numOutput)
{
this.numInput = numInput;
this.numHiddenA = numHiddenA;
this.numHiddenB = numHiddenB;
this.numOutput = numOutput;
Next, space for the inputs array is allocated:
inputs = new double[numInput];
Then space for the three weights matrices is allocated, using helper method MakeMatrix:
iaWeights = MakeMatrix(numInput, numHiddenA);
abWeights = MakeMatrix(numHiddenA, numHiddenB);
boWeights = MakeMatrix(numHiddenB, numOutput);
Method MakeMatrix is defined as:
private static double[][] MakeMatrix(int rows, int cols)
{
double[][] result = new double[rows][];
for (int r = 0; r < result.Length; ++r)
result[r] = new double[cols];
return result;
}
The constructor allocates space for the three biases arrays:
aBiases = new double[numHiddenA];
bBiases = new double[numHiddenB];
oBiases = new double[numOutput];
Next, the local and final output arrays are allocated:
aOutputs = new double[numHiddenA];
bOutputs = new double[numHiddenB];
outputs = new double[numOutput];
The constructor concludes by instantiating the Random object and then calling helper method InitializeWeights:
rnd = new Random(0);
InitializeWeights();
} // ctor
Method InitializeWeights is defined as:
private void InitializeWeights()
{
int numWeights = (numInput * numHiddenA) + numHiddenA +
(numHiddenA * numHiddenB) + numHiddenB +
(numHiddenB * numOutput) + numOutput;
double[] weights = new double[numWeights];
double lo = -0.01;
double hi = 0.01;
for (int i = 0; i < weights.Length; ++i)
weights[i] = (hi - lo) * rnd.NextDouble() + lo;
this.SetWeights(weights);
}
Method InitializeWeights assigns random values in the interval -0.01 to +0.01 to each weight and bias variable. You might want to pass the interval values in as parameters to InitializeWeights. If you refer back to Listing 1, you'll notice that the Main method calls method SetWeights immediately after the DeepNeuralNetwork constructor is called, which means that initial random weights and bias values are immediately overwritten. However, in a normal, non-demo scenario where SetWeights isn't called in the Main method, initializing weights and bias values is almost always necessary.
Setting the Network Weights
The code for method SetWeights is presented in Listing 3. Method SetWeights accepts an array of values that represent both weights and bias values. The method assumes the values are stored in a particular order: input-to-A weights followed by A-layer biases, followed by A-to-B weights, followed by B-layer biases, followed by B-to-output weights, followed by output biases.
Listing 3: Method SetWeights
public void SetWeights(double[] weights)
{
int numWeights = (numInput * numHiddenA) + numHiddenA +
(numHiddenA * numHiddenB) + numHiddenB +
(numHiddenB * numOutput) + numOutput;
if (weights.Length != numWeights)
throw new Exception("Bad weights length");
int k = 0;
for (int i = 0; i < numInput; ++i)
for (int j = 0; j < numHiddenA; ++j)
iaWeights[i][j] = weights[k++];
for (int i = 0; i < numHiddenA; ++i)
aBiases[i] = weights[k++];
for (int i = 0; i < numHiddenA; ++i)
for (int j = 0; j < numHiddenB; ++j)
abWeights[i][j] = weights[k++];
for (int i = 0; i < numHiddenB; ++i)
bBiases[i] = weights[k++];
for (int i = 0; i < numHiddenB; ++i)
for (int j = 0; j < numOutput; ++j)
boWeights[i][j] = weights[k++];
for (int i = 0; i < numOutput; ++i)
oBiases[i] = weights[k++];
}
Method SetWeights also assumes the weights are stored in row-major form, where the row indices are the "from" indices and to column indices are the "to" indices. For example, if iaWeights[0] [2] = 1.23, then the weight from input node [0] to layer-A node [2] has value 1.23.
An alternative design for method SetWeights is to pass the weights and bias values in as six separate parameters rather than as a single-array parameter. Or you might want to overload SetWeights to accept either a single array parameter or six weights and bias value parameters.
Computing Deep Neural Network Outputs
Merhod ComputeOutputs begins by setting up scratch arrays to hold preliminary (before activation) sums:
public double[] ComputeOutputs(double[] xValues)
{
double[] aSums = new double[numHiddenA];
double[] bSums = new double[numHiddenB];
double[] oSums = new double[numOutput];
These scratch arrays could have been declared as class members; if so, remember to zero out each array at the beginning of ComputeOutputs. Next, the input values are copied into the corresponding class array:
for (int i = 0; i < xValues.Length; ++i)
this.inputs[i] = xValues[i];
An alternative is to use the C# Array.Copy method here. Notice the input values aren't changed by ComputeOutputs, so an alternative design is to eliminate the class member array named inputs, and to eliminate the need to copy values from the xValues array. In my opinion, the explicit inputs array makes a slightly clearer design and is worth the overhead of an extra array copy operation.
The next step is to compute the preliminary sum of weights times inputs for the layer-A nodes, add the bias values, then apply the activation function:
for (int j = 0; j < numHiddenA; ++j) // weights * inputs
aSums[j] += this.inputs[i] * this.iaWeights[i][j];
for (int i = 0; i < numHiddenA; ++i) // add biases
aSums[i] += this.aBiases[i];
for (int i = 0; i < numHiddenA; ++i) // apply activation
this.aOutputs[i] = HyperTanFunction(aSums[i]);
In the demo, I use a WriteLine statement along with helper method ShowVector to display the pre-activation sums and the local layer-A outputs.
Next, the layer-B local outputs are computed, using the just-computed layer-A outputs as local inputs:
for (int j = 0; j < numHiddenB; ++j)
for (int i = 0; i < numHiddenA; ++i)
bSums[j] += aOutputs[i] * this.abWeights[i][j];
for (int i = 0; i < numHiddenB; ++i)
bSums[i] += this.bBiases[i];
for (int i = 0; i < numHiddenB; ++i)
this.bOutputs[i] = HyperTanFunction(bSums[i]);
Next, the final outputs are computed:
for (int j = 0; j < numOutput; ++j)
for (int i = 0; i < numHiddenB; ++i)
oSums[j] += bOutputs[i] * boWeights[i][j];
for (int i = 0; i < numOutput; ++i)
oSums[i] += oBiases[i];
double[] softOut = Softmax(oSums);
Array.Copy(softOut, outputs, softOut.Length);
The final outputs are computed into the class array named outputs. For convenience, these values are also returned by method:
double[] retResult = new double[numOutput];
Array.Copy(this.outputs, retResult, retResult.Length);
return retResult;
}
An alternative to explicitly returning the weights and bias values as an array is to return void and implement a public method GetWeights. Method HyperTanFunction is defined as:
private static double HyperTanFunction(double x)
{
if (x < -20.0) return -1.0; // correct to 30 decimals
else if (x > 20.0) return 1.0;
else return Math.Tanh(x);
}
And method Softmax is defined as:
private static double[] Softmax(double[] oSums)
{
double max = oSums[0];
for (int i = 0; i < oSums.Length; ++i)
if (oSums[i] > max) max = oSums[i];
double scale = 0.0;
for (int i = 0; i < oSums.Length; ++i)
scale += Math.Exp(oSums[i] - max);
double[] result = new double[oSums.Length];
for (int i = 0; i < oSums.Length; ++i)
result[i] = Math.Exp(oSums[i] - max) / scale;
return result; // scaled so xi sum to 1.0
}
Method Softmax is quite subtle, but it's unlikely you'd ever want to modify it, so you can usually safely consider the method a magic black box function.
Go Exploring
The code and explanation presented in this article should give you a good basis for understanding neural networks with two hidden layers. What about three or more hidden layers? The consensus in research literature is that two hidden layers is sufficient for almost all practical problems. But I'm not entirely convinced, and fully connected feed-forward neural networks with more than two hidden layers are relatively unexplored.
Training a deep neural network is much more difficult than training an ordinary neural network with a single layer of hidden nodes, and this factor is the main obstacle to using networks with multiple hidden layers. Standard back-propagation training often fails to give good results. In my opinion, alternate training techniques, in particular particle swarm optimization, are promising. However, these alternatives haven't been studied much.