Neural Network Lab
Neural Network Train-Validate-Test Stopping
The train-validate-test process is hard to sum up in a few words, but trust me that you'll want to know how it's done to avoid the issue of model overfitting when making predictions on new data.
The neural network train-validate-test process is a technique used to reduce model overfitting. The technique is also called early stopping. Although train-validate-test isn't conceptually difficult, the process is a bit difficult to explain because there are several inter-related ideas involved.
A neural network with n input nodes, h hidden nodes, and m output nodes has (n * h) + h + (h * m) + m weights and biases. For example, a network with 4 input nodes, 5 hidden nodes, and 3 output nodes has (4 * 5) + 5 + (5 * 3) + 3 = 43 weights and biases. These are numeric constants that must be determined.
Training a neural network is the process of finding the values for the weights and biases. In most scenarios, training is accomplished using what can be described as a train-test technique. The available data, which has known input and output values, is split into a training set (typically 80 percent of the data) and a test set (the remaining 20 percent).
The training data set is used to train the neural network. Various values of the weights and biases are checked to find the set of values so that the computed output values most closely match the known, correct output values. Or, put slightly differently, training is the process of finding values for the weights and biases so that error is minimized. There are many training algorithms, notably back-propagation, and particle swarm optimization.
During training, the test data is not used at all. After training completes, the accuracy of the resulting neural network model's weights and biases are applied just once to the test data. The accuracy of the model on the test data gives you a very rough estimate of how accurate the model will be when presented with new, previously unseen data.
One of the major challenges when working with neural networks is a phenomenon called overfitting. Model overfitting occurs when the training algorithm runs too long. The result is a set of values for the weights and biases that generate outputs that almost perfectly match the training data, but when those weights and bias values are used to make predictions on new data, the model has very poor accuracy.
The train-validate-test process is designed to help identify when model overfitting starts to occur, so that training can be stopped. Instead of splitting the available data into two sets, train and test, the data is split into three sets: a training set (typically 60 percent of the data), a validation set (20 percent) and a test set (20 percent).
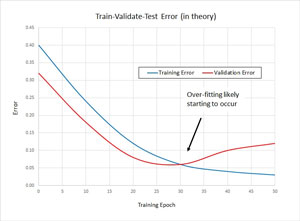
Take a look at the graph in Figure 1. Training uses the training data as usual. However, every now and then (typically once every 10 or 100 training epochs/iterations), the error associated with the current values of the weights and biases is calculated. In many situations, the longer you apply the training algorithm, the lower the error will be on the training set. In fact, it's often possible to eventually generate values for the weights and biases so that the error on the training set is almost zero, which will almost certainly lead to model overfitting.
 [Click on image for larger view.]
Figure 1. Training and Validation Error
[Click on image for larger view.]
Figure 1. Training and Validation Error
But when the current values of the weights and biases are applied to the validation data set, at some point the error will likely start to increase. For example, in Figure 1, the error on the validation data begins to increase at approximately epoch 30. This means you should stop training at epoch 30 and use the values of the weight and biases at that epoch.
The test data set is used as normal: After the model weights and bias value have been determined, they are applied to the test data, and the resulting accuracy is an estimate of the overall accuracy of the neural network model.
A Demo Program
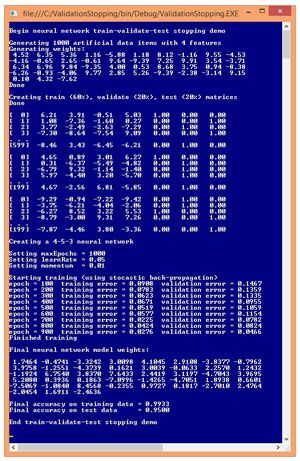
A good way to get a feel for exactly what the neural network train-validate-test process is and to see where this article is headed, is to examine the screenshot of a demo program in Figure 2. The demo begins by generating a 1,000-item synthetic data set. The synthetic data has four input values, each of which is between -10.0 and +10.0, and three output values that correspond to 1-of-N encoded data, for example (0, 1, 0) such as a scenario where the values to predict are "republican." "democrat," and "other."
 [Click on image for larger view.]
Figure 2. Train-Validate-Test Demo Program
[Click on image for larger view.]
Figure 2. Train-Validate-Test Demo Program
The synthetic data is randomly split into a 600-item training set, a 200-item validation set and a 200-item test set. A weakness of the train-validate-test process, compared to the normal train-test approach, is that you must have a lot of data. Next, a 4-5-3 neural network is created. The number of hidden nodes, 5, was arbitrary and in realistic scenarios you must typically experiment to find a good number of hidden nodes.
The demo neural network is trained using standard back propagation with a learning rate set to 0.05 and momentum factor set to 0.01. Again, in a realistic scenario you'd have to experiment to get good values for these parameters.
As training progresses, the demo program displays errors associated with the values of the current weights and biases, every 100 epochs. Notice that the error on the training set and on the validation set doesn't behave like the idealized graph in Figure 1. Instead, the error values jump around a bit. Interpreting exactly when validation error starts to increase (and when to stop training) is often difficult, and is as much art as it is science.
The demo concludes by displaying the values of the 43 weights and biases, and the neural network's accuracy on the training data (99.33 percent) and on the test data (95.00 percent). The accuracy on the test data is the most relevant value, and is an estimate of the accuracy you could expect if the model was presented with new data that has unknown output values.
The demo program is coded using C#, but you shouldn't have much trouble if you want to refactor to another language such as VB.NET or Python. The demo program is too long to present in its entirety, but the complete source code is available in the code download that accompanies this article. All normal error checking has been removed to keep the main ideas as clear as possible.
The remainder of this article assumes you have at least intermediate-level programming skills with a C-family language, and a solid grasp of basic neural network concepts, but doesn't assume you know anything about train-validate-test stopping.
Demo Program Structure
The overall structure of the demo program, with a few minor edits to save space, is presented in Listing 1. To create the demo, I launched Visual Studio and created a new C# console application named ValidationStopping. After the template code loaded, in the Solution Explorer window, I renamed file Program.cs to ValidateStopProgram.cs and then Visual Studio automatically renamed class Program for me.
The demo program has no significant .NET dependencies so any version of Visual Studio should work. In the editor window, at the top of template-generated code, I deleted all unnecessary using statements, leaving just the reference to the top-level System namespace.
Listing 1: ValidationStopping Program Structure
using System;
namespace ValidationStopping
{
class ValidateStopProgram
{
static void Main(string[] args)
{
Console.WriteLine("Begin train-validate-test demo");
// Program statements here
Console.WriteLine("End train-validate-test demo");
Console.ReadLine();
} // Main
public static void ShowMatrix(double[][] matrix,
int numRows, int decimals, bool indices) { . . }
public static void ShowVector(double[] vector,
static double[][] MakeAllData(int numInput,
int numHidden, int numOutput,
int numRows, int seed) { . . }
static void Split(double[][] allData, double trainPct,
int seed, out double[][] trainData,
out double[][] validateData,
out double[][] testData) { . . }
} // Program
public class NeuralNetwork
{
private int numInput;
private int numHidden;
private int numOutput;
private double[] inputs;
private double[][] ihWeights;
private double[] hBiases;
private double[] hOutputs;
private double[][] hoWeights;
private double[] oBiases;
private double[] outputs;
private Random rnd;
public NeuralNetwork(int numInput, int numHidden,
int numOutput) { . . }
private static double[][] MakeMatrix(int rows,
int cols, double v) { . . }
private void InitializeWeights() { . . }
public void SetWeights(double[] weights) { . . }
public double[] GetWeights() { . . }
public double[] ComputeOutputs(double[] xValues) { . . }
private static double HyperTan(double x) { . . }
private static double[] Softmax(double[] oSums) { . . }
public double[] Train(double[][] trainData,
double[][] validateData, int maxEpochs,
double learnRate, double momentum) { . . }
private void Shuffle(int[] sequence) { . . }
private double Error(double[][] data) { . . }
public double Accuracy(double[][] data) { . . }
private static int MaxIndex(double[] vector) { . . }
} // NeuralNetwork
} // ns
All the program control logic is housed in the Main method. Helper methods ShowVector and ShowMatrix display an array- or an array-of-arrays-style matrix to the shell. Helper method MakeAllData generates the source synthetic data set. Helper method Split accepts a source data set in a matrix, a returns as out-parameters, three matrices, holding a training set, a validation set and a test set. Method Split accepts a percentage of the source data to use for the training data (typically 0.60), and then allots the validation and test data evenly from the remainder. You might want to parametrize all three percentages.
All neural network functionality is contained in a program-defined NeuralNetwork class. The class exposes six standard methods. A single constructor is defined. Methods SetWeights and GetWeights should be self-explanatory. Method ComputeOutputs isn't called in the Main, but is declared public because the method is needed if making a prediction on new data. Method Train implements the back-propagation algorithm. Method accuracy computes the model accuracy using the current neural network weights and biases. You might want to pass the weights and biases, serialized in an array, to method Accuracy.
Notice that all of the class methods have standard interfaces except for method Train. Instead of requiring just the training data, Train also requires a reference to the validation data set.
The Training and Error Methods
Compared to regular neural network training, when using the train-validate-test approach the two key, related methods are the training method and the error method. The definition of method Train begins:
public double[] Train(double[][] trainData, double[][] validateData,
int maxEpochs, double learnRate, double momentum)
{
double[][] hoGrads = MakeMatrix(numHidden, numOutput, 0.0);
double[] obGrads = new double[numOutput];
double[][] ihGrads = MakeMatrix(numInput, numHidden, 0.0);
double[] hbGrads = new double[numHidden];
...
A neural network training method always requires some sort of reference, explicit as here, or implicit, to the training data. The training method usually requires algorithm-specific information, such as the learning rate and momentum factor when using the back-propagation algorithm, or the number of particles when using particle swarm optimization. When using the train-validate-stop technique, you add an additional reference, to the validation data.
After setting up storage for the hidden-to-output weight gradients (hoGrads), output node bias gradients, input-to-hidden weight gradients, and hidden node bias gradients, method Train continues with:
double[] oSignals = new double[numOutput];
double[] hSignals = new double[numHidden];
double[][] ihPrevWeightsDelta = MakeMatrix(numInput, numHidden, 0.0);
double[] hPrevBiasesDelta = new double[numHidden];
double[][] hoPrevWeightsDelta = MakeMatrix(numHidden, numOutput, 0.0);
double[] oPrevBiasesDelta = new double[numOutput];
Local arrays oSignals and hSignals hold intermediate values used by the back-propagation algorithm. The other two matrices and two arrays hold information needed by the optional, but very common, momentum calculation. Next, the main training loop is prepared:
int epoch = 0;
double[] xValues = new double[numInput];
double[] tValues = new double[numOutput];
int[] sequence = new int[trainData.Length];
for (int i = 0; i < sequence.Length; ++i)
sequence[i] = i;
The local variable named epoch is the loop counter variable. Arrays xValues and tValues hold the input value and the target output values from a training data item. The array named sequence holds the indices of each training item. This array will be shuffled so that on each iteration of the training loop, the training data will be processed in a different, random order.
The main loop begins like so:
int errInterval = maxEpochs / 10;
while (epoch < maxEpochs)
{
++epoch;
...
Variable errInterval establishes how often the error on the validation set will be computed and displayed. Here because maxEpochs was set to 1,000, validation error will be calculated every 100 epochs. Next, the key part of the train-validate-test process occurs:
if (epoch % errInterval == 0 && epoch < maxEpochs)
{
double trainErr = Error(trainData);
double validateErr = Error(validateData);
Console.WriteLine("epoch = " + epoch + " training error = " +
trainErr.ToString("F4") +
" validation error = " + validateErr.ToString("F4"));
// Console.ReadLine();
}
The error on the training and validation data is calculated using the current weights and bias values. These error values are simply displayed to the shell. You might think at first, as I did, that instead of merely displaying the validation error and relying on guesswork to determine when the error level has started to rise, it'd be better to programmatically determine when to stop training. However, because the error will fluctuate, programmatically determining when to stop training is an extremely difficult problem. At least among my colleagues and me, we find it more effective to use the eyeball technique.
After displaying the validation error, method Train proceeds as usual:
...
// Shuffle sequence array
// for-each training item
// Compute gradients and update weights and biases
// end-for
} // while
double[] bestWts = this.GetWeights();
return bestWts;
} // Train
The error method calculates the mean squared error (MSE), which is perhaps best explained by example. Suppose the target values for one item in the training data set are (0, 1, 0). If the computed output values are (0.10, 0.70, 0.20), then the squared error for the data item is (0 - 0.10)^2 + (1 - 0.70)^2 + (0 - 0.20)^2 = 0.01 + 0.09 + 0.04 = 0.14. The MSE is the average of the squared errors for all data items in the training set.
The definition of the error method is presented in Listing 2. The method is defined using private scope because it's called only by method Train. You might want to change the scope to public so that Error can be called outside the NeuralNetwork class definition. If you intend to use the Error method in this way, you'd likely want to refactor the calling signature to include an array of serialized weights and bias values.
Listing 2: The Error Method
private double Error(double[][] data)
{
// Average squared error per training item
double sumSquaredError = 0.0;
double[] xValues = new double[numInput];
double[] tValues = new double[numOutput];
// Examine each data item
for (int i = 0; i < data.Length; ++i)
{
Array.Copy(data [i], xValues, numInput);
Array.Copy(data [i], numInput, tValues, 0, numOutput);
double[] yValues = this.ComputeOutputs(xValues);
for (int j = 0; j < numOutput; ++j)
{
double err = tValues[j] - yValues[j];
sumSquaredError += err * err;
}
}
return sumSquaredError / data.Length;
}
The back-propagation training algorithm assumes the error term to minimize is MSE (well, actually, a slight variation of MSE), even though b-p doesn't explicitly call the error method. So, an option for you to consider is to use the primary alternative to MSE, cross entropy error. To the best of my knowledge, this approach has not been deeply explored by machine learning researchers.
Wrapping Up
The train-validate-test approach is used to limit neural network model overfitting. As usual in machine learning, there's no completely standard terminology. In this article, the data used to determine when to stop training is called the validation data, and the data used to estimate final model accuracy is called the test data. In some research literature, the meanings of the terms validation data and test data are reversed.
There are several other techniques used to limit overfitting. These techniques include hidden node drop-out, weight decay (also called weight regularization), weight restriction, input data jittering, and others. With so many different techniques available, it becomes quite difficult to know which techniques to use, either alone or in combination with other techniques. Research suggests that no one particular technique is the best way to deal with overfitting, and that trial and error is required for a particular problem.