Neural Network Lab
Parameter Sweeps, or How I Took My Neural Network for a Test Drive
The short definition of a parameter sweep is that it's the process of trying different training parameter values in order to find a good set of neural network weight values.
One way to think of a neural network is as a complicated math function that can make predictions. A neural network accepts numeric input values and emits numeric output values. For example, a neural network could accept inputs representing a person's age, sex (where male is -1 and female is +1), and years of education, then generate output values indicating the person's predicted political inclination (where conservative is 1, 0, 0 and moderate is 0, 1, 0 and liberal is 0, 0, 1).
The neural network output values are calculated using a set of numeric constants called weights and biases. Because biases are just special kinds of weights, weights and biases are often collectively referred to as weights when the meaning is clear.
The values of a neural network's weights are determined by using a set of training data that has known input values and known, correct output values. Different values for the weights are tried in order to find a set of weight values that produce calculated output values that are very close to the known correct output values in the training data. After the values of the weights have been determined, they can be used to predict output values when presented with new data.
The process of finding a neural network's weight values is called training the network. There are several different algorithms that can be used for neural network training. By far the most common is called the back-propagation algorithm. Back-propagation requires two mandatory user-supplied parameter values, the maximum number of training iterations and the learning rate.
Back-propagation typically requires two additional, optional parameter values, the momentum rate and the decay rate. In simplified terms, the learning rate parameter controls how quickly weight values change during training. The momentum rate parameter controls how quickly weight values adjust when they overshoot good values. The weight decay parameter throttles weight values during training so that they don't increase toward positive infinity.
As it turns out, the neural network weight values that are produced by back-propagation training are often very sensitive to the values of the four training parameters. For example, if you use a learning rate value of 0.01 you might get neural network weight values that produce a highly inaccurate model, but a slight change to the learning rate, say to 0.02, could easily produce a very good model.
Because training is so sensitive to the four training parameter values, neural network training is a matter of trial and error to some extent. The process of trying different training parameter values in order to find a good set of neural network weight values, is called a parameter sweep.
A Parameter Sweep in Action
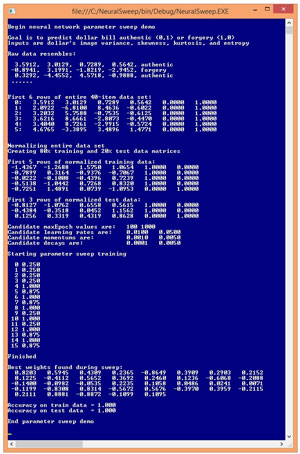
A good way to understand neural network parameter sweeps, and to see where this article is headed, is to examine the screenshot of the demo program in Figure 1. The goal of the demo neural network is to predict whether a banknote (think dollar bill) is authentic or a forgery. There are four input values (often called features in machine language terminology). You don't have to understand the meaning of the input variables.
 [Click on image for larger view.]
Figure 1. Parameter Sweeps Demo Program
[Click on image for larger view.]
Figure 1. Parameter Sweeps Demo Program
The demo uses a 40-item data set that has 20 authentic banknotes and 20 forgeries. The demo data is a subset of a real 1,372-item data set called the UCI banknote authentication data set. The demo program encodes authentic as (0, 1) and forgery as (1, 0). An alternative to this two-output-node technique would be to use a single output node and encode authentic as 0 and forgery as 1.
The demo program normalizes the input data values. For this problem, normalization isn't necessary because the four input values all have roughly the same magnitude so no single input variable will dominate the others.
The demo program randomly splits the 40-item normalized data set into a 32-item training set (80 percent of the data), which is used to determine the neural network weights, and an eight-item test set, which is used to evaluate the accuracy of the resulting neural network model.
The demo program sets up candidate values for the four training parameters. The values for the maximum number of epochs are 100 and 1,000. The values for the learning rate are 0.01 and 0.05. The values for the momentum rate are 0.001 and 0.005. The values for the weight decay rates are 0.0001 and 0.005.
Because there are two maximum epoch values, two learning rate values, two momentum rate values, and two weight decay rate values, there are a total of 2 * 2 * 2 * 2 = 16 possible combinations of the four parameter values. The first set of values would be (100, 0.01, 0.001, 0.0001). The second set of values would be (100, 0.01, 0.001, 0.005) and the 16th (last) set of parameter values would be (1000, 0.05, 0.005, 0.005).
Behind the scenes, the demo program trains a 4-input, 5-hidden, 2-output neural network using back-propagation with each of the 16 possible sets of parameter values. The demo program displays the resulting accuracy of the generated neural network on the test data for each of the 16 parameter sets.
The first four sets of parameter values produce a very poor neural network that has only 25 percent accuracy -- because the goal is to predict authentic or forgery, you could do much better by guessing randomly! Parameter sets number 4 through 8 produce very good models that have accuracy of either 87.5 percent (seven out of eight correct predictions on the test data) or 100 percent.
A fully connected neural network that has x input nodes, h hidden nodes, and y output nodes has (x * h) + h + (h * y) + y weights and biases. So the 4-5-2 demo neural network has (4 * 5) + 5 + (5 * 2) + 2 = 37 weights and biases. The demo program concludes by displaying the 37 weights and bias values that correspond to the best neural network found during training.
The Demo Program
To create the demo program I launched Visual Studio and selected the C# console application project template. I named the project NeuralSweep. The demo has no significant Microsoft .NET Framework dependencies so any version of Visual Studio will work. After the template code loaded, in the Solution Explorer window I right-clicked on file Program.cs and renamed it to the more descriptive NeuralSweepProgram.cs and then allowed Visual Studio to automatically rename class Program. At the top of the template-generated code in the Editor window, I deleted all unnecessary using statements, leaving just the reference to the top-level System namespace.
The overall structure of the demo program is shown in Listing 1. Helper method Normalize performs a z-score normalization on the banknote data. Method Split creates a reference copy of the source data and splits it into a training set and a test set. All of the neural network logic is contained in a program-defined NeuralNetwork class. Method Sweep iterates through each of the 16 possible combinations of training parameter values, creates and trains a 4-5-2 neural network and returns the best weights and biases values found.
Listing 1: Demo Program Structure
using System;
namespace NeuralSweep
{
class NeuralSweepProgram
{
static void Main(string[] args)
{
Console.WriteLine("Begin parameter sweep demo");
// All control statements here
Console.WriteLine("End parameter sweep demo");
}
static double[] Sweep(int numInput, int numHidden,
int numOutput, int seed,
double[][] trainData, double[][] testData,
int[] maxEpochs, double[] learnRates,
double[] momentums, double[] decays) { . . }
static void Normalize(double[][] dataMatrix,
int[] cols) { . . }
static void Split(double[][] allData,
double trainPct, int seed,
out double[][] trainData,
out double[][] testData) { . . }
static void ShowVector(double[] vector,
int valsPerRow, int decimals, bool newLine) { . . }
static void ShowVector(int[] vector, int valsPerRow,
bool newLine) { . . }
static void ShowMatrix(double[][] matrix, int numRows,
int decimals, bool lineNums, bool newLine) { . . }
} // Program class
public class NeuralNetwork { . . }
} // ns
After some preliminary WriteLine statements, the Main method sets up the 40-item source data with these statements:
double[][] allData = new double[40][];
allData[0] = new double[] { 3.5912, 3.0129, 0.7289, 0.5642, 0, 1 };
allData[1] = new double[] { 2.0922, -6.8100, 8.4636, -0.6022, 0, 1 };
. .
allData[39] = new double[] { -1.6677, -7.1535, 7.8929, 0.9677, 1, 0 };
Console.WriteLine("First 6 rows of entire 40-item data set:");
ShowMatrix(allData, 6, 4, true, true);
In most situations you would read source data from a text file using a program-defined method named something like LoadData. Next, the source data is normalized:
Console.WriteLine("Normalizing entire data set");
Normalize(allData, new int[] { 0, 1, 2, 3 });
The Normalize method accepts an array of 0-based columns to normalize. Notice that the last two columns, 4 and 5, are not normalized because they hold the encoded output values of (1, 0) or (0, 1).
The source data is split into training and test sets, like so:
double[][] trainData = null;
double[][] testData = null;
double trainPct = 0.80;
int splitSeed = 0;
Split(allData, trainPct, splitSeed,
out trainData, out testData);
The choice of the seed value (0) for the random number generator used in Split was arbitrary. Next, the parameter sweep values are created with these statements:
int[] maxEpochs = new int[] { 100, 1000 };
double[] learnRates = new double[] { 0.01, 0.05 };
double[] momentums = new double[] { 0.001, 0.005 };
double[] decays = new double[] { 0.0001, 0.005 };
Unfortunately, there aren't really any good guidelines or general rules of thumb for parameter values and so you must rely on a bit of experimentation. In many situations you should consider including 0.0 values for the optional momentum rates and weight decay rates.
The parameter sweep is performed by these statements:
Console.WriteLine("Starting parameter sweep");
double[] finalWts = Sweep(numInput, numHidden, numOutput,
seed, trainData, testData,
maxEpochs, learnRates, momentums, decays);
Console.WriteLine("Finished");
Console.WriteLine("Best weights found during sweep:");
ShowVector(finalWts, 8, 4, true);
A significant design alternative is to consider the number of hidden nodes as an additional parameter. The number of input and output nodes is determined by the particular problem and data you have. But the number of hidden nodes can vary and significantly affects neural network behavior. On the other hand, the choice of hidden node internal activation function (typically hyperbolic tangent or logistic sigmoid) has little impact, at least based on my experience.
The demo program concludes by evaluating the accuracy of the neural network model created by the parameter sweep training:
NeuralNetwork nn = new NeuralNetwork(numInput, numHidden,
numOutput, seed);
nn.SetWeights(finalWts);
double trainAcc = nn.Accuracy(trainData);
double testAcc = nn.Accuracy(testData);
Console.WriteLine("Accuracy on train data = " +
trainAcc.ToString("F3"));
Console.WriteLine("Accuracy on test data = " +
testAcc.ToString("F3"));
Of the two accuracy values, the accuracy of the neural network on the test data is more important than the accuracy on the training data. The test data accuracy gives you a very rough estimate of how accurate the neural network will be when presented with new data that has unknown output values. The main use of the training accuracy value is to check that it isn't significantly different from the test accuracy, which would indicate something is likely wrong with your model.
Analyzing Parameter Sweeps
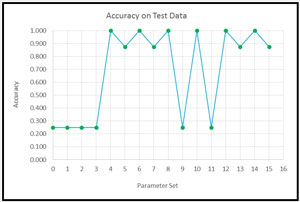
My preferred technique for analyzing parameter sweep information is to create a graph like the one shown in Figure 2. The graph shows the accuracy of the demo neural network for each of the 16 sets of training parameter values.
 [Click on image for larger view.]
Figure 2. Graphing Parameter Sweep Information
[Click on image for larger view.]
Figure 2. Graphing Parameter Sweep Information
By visually examining a parameter sweep information graph you can often spot patterns that would be very difficult to find programmatically. For example, you can often identify specific learning rate or momentum rate values that have a very large effect on predictive accuracy. Also, it's sometimes possible to see ranges of promising parameter values that merit additional investigation.
The Sweep Method
The definition of method Sweep starts with:
static double[] Sweep(int numInput, int numHidden, int numOutput,
int seed, double[][] trainData, double[][] testData,
int[] maxEpochs, double[] learnRates,
double[] momentums, double[] decays)
{
int numWts = (numInput * numHidden) +
(numHidden * numOutput) + numHidden + numOutput;
double[] bestWts = new double[numWts];
...
The method accepts a large number of parameters. An alternative design is to encapsulate the candidate parameter sweep values into a class, but in my opinion the advantage gained by that approach isn't worth the added effort. Next, local variables to hold the best values found during the sweep are set up:
double bestAcc = 0.0;
int bestMaxEpochs;
double bestLearnRate;
double bestMomentum;
double bestDecay;
Because accuracy can only be positive or zero, initializing the best accuracy to 0.0 will guarantee that any accuracy found will be better as long as at least one set of training parameters has accuracy greater than zero.
The core statements of method Sweep iterate through all combinations of the candidate training parameter values like so:
int paramSet = 0;
foreach (int me in maxEpochs) {
foreach (double lr in learnRates) {
foreach (double mo in momentums) {
foreach (double de in decays) {
// Create, train, save if better
} // Decay
} // Momentum
} // LearnRate
} // MaxEpoch
In general, I'm not a big fan of the foreach statement and prefer using the humble for statement with index variables, but in this situation I think the foreach approach is clearly simpler and less error-prone.
Inside the four deeply nested loops, a neural network is instantiated and trained like this:
NeuralNetwork nn = new NeuralNetwork(numInput, numHidden,
numOutput, seed);
double[] wts = nn.Train(trainData, me, lr, mo, de, false);
double currAcc = nn.Accuracy(testData);
The trailing false argument passed to method Train indicates not to display progress messages. The demo program displays the error associated with each set of training parameter values:
Console.WriteLine(paramSet.ToString().PadLeft(3) + " " +
currAcc.ToString("F3"));
++paramSet;
As discussed in the previous section, it's usually a good idea to display sweep error so you can identify patterns. After training with the current set of parameter values, the neural network is evaluated and if a better model is found, the associated weights and bias values are saved:
if (currAcc > bestAcc) { // new best
for (int p = 0; p < numWts; ++p)
bestWts[p] = wts[p]; // save weights
bestMaxEpochs = me; bestLearnRate = lr;
bestMomentum = mo; bestDecay = de;
bestAcc = currAcc;
}
The definition of method Sweep finishes by returning the best weights found:
...
return bestWts;
} // Sweep
Method Sweep returns just the best neural network weight values found. You might want to also return, as out parameters, the training parameter values that generated the best weights.
Wrapping Up
There are some alternative neural network training parameter sweep approaches to the one outlined in this article. Instead of setting up arrays of candidate values, you can set up two endpoints for each parameter and then randomly generate values. For example, for the learning rate, you could set a minimum value of 0.0001 and a maximum value of 0.10 and then select a random value between the minimum and maximum values.
A more sophisticated alternative approach is to use a genetic algorithm to find good training parameter values. This requires quite a bit of effort but there are some research results that suggest using a genetic algorithm is very effective for producing high-accuracy neural networks.