In-Depth
Functional Programming, the .NET Way
The functional programming paradigm, which has been around for decades, has never gone out of style. In this two-part series, we look at Microsoft's implementation, Visual F#.
- By Arnaldo Pérez Castaño
- 02/10/2016
Also See:
When developing applications, programmers must follow certain rules linked to the programming languages implicated in the developing process. These rules are not only syntactical or semantic but also "philosophical," related to the programming paradigms adopted by the language at hand.
A programming paradigm represents a philosophy, a set of ideas and concepts used as guide to develop software; usually centered on some element which represents the main piece of its philosophy. Some of the oldest programming paradigms are the object-oriented programming centered on "objects" (1970s), procedural programming centered on procedures (1950s), and functional programming centered on functions (1950s).
Much like we have architectural movements for building houses where each one is related to certain styles (high ceiling, big columns, etc.), in programming we have different programming paradigms to build computer programs according to the "styles" defined in the paradigm. As it occurs in architecture when building a house, building a computer program can mix several "styles" from different paradigms.
Even though object-oriented programming remains popular today, the vigorous development of functional programming during the last decades and the acceptance of many of its positive features (clean, compact, legible code, etc.) have contributed to the inclusion of such features in popular multi-paradigm languages like C# and Python. With the release of Visual Studio 2010, the Visual F# functional language officially shipped; it now constitutes the alternative offered by Microsoft for functional programming on the .NET platform.
Let's look at some of the characteristics and benefits of functional programming through different examples developed in F#. Here, I'll describe some of the language's features and how you could take advantage of these features in your applications.
Features of Functional Paradigm Languages
Some of the features of functional programming are:
-
Everything moves around functions: They are treated as data and considered as pure mathematical functions.
- No side effects: Data is not allowed to change over program execution. In a procedure the value of a variable could change causing unexpected results from other procedures using the same variable. In the functional paradigm, functions are purely mathematical and they cannot change the value of an identifier.
- Syntactic amenities can be used for creating, manipulating and composing functions.
- Direct syntactic statements can be used for creating data types like lists, sequences, etc.
- Functional paradigm allows for pattern matching.
- Recursion, iteration is accomplished through recursion.
- Lazy evaluation -- an expression is evaluated only when required.
- Functional programming has more expressive, legible and elegant code.
- The basis for functional programming has its basis in lambda calculus.
Lambda calculus is a mathematical theory originated in the 1930s by Alonzo Church which provides an abstraction from the common notation and evaluation of functions to a more simplified and practical notation and evaluation. Using the traditional notation we would write a function like this:
f(x) = x + 2
then evaluate it in the following manner:
f(3) = 3 + 2 = 5
Since Church's theory relies heavily on functions, he introduced a notation that allowed a function to be written without specifying a name. Thus the previous function in lambda calculus would be written as:
(λx.x+2)
and evaluate it as
(λx.x+2) 3 = 3 + 2 = 5
The lambda function takes a single parameter, denoted by the Greek letter lambda followed by the variable name x. The declaration of the parameters is followed by a dot and by the body of the function, in this case x+2. The evaluation of the function is accomplished by writing the function followed by the argument.
There are two key elements of lambda calculus that make it the keystone of functional programming:
- Everything is considered or defined as a function (operators, numerals, etc.).
- Any function can take another function as argument.
As we'll see shortly, lambda functions are usually known as anonymous functions, a very common feature in functional programming. We'll examine this and other points in detail in the next sections.
F# and .NET Platform
The set of functional languages is divided into two main categories: the pure functional languages and the hybrid languages. The first applies strictly to all features previously mentioned, maintaining maximum legibility and a highly expressive code. The latter being more relaxed, allows several concepts from procedural languages (variable assignation, for loops, etc.). F# belongs to the second class -- it's a hybrid functional language.
As a hybrid F# doesn't impose the use of immutable data types, though their use is recommended. In F# you can define a mutable value and work with .NET objects; a necessary feature in view of the fact that allows .NET functionality and libraries (usually not related to the functional paradigm) to be accessible from within the language.
Ultimately, F# remains primarily as a functional language which implies that it converges to most features of the functional paradigm and considers them as significant when developing an F# program. From now on we'll describe some of the most important elements of functional programming in F#.
Syntactic Sugar
Before we begin our immersion into F# let's provide some insight on the language's syntax. We need to lay this ground as we'll start seeing F# code from now and up to the end of this article.
F# follows the principles of functional programming, and it uses identifiers instead of variables. An identifier is declared using the let keyword followed by the name of the identifier, an equal sign and some expression returning a value. In the next code we see how the 4 value is assigned to identifier x:
let x= 4
What's the difference between a variable and an identifier?
While we can change the value of a variable (mutable), we cannot change the value of an identifier. This is how it should be in pure functional languages, but F# is not pure so under certain circumstances you can redefine the value of an identifier.
An identifier can also hold a function:
let f x = x + 2
To obtain its value we use an expression consisting of the function's name followed by its arguments:
(f 3)
In order to test our examples we set up the next F# application:
open System
[<EntryPoint>>]
let main argv =
let x = 4
let f x = x + 2
printfn "%d" (f 3)
// Read user input
let input = Console.ReadLine()
0 // return an integer exit code
Notice how we are using objects and methods from .NET (Console.ReadLine). F# is connected to the platform so we can operate with all of its components. The "open System" expression on the first line is equivalent to the "using System" that we would write in C# -- it's just to import some library. We structure code in F# following indentation levels; that's how the language recognizes the program's logic.
As I mentioned it's possible to consider functions as values and it's also possible to create inner functions. In the next code function f(x) = x^2 + 2 is computed by first obtaining the value of the inner function g(x) = x^2 and then adding 2 to the prior result:
let f x =
let g y = y ** 2.0
(g x) + 2.0
The ** operator corresponds to the exponentiation operation; it receives float type arguments.
Function composition could be easily obtained in F#. If we have f(x) = x^2 and g(x) = x + 1 then f (g(x)) = g (x) ^ 2 could be obtained as follows:
let f x = x ** 2.0
let g x = x + 1.0
let composition x = f (g x)
Now let's see how we can declare lists on F#:
// Empty List
let l1 = []
// List with elements 1, 2, 3
let l2 = [1; 2; 3]
// Concatenate an element with a list
let l3 = 1 :: [2; 3]
// Concatenate lists
let l4 = [1; 2] @ [3; 4]
// Ranged list
let l5 = [1 .. 10]
// Generated list
let l6 = [for x in 1..5 -> x * 2]
After printing every list the results would be the following:
printfn "&A" 11
printfn "&A" 12
printfn "&A" 13
printfn "&A" 14
printfn "&A" 15
printfn "&A" 16
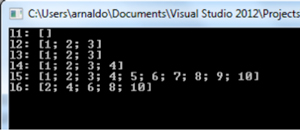
Results are shown in Figure 1.
 [Click on image for larger view.]
Figure 1: Results of the F# Declared List
[Click on image for larger view.]
Figure 1: Results of the F# Declared List
A description of each list declaration is presented next:
- l1: empty list declared using square brackets ([ ]).
- l2: list containing 3 elements.
- l3: list declared by concatenating a single element with another list using the concatenation operator (::).
- l4: list declared by concatenating 2 other lists using the list concatenation operator (@).
- l5: list declared by creating a ranged list; it will contained every element on the defined range, in this case [1; 2; 3; 4; 5; 6; 7; 8; 9; 10].
- l6: list declared by creating a generated list; it will contained every element that results from the application of the expression to the right of the -> operator. The expression is applied to every element in the collection declared to the left of the operator; hence the resulting list has as many elements as elements in the specified range.
Both lists l5, l6 are representatives of syntax construct known as List Comprehension which facilitates the creation of lists in two forms: ranged list and generated list.
Sequences could be declared using one of the following syntaxes:
let s1 = seq [1; 2]
let s2 = {1..10}
let s3 = seq {for x in {1..5} -> x * 2}
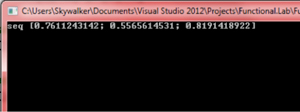
The main advantage with sequences is that they provide lazy evaluation (evaluation of elements only when required) -- hence, you could have an infinite sequence. This scenario is shown in the next code where we create an infinite sequence of random numbers in the range [0, 1]:
let randomseq =
seq {
let r = new Random()
while true do yield r.NextDouble()
}
printfn "%A" (Seq.take 3 randomseq)
The result is shown in Figure 2.
 [Click on image for larger view.]
Figure 2: Generated Random Number Sequence
[Click on image for larger view.]
Figure 2: Generated Random Number Sequence
In the previous code we used .NET objects and object-oriented notation (Random object, new keyword, dot notation) and we used a well known procedural statement, with the while statement showing us some of the hybrid alternatives of the language.
The take function represents a higher order function. We won't get into details in this topic as it will be explained at some other time. In short, so that you understand the previous code, know that a higher order function is one that takes another function as argument. In this case the take function takes the first three elements from the randomseq collection.
That's a lot to digest, I know. Next time, we look at a range of functions you can write, pattern matching, and other features of F#.
About the Author
Arnaldo Perez Castano is a computer scientist based in Cuba. He is the author of a series of programming books -- JavaScript Facil, HTML y CSS Facil, and Python Facil (Marcombo S.A). His expertise includes Visual Basic, C#, .NET Framework, and artificial intelligence, and offers his services as a freelancer through nubelo.com. Cinema and music are some of his passions. Contact him at [email protected].