The Data Science Lab
Neural Regression Using PyTorch: Training
The goal of a regression problem is to predict a single numeric value, for example, predicting the annual revenue of a new restaurant based on variables such as menu prices, number of tables, location and so on.
The goal of a regression problem is to predict a single numeric value, for example, predicting the annual revenue of a new restaurant based on variables such as menu prices, number of tables, location and so on. There are several classical statistics techniques for regression problems. Neural regression solves a regression problem using a neural network. This article is the third in a series of four articles that present a complete end-to-end production-quality example of neural regression using PyTorch. The recurring example problem is to predict the price of a house based on its area in square feet, air conditioning (yes or no), style ("art_deco," "bungalow," "colonial") and local school ("johnson," "kennedy," "lincoln").
The process of creating a PyTorch neural network for regression consists of six steps:
- Prepare the training and test data
- Implement a Dataset object to serve up the data in batches
- Design and implement a neural network
- Write code to train the network
- Write code to evaluate the model (the trained network)
- Write code to save and use the model to make predictions for new, previously unseen data
Each of the six steps is complicated. And the six steps are tightly coupled which adds to the difficulty. This article covers the fourth step -- training a neural network for neural regression.
A good way to see where this series of articles is headed is to take a look at the screenshot of the demo program in Figure 1. The demo begins by creating Dataset and DataLoader objects which have been designed to work with the house data. Next, the demo creates an 8-(10-10)-1 deep neural network. The demo prepares training by setting up a loss function (mean squared error), a training optimizer function (Adam) and parameters for training (learning rate and max epochs).
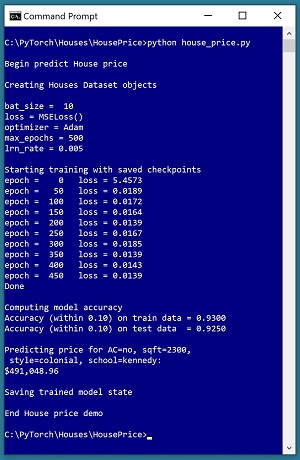 [Click on image for larger view.] Figure 1: Predicting the Price of a House Using Neural Regression
[Click on image for larger view.] Figure 1: Predicting the Price of a House Using Neural Regression
The demo trains the neural network for 500 epochs in batches of 10 items. An epoch is one complete pass through the training data. The training data has 200 items, therefore, one training epoch consists of processing 20 batches of 10 training items.
During training, the demo computes and displays a measure of the current error (also called loss) every 50 epochs. Because error slowly decreases, it appears that training is succeeding. Behind the scenes, the demo program saves checkpoint information after every 50 epochs so that if the training machine crashes, training can be resumed without having to start over from the beginning.
After training the network, the demo program computes the prediction accuracy of the model based on whether or not the predicted house price is within 10 percent of the true house price. The accuracy on the training data is 93.00 percent (186 out of 200 correct) and the accuracy on the test data is 92.50 percent (37 out of 40 correct). Because the two accuracy values are similar, it is likely that model overfitting has not occurred.
Next, the demo uses the trained model to make a prediction on a new, previously unseen house. The raw input is (air conditioning = "no", square feet area = 2300, style = "colonial", school = "kennedy"). The raw input is normalized and encoded as (air conditioning = -1, area = 0.2300, style = 0,0,1, school = 0,1,0). The computed output price is 0.49104896 which is equivalent to $491,048.96 because the raw house prices were all normalized by dividing by 1,000,000.
The demo program concludes by saving the trained model using the state dictionary approach. This is the most common of three standard techniques.
This article assumes you have an intermediate or better familiarity with a C-family programming language, preferably Python, but doesn't assume you know very much about PyTorch. The complete source code for the demo program, and the two data files used, are available in the download that accompanies this article. All normal error checking code has been omitted to keep the main ideas as clear as possible.
To run the demo program, you must have Python and PyTorch installed on your machine. The demo programs were developed on Windows 10 using the Anaconda 2020.02 64-bit distribution (which contains Python 3.7.6) and PyTorch version 1.7.0 for CPU installed via pip. You can find detailed step-by-step installation instructions for this configuration in my blog post.
The House Data
The raw House data is synthetic and was generated programmatically. There are a total of 240 data items, divided into a 200-item training dataset and a 40-item test dataset. The raw data looks like:
no 1275 bungalow $318,000.00 lincoln
yes 1100 art_deco $335,000.00 johnson
no 1375 colonial $286,000.00 kennedy
yes 1975 bungalow $512,000.00 lincoln
. . .
no 2725 art_deco $626,000.00 kennedy
Each line of tab-delimited data represents one house. The value to predict, house price, is in 0-based column [3]. The predictors variables in columns [0], [1], [2] and [4] are air conditioning yes-no, area in square feet, architectural style and local school. For simplicity, there are just three house styles and three schools.
House area values were normalized by dividing by 10,000 and house prices were normalized by dividing by 1,000,000. Air conditioning was binary encoded as no = -1, yes = +1. Style was one-hot encoded as "art_deco" = (1,0,0), "bungalow" = (0,1,0), "colonial" = (0,0,1). School was one-hot encoded as "johnson" = (1,0,0), "kennedy" = (0,1,0), "lincoln" = (0,0,1). The resulting normalized and encoded data looks like:
-1 0.1275 0 1 0 0.3180 0 0 1
1 0.1100 1 0 0 0.3350 1 0 0
-1 0.1375 0 0 1 0.2860 0 1 0
1 0.1975 0 1 0 0.5120 0 0 1
. . .
-1 0.2725 1 0 0 0.6260 0 1 0
After the structure of the training and test files was established, I designed and coded a PyTorch Dataset class to read the house data into memory and serve the data up in batches using a PyTorch DataLoader object. A Dataset class definition for the normalized and encoded House data is shown in Listing 1.
Listing 1: A Dataset Class for the Student Data
class HouseDataset(T.utils.data.Dataset):
# AC sq ft style price school
# -1 0.2500 0 1 0 0.5650 0 1 0
# 1 0.1275 1 0 0 0.3710 0 0 1
# air condition: -1 = no, +1 = yes
# style: art_deco, bungalow, colonial
# school: johnson, kennedy, lincoln
def __init__(self, src_file, m_rows=None):
all_xy = np.loadtxt(src_file, max_rows=m_rows,
usecols=[0,1,2,3,4,5,6,7,8], delimiter="\t",
comments="#", skiprows=0, dtype=np.float32)
tmp_x = all_xy[:,[0,1,2,3,4,6,7,8]]
tmp_y = all_xy[:,5].reshape(-1,1) # 2-D
self.x_data = T.tensor(tmp_x, \
dtype=T.float32).to(device)
self.y_data = T.tensor(tmp_y, \
dtype=T.float32).to(device)
def __len__(self):
return len(self.x_data)
def __getitem__(self, idx):
preds = self.x_data[idx,:] # or just [idx]
price = self.y_data[idx,:]
return (preds, price) # tuple of matrices
Preparing data and defining a PyTorch Dataset is not trivial. You can find the article that explains how to create Dataset objects and use them with DataLoader objects here.
The Neural Network Architecture
In the previous article in this series, I described how to design and implement a neural network for regression for the House data. One possible definition is presented in Listing 2. The code defines an 8-(10-10)-3 neural network with relu() activation on the hidden nodes.
Listing 2: A Neural Network for the Student Data
class Net(T.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hid1 = T.nn.Linear(8, 10) # 8-(10-10)-1
self.hid2 = T.nn.Linear(10, 10)
self.oupt = T.nn.Linear(10, 1)
T.nn.init.xavier_uniform_(self.hid1.weight)
T.nn.init.zeros_(self.hid1.bias)
T.nn.init.xavier_uniform_(self.hid2.weight)
T.nn.init.zeros_(self.hid2.bias)
T.nn.init.xavier_uniform_(self.oupt.weight)
T.nn.init.zeros_(self.oupt.bias)
def forward(self, x):
z = T.relu(self.hid1(x))
z = T.relu(self.hid2(z))
z = self.oupt(z) # no activation
return z
If you are new to PyTorch, the number of design decisions for a neural network can seem intimidating. But with every program you write, you learn which design decisions are important and which don't affect the final prediction model very much, and the pieces of the design puzzle eventually fall into place.
The Overall Program Structure
The overall structure of the PyTorch neural regression program, with a few minor edits to save space, is shown in Listing 3. I prefer to indent my Python programs using two spaces rather than the more common four spaces.
Listing 3: The Structure of the Demo Program
# house_price.py
# PyTorch 1.7.0-CPU Anaconda3-2020.02
# Python 3.7.6 Windows 10
import numpy as np
import time
import torch as T
device = T.device("cpu")
class HouseDataset(T.utils.data.Dataset):
# AC sq ft style price school
# -1 0.2500 0 1 0 0.5650 0 1 0
# 1 0.1275 1 0 0 0.3710 0 0 1
# air condition: -1 = no, +1 = yes
# style: art_deco, bungalow, colonial
# school: johnson, kennedy, lincoln
def __init__(self, src_file, m_rows=None): . . .
def __len__(self): . . .
def __getitem__(self, idx): . . .
# ----------------------------------------------------
def accuracy(model, ds): . . .
# ----------------------------------------------------
class Net(T.nn.Module):
def __init__(self): . . .
def forward(self, x): . . .
# ----------------------------------------------------
def main():
# 0. get started
print("Begin predict House price ")
T.manual_seed(4)
np.random.seed(4)
# 1. create Dataset and DataLoader objects
# 2. create neural network
# 3. train network
# 4. evaluate model
# 5. make a prediction
# 6. save model
print("End House price demo ")
if __name__== "__main__":
main()
It's important to document the versions of Python and PyTorch being used because both systems are under continuous development. Dealing with versioning incompatibilities is a significant headache when working with PyTorch and is something you should not underestimate.
I like to use "T" as the top-level alias for the torch package. Most of my colleagues don't use a top-level alias and spell out "torch" many of times per program. Also, I use the full form of sub-packages rather than supplying aliases such as "import torch.nn.functional as functional." In my opinion, using the full form is easier to understand and less error-prone than using many aliases.
The demo program defines a program-scope CPU device object. I usually develop my PyTorch programs on a desktop CPU machine. After I get that version working, converting to a CUDA GPU system only requires changing the global device object to T.device("cuda") plus a minor amount of debugging.
The demo program defines just one helper method, accuracy(). All of the rest of the program control logic is contained in a single main() function. It is possible to define other helper functions such as train_net(), evaluate_model() and save_model(), but in my opinion this modularization approach unexpectedly makes the program more difficult to understand rather than easier to understand.
Training the Neural Network
The details of training a neural network with PyTorch are complicated but the code is relatively simple. In very high-level pseudo-code, the process to train a neural network looks like:
loop max_epochs times
loop thru all batches of train data
read a batch of data (inputs, targets)
compute outputs using the inputs
compute error between outputs and targets
use error to update weights and biases
end-loop (all batches)
end-loop (all epochs)
The difficult part of training is the "use error to update weights and biases" step. PyTorch does most, but not all, of the hard work for you. It's not easy to understand neural network training without seeing a working program. The test program shown in Listing 4 demonstrates how to train a network for multi-class classification. The screenshot in Figure 2 shows the output from the test program.
Listing 4: Testing Neural Network Training Code
# test_training.py
import numpy as np
import time
import torch as T
device = T.device("cpu")
class HouseDataset(T.utils.data.Dataset):
def __init__(self, src_file, m_rows=None):
all_xy = np.loadtxt(src_file, max_rows=m_rows,
usecols=[0,1,2,3,4,5,6,7,8], delimiter="\t",
comments="#", skiprows=0, dtype=np.float32)
tmp_x = all_xy[:,[0,1,2,3,4,6,7,8]]
tmp_y = all_xy[:,5].reshape(-1,1) # 2-D
self.x_data = T.tensor(tmp_x, \
dtype=T.float32).to(device)
self.y_data = T.tensor(tmp_y, \
dtype=T.float32).to(device)
def __len__(self):
return len(self.x_data)
def __getitem__(self, idx):
preds = self.x_data[idx,:] # or just [idx]
price = self.y_data[idx,:]
return (preds, price) # tuple of matrices
class Net(T.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hid1 = T.nn.Linear(8, 10) # 8-(10-10)-1
self.hid2 = T.nn.Linear(10, 10)
self.oupt = T.nn.Linear(10, 1)
T.nn.init.xavier_uniform_(self.hid1.weight)
T.nn.init.zeros_(self.hid1.bias)
T.nn.init.xavier_uniform_(self.hid2.weight)
T.nn.init.zeros_(self.hid2.bias)
T.nn.init.xavier_uniform_(self.oupt.weight)
T.nn.init.zeros_(self.oupt.bias)
def forward(self, x):
z = T.relu(self.hid1(x))
z = T.relu(self.hid2(z))
z = self.oupt(z) # no activation
return z
print("\nBegin test of training code\n")
T.manual_seed(1)
np.random.seed(1)
train_file = ".\\Data\\houses_train.txt"
train_ds = HouseDataset(train_file, m_rows=200)
bat_size = 10
train_ldr = T.utils.data.DataLoader(train_ds,
batch_size=bat_size, shuffle=True)
net = Net().to(device)
net.train() # set mode
lrn_rate = 0.005
loss_func = T.nn.MSELoss()
optimizer = T.optim.Adam(net.parameters(),
lr=lrn_rate)
for epoch in range(0, 500):
# T.manual_seed(1 + epoch) # recovery reproduce
epoch_loss = 0.0 # sum avg loss per item
for (batch_idx, batch) in enumerate(train_ldr):
X = batch[0] # predictors shape [10,8]
Y = batch[1] # targets shape [10,1]
optimizer.zero_grad()
oupt = net(X) # shape [10,1]
loss_val = loss_func(oupt, Y) # avg loss in batch
epoch_loss += loss_val.item() # a sum of averages
loss_val.backward()
optimizer.step()
if epoch % 100 == 0:
print(" epoch = %4d loss = %0.4f" % \
(epoch, epoch_loss))
# TODO: save checkpoint
print("\nDone ")
The training demo program begins execution with:
T.manual_seed(1)
np.random.seed(1)
train_file = ".\\Data\\houses_train.txt"
train_ds = HouseDataset(train_file, m_rows=200)
The global PyTorch and NumPy random number generator seeds are set so that results will be reproducible. Unfortunately, due to multiple threads of execution, in some cases your results will not be reproducible even if you set the seed values.
The demo assumes that the training data is located in a subdirectory named Data. The HouseDataset object reads all 200 training data items into memory. If your training data size is very large you can read just part of the data into memory using the m_rows (maximum rows) parameter.
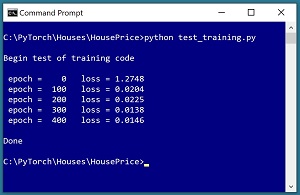 [Click on image for larger view.] Figure 2: Testing the Training Code
[Click on image for larger view.] Figure 2: Testing the Training Code
The demo program prepares training with these statements:
bat_size = 10
train_ldr = T.utils.data.DataLoader(train_ds,
batch_size=bat_size, shuffle=True)
net = Net().to(device)
net.train() # set mode
The training data loader is configured to read batches of 10 items at a time. In theory, the batch size doesn't matter too much, but in practice the batch size greatly affects how quickly training works. When you have a choice, it makes sense to use a batch size that divides the dataset size evenly so that all batches have the same size. Because the demo test House data has 200 rows, there will be 20 batches of 10 items each and no leftover items. It is very important to set shuffle=True when training because the default value is False which will often result in failed training.
After the neural network is created, it is set into training mode using the statement net.train(). If your neural network has a dropout layer or a batch normalization layer, you must set the network to train() mode during training and to eval() mode when using the network at any other time, such as making a prediction or computing model classification accuracy. The default state is train() mode so setting the mode isn't necessary for the demo network for two reasons: it's already in train() mode, and it doesn't use dropout or batch normalization. However, in my opinion it's good practice to always explicitly set the network mode.
The train() mode method works by reference so you can write just net.train() instead of net = net.train(). Note that the statement net.train() looks like it's an instruction to train a net object, but that is not what's happening.
The demo continues training preparation with these three statements:
lrn_rate = 0.005
loss_func = T.nn.MSELoss()
optimizer = T.optim.Adam(net.parameters(),
lr=lrn_rate)
For regression problems, the most common loss (error) function is MSELoss (mean squared error loss). In some rare cases you can use BCELoss (binary cross entropy) but only if all target values in the training data have been normalized to a [0, 1] range, and all computed output values are scaled to a [0, 1] range using logistic sigmoid activation.
The demo program uses the Adam ("adaptive momentum") training optimizer. Adam often works better than basic SGD ("stochastic gradient descent") for regression problems.
PyTorch 1.7 supports 11 different training optimization techniques. Understanding all the details of PyTorch optimizers is difficult. Each technique's method has several parameters which are quite complex and which often have a dramatic effect on training performance. See the list in Figure 3.
 [Click on image for larger view.] Figure 3: PyTorch Optimizers
[Click on image for larger view.] Figure 3: PyTorch Optimizers
Fortunately, almost all of the PyTorch optimizer parameters have reasonable default values. As a general rule of thumb, for regression problems I start by trying Adam with default parameter values. Then if I don't get good results, I'll adjust the learning rate parameter. If training still doesn't work, I'll try SGD.
A learning rate controls how much a network weight or bias changes on each update during training. For Adam it's best to use a small initial learning rate because the algorithm can dynamically change the learning rate during training.
The key takeaway is that if you're new to PyTorch you could easily spend weeks exploring the nuances of different training optimizers and never get any programs written. Optimizers are important but it's better to learn about different optimizers by experimenting with them slowly over time, with different problems, than it is to try and master all their details before writing any code.
After training has been prepared, the demo program starts the training:
for epoch in range(0, 500):
# T.manual_seed(1 + epoch) # recovery reproduce
epoch_loss = 0.0 # sum avg loss per item
for (batch_idx, batch) in enumerate(train_ldr):
X = batch[0] # predictors shape [10,8]
Y = batch[1] # targets shape [10,1]
optimizer.zero_grad()
oupt = net(X) # shape [10,1]
. . .
Setting the manual seed inside the main training loop is necessary if you periodically save the model's weights and biases as checkpoints, so that if the training machine crashes during training, you can recover with the exact same state. Because the demo program doesn't save checkpoints, it's not necessary to set the seed, which is why that statement is commented out.
For each batch of 10 items, the sets of 8 predictor values are extracted as X and the 10 target house price values are extracted as Y. The inputs are fed to the network and the results are captured as oupt. The zero_grad() method resets the gradients of all weights and biases so that new gradients can be computed and used to update the weights and biases.
The demo continues with:
loss_val = loss_func(oupt, Y) # avg loss in batch
epoch_loss += loss_val.item() # a sum of averages
loss_val.backward() # compute gradients
optimizer.step() # update weights
It's important to monitor the error/loss during training so that you can tell if training is working or not. There are three main ways to monitor loss. An epoch_loss value is computed for each batch of input values. This batch loss value is the average of the loss values for each item in the batch. For example, if a batch has four items and the MSE loss values for each of the four items are (2.00, 7.00, 3.00, 6.00) then the computed batch loss is 18.00 / 4 = 4.50. The simplest approach is to just display the loss for either the first batch or the last batch for each training epoch. It's usually not feasible to print the loss value for every batch because there are just too many batches processed in almost all realistic scenarios.
A second approach for monitoring loss during training is to accumulate each batch loss value, and then after all the batches in one epoch have been processed in one epoch, you can display the sum of the batch losses. For example, if one epoch consists of 3 batches of data and the batch average MSE loss values are (2.50, 5.10, 1.30) then the sum of the batch losses is 2.50 + 5.10 + 1.30 = 8.90. This approach for monitoring loss is the one used by the demo program.
A third approach for monitoring loss is to compute an average loss per item for all training items. This is a bit tricky. First you would "un-average" the average loss value returned by the loss_func() method, by multiplying by the number of items in the batch, and then you'd accumulate the individual loss values. After all batches have been processed, you can compute an average loss per item over the entire dataset by dividing by the total number of training items. The code could look like this:
for epoch in range(0, 500):
sum_epoch_loss = 0.0
for (batch_idx, batch) in enumerate(train_ldr):
. . .
loss_val = loss_func(oupt, Y) # avg loss in batch
sum_vals = loss_val.item() * len(X) # "un-average"
sum_epoch_loss += sum_vals # accumulate
. . .
if epoch % 50 == 0:
avg_loss = sum_epoch_loss / len(train_ds) # average
print(avg_loss)
None of the three approaches for monitoring loss during training give values that are easy to interpret. The important thing is to watch the values to see if the loss values are decreasing. It is possible for training loss to values to bounce around a bit, where a loss value might increase briefly, especially if your batch size is small. Because there are many ways to monitor and display cross entropy loss for neural regression, loss values usually can't be compared for different systems unless you know the systems are computing and displaying loss in the exact same way.
The item() method is used when you have a tensor that has a single numeric value. The item() method extracts the single value from the associated tensor and returns it as a regular scalar value. Somewhat unfortunately (in my opinion), PyTorch 1.7 allows you to skip the call to item() so you can write the shorter epoch_loss += loss_val instead. Because epoch_loss is a non-tensor scalar, the interpreter will figure out that you must want to extract the value in the loss_val tensor. You can think of this mechanism as similar to implicit type conversion. However, the shortcut form without calling the item() method is slightly misleading in my opinion and so I use item() in most situations, even when it's not technically necessary.
The loss_val is a tensor that is the last value in the behind-the-scenes computational graph that represents the neural network being trained. The loss_val.backward() method uses the back-propagation algorithm to compute all the gradients associated with the weights and biases that a part of the network containing loss_val. Put another way, loss_val.backward() computes the gradients of the output node weights and bias, and then the hid2 layer gradients, and then the hid1 layer gradients.
The optimizer.step() statement uses the newly computed gradients to update all the weights and biases in the neural network so that computed output values will get closer to the target values. When you instantiate an optimizer object for a neural network, you must pass in the network parameters object and so the optimizer object effectively has full access to the network and can modify it.
The demo program concludes training with these statements:
. . .
optimizer.step()
if epoch % 100 == 0:
print("epoch = %4d loss = %0.4f" % \
(epoch, epoch_loss))
# TODO: save checkpoint
print("Done ")
After all batches have been processed, a training epoch has been completed and program execution exits the innermost for-loop. Although it's possible to display the accumulated loss value for every epoch, in most cases that's too much information and so the demo just displays the accumulated average loss once every 100 epochs. In some problem scenarios you might want to store all accumulated epoch loss values in memory, and then save them all to a text file after training completes. This allows you to analyze training without slowing it down.
Because training a neural network can take hours, days, or even longer, in all non-demo scenarios you'd want to periodically save training checkpoints. This topic will be explained in the next article in this series.
Wrapping Up
Training a PyTorch neural network for a regression problem is simple and complicated at the same time. Training in PyTorch works at a low level. This requires a lot of effort but gives you maximum flexibility. The behind-the-scenes details and options such as optimizer parameters are very complex. But the good news is that the demo training code presented in this article can be used as a template for most of the neural regression problems you're likely to encounter.
Monitoring mean squared error/loss during training allows you to determine if training is working, but loss isn't a good way to evaluate a trained model. Ultimately prediction accuracy is the metric that's usually most important. Computing model accuracy, and saving a trained model to file, are topics in the next article in this series.