The Data Science Lab
Quantum-Inspired Annealing Using C# or Python
Dr. James McCaffrey of Microsoft Research explains a new idea that slightly modifies standard simulated annealing by borrowing ideas from quantum mechanics.
The goal of a combinatorial optimization problem is to find the best ordering of a set of discrete items. A classic combinatorial optimization challenge is the Traveling Salesman Problem (TSP). For TSP, you want to find the order in which to visit a set of cities so that the total distance traveled is minimized.
One of the oldest and simplest techniques for solving combinatorial optimization problems is called simulated annealing. A relatively new idea is to slightly modify standard simulated annealing by borrowing one or more ideas from quantum mechanics. This is sometimes called quantum-inspired annealing. Note that quantum-inspired algorithms do not use quantum computing hardware. Quantum-inspired algorithms are just modifications of existing classical algorithms, and they run on standard hardware.
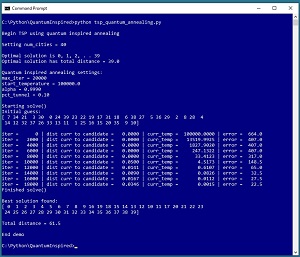
A good way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. The demo sets up a synthetic problem where there are 40 cities, labeled 0 through 39. The distance between cities is designed so that the best route starts at city 0 and then visits each city in order. The total distance of the optimal route is 39.0.
The demo sets up quantum-inspired annealing parameters of max_iter = 20_000, start_temperature = 100_000.0, alpha = 0.9990, and pct_tunnel = 0.10. Quantum-inspired annealing is an iterative process and max_iter is the maximum number of times the processing loop will execute. The start_temperature and alpha parameters control how the classical part of the annealing algorithm explores possible solution routes. The pct_tunnel parameter controls how often the quantum-inspired part of the algorithm is used.
The demo sets up a random initial guess of the best route as [ 7, 34, 21 . . 9, 10 ]. After iterating 20,000 times, the demo reports the best route found as [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 16, 19, 18, 15, 14, 13, 12, 10, 11, 17, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39 ]. The total distance required to visit the cities in this order is 61.5 and so the solution is close to, but not quite as good as, the optimal solution. The first 10 cities and the last 20 cities are visited in correct order but the middle 10 cities are not visited correctly.
 [Click on image for larger view.] Figure 1: Quantum-Inspired Annealing to Solve the Traveling Salesman Problem
[Click on image for larger view.] Figure 1: Quantum-Inspired Annealing to Solve the Traveling Salesman Problem
This article assumes you have an intermediate or better familiarity with a C-family programming language, preferably C# or Python, but does not assume you know anything about simulated annealing. The complete source code for the demo program is presented in this article, and the code is also available in the accompanying file download.
Understanding Classical Simulated Annealing
Quantum-inspired annealing is a slight adaptation of classical simulated annealing. Suppose you have a combinatorial optimization problem with just five elements, and where the best ordering/permutation is [B, A, D, C, E]. A primitive approach would be to start with a random permutation such as [C, A, E, B, D] and then repeatedly swap randomly selected pairs of elements until you find the best ordering. For example, if you swap the elements at [0] and [1], the new permutation is [A, C, E, B, D]. You'd repeat generating new permutations until you found a good result.
This brute force approach works if there are just a few elements in the problem permutation, but fails for even a moderate number of elements. For the demo problem with n = 40 cities, there are 40! possible permutations = 40 * 39 * 38 * . . * 1 = 815,915,283,247,897,734,345,611,269,596,115,894,272,000,000,000. Even if you could examine one billion candidate solutions per second, to check all permutations would take you roughly 9,000,000,000,000,000,000,000,000,000,000,000 years, which is much longer than the estimated age of the universe (about 14,000,000,000 years).
To understand quantum-inspired annealing you must first understand classical simulated annealing. Expressed as pseudo-code, classical simulated annealing is:
make a random initial guess permutation
set a large initial temperature
loop many times
swap two randomly selected elements of the curr guess
compute error of proposed candidate solution
if proposed solution is better than curr solution then
accept the proposed solution
else if proposed solution is worse then
sometimes accept solution anyway, based on curr temp
end-if
decrease temperature value slightly
end-loop
return best solution found
By swapping two randomly selected elements of the current solution, an adjacent proposed solution is created. The adjacent proposed solution will be similar to the current guess so the search process isn't completely random. A good current solution will likely lead to a good new proposed solution.
By sometimes accepting a proposed solution that's worse than the current guess, you can avoid getting trapped into a good but not optimal solution. The probability of accepting a worse solution is given by:
accept_p = exp((err - adj_err) / curr_temperature)
where exp() the mathematical exp() function, err is the error associated with the current guess, adj_err is the error associated with the proposed adjacent solution, and curr_temperature is a value such as 1000.0.
In simulated annealing, the temperature value starts out large, such as 1000000.0 and then is reduced slowly on each iteration. Early in the algorithm, when temperature is large, accept_p will be large (close to 1) and the algorithm will often move to a worse solution. This allows many permutations to be examined. Late in the algorithm, when temperature is small, accept_p will be small (close to 0) and the algorithm will rarely move to a worse solution.
The temperature reduction is controlled by the alpha value. Suppose the current temperature = 1000.0 and alpha = 0.90. After the next processing iteration, temperature becomes 1000.0 * 0.90 = 900.0. After the next iteration temperature becomes 900.0 * 0.90 = 810.0. After a third iteration temperature becomes 810.0 * 0.90 = 729.0. And so on. Smaller values of alpha decrease temperature more quickly.
Adding Quantum Inspired Tunneling
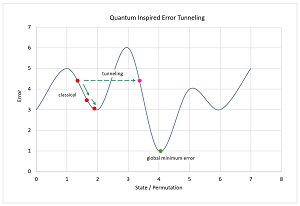
Quantum-inspired annealing adds a slight twist to classical simulated annealing. In quantum mechanics there is an idea called quantum tunneling. Briefly, and very loosely, a quantum particle will usually transition from its current energy state to an adjacent lower energy state. When a particle encounters a potential barrier it will usually be blocked, but will sometimes tunnel through the barrier to a non-adjacent state.
 [Click on image for larger view.] Figure 2: Quantum-Inspired Tunneling
[Click on image for larger view.] Figure 2: Quantum-Inspired Tunneling
This quantum tunneling can be used to improve classical simulated annealing. The key ideas are shown in the graph in Figure 2. In classical simulated annealing for TSP, the states are permutations of cities. If you transition only from the current state to an adjacent state (when the order of only one pair of cities is changed), you can get stuck at a local minimum error. If you allow tunneling, you can take a large jump to escape and get back on track to find the state with the global minimum error.
So, quantum-inspired tunneling just means sometimes allowing a candidate solution to be farther away from the current solution. This can be achieved by swapping more than just two cities. For example, if you swap 10 pairs of randomly selected cities, the result permutation will be father away from the source permutation than if you swap just one pair of randomly selected cities.
Early in the algorithm, when creating a candidate solution, you can swap many pairs of cities, generating a candidate that is far from the current permutation. Later in the algorithm you swap fewer pairs of cities. Expressed in pseudo-code:
set pct_tunnel (like 0.10)
loop many times
p = random in [0.0, 1.0)
if p < pct_tunnel then (do tunneling)
set num_swaps = large, based on pct iterations left
else
set num_swaps = 1 (no tunneling)
end-if
create candidate solution using num_swaps
apply classical annealing
end-loop
return best solution found
The Python version of the function that creates a candidate permutation-solution is:
def adjacent(route, n_swaps, rnd):
n = len(route)
result = np.copy(route)
for ns in range(n_swaps):
i = rnd.randint(n)
j = rnd.randint(n)
tmp = result[i]
result[i] = result[j]
result[j] = tmp
return result
The route parameter is the current solution. The n_swaps parameter specifies how many pair of cities to swap when creating the candidate solution. The rnd parameter is a local random number generator object.
An equivalent C# version of the function is:
static int[] Adjacent(int[] route, int numSwaps, Random rnd)
{
int n = route.Length;
int[] result = (int[])route.Clone();
for (int ns = 0; ns < numSwaps; ++ns) {
int i = rnd.Next(0, n);
int j = rnd.Next(0, n);
int tmp = result[i];
result[i] = result[j];
result[j] = tmp;
}
return result;
}
The key parameter is the number of pairs of cities to swap. The demo program computes this as the percent of iterations remaining times the total number of cities. For example, for n = 40 cities, if max_iterations = 1000 and the current iteration is 300, then there are 700 / 1000 = 0.70 of the iterations remaining, and the number of swaps would be 0.70 * 40 = 28.
The Demo Program
The complete quantum-inspired annealing demo program using Python, with a few minor edits to save space, is presented in Listing 1. I indent using two spaces rather than the standard four spaces. The backslash character is used for line continuation to break down long statements. You can find an equivalent C# version of the demo program on my blog.
Listing 1: The Quantum Annealing for TSP Python Language Program
# tsp_quantum_annealing.py
# traveling salesman problem
# quantum inspired simulated annealing
# Python 3.7.6 (Anaconda3 2020.02)
import numpy as np
def total_dist(route):
d = 0.0 # total distance between cities
n = len(route)
for i in range(n-1):
if route[i] < route[i+1]:
d += (route[i+1] - route[i]) * 1.0
else:
d += (route[i] - route[i+1]) * 1.5
return d
def error(route):
n = len(route)
d = total_dist(route)
min_dist = n-1
return d - min_dist
def adjacent(route, n_swaps, rnd):
# tunnel if n_swaps > 1
n = len(route)
result = np.copy(route)
for ns in range(n_swaps):
i = rnd.randint(n); j = rnd.randint(n)
tmp = result[i]
result[i] = result[j]; result[j] = tmp
return result
def my_kendall_tau_dist(p1, p2):
# p1, p2 are 0-based lists or np.arrays
n = len(p1)
index_of = [None] * n # lookup into p2
for i in range(n):
v = p2[i]; index_of[v] = i
d = 0 # raw distance = number pair misorderings
for i in range(n):
for j in range(i+1, n):
if index_of[p1[i]] > index_of[p1[j]]:
d += 1
normer = n * (n - 1) / 2.0
nd = d / normer # normalized distance
return (d, nd)
def solve_qa(n_cities, rnd, max_iter, start_temperature,
alpha, pct_tunnel):
curr_temperature = start_temperature
soln = np.arange(n_cities, dtype=np.int64) # [0,1,2, . . ]
rnd.shuffle(soln)
print("Initial guess: ")
print(soln); print("")
err = error(soln)
iter = 0
interval = (int)(max_iter / 10)
num_swaps = n_cities
best_soln = np.copy(soln)
best_err = err
while iter < max_iter and err > 0.0:
# while iter < max_iter:
# pct left determines n_swaps determines distance
pct_iters_left = (max_iter - iter) / (max_iter * 1.0)
if pct_iters_left < 0.00001:
pct_iters = 0.00001
p = rnd.random() # [0.0, 1.0]
if p < pct_tunnel: # tunnel
num_swaps = (int)(pct_iters_left * n_cities)
if num_swaps < 1:
num_swaps = 1
else: # no tunneling
num_swaps = 1
adj_route = adjacent(soln, num_swaps, rnd)
adj_err = error(adj_route)
if adj_err < best_err:
best_soln = np.copy(adj_route)
best_err = adj_err
if adj_err < err: # better route so accept
soln = adj_route; err = adj_err
else: # adjacent is worse
accept_p = np.exp((err - adj_err) / curr_temperature)
p = rnd.random()
if p < accept_p: # accept anyway
soln = adj_route
err = adj_err
# else don't accept worse route
if iter % interval == 0:
(dist, nd) = my_kendall_tau_dist(soln, adj_route)
print("iter = %6d | " % iter, end="")
print("dist curr to candidate = %8.4f | " \
% nd, end="")
print("curr_temp = %12.4f | " \
% curr_temperature, end="")
print("error = %6.1f " % best_err)
if curr_temperature < 0.00001:
curr_temperature = 0.00001
else:
curr_temperature *= alpha
iter += 1
return best_soln
def main():
print("\nBegin TSP using quantum inspired annealing ")
num_cities = 40
print("\nSetting num_cities = %d " % num_cities)
print("\nOptimal solution is 0, 1, 2, . . " + \
str(num_cities-1))
print("Optimal solution has total distance = %0.1f " \
% (num_cities-1))
rnd = np.random.RandomState(6)
max_iter = 20_000 # 120000 finds optimal solution
start_temperature = 100_000.0
alpha = 0.9990
pct_tunnel = 0.10
print("\nQuantum inspired annealing settings: ")
print("max_iter = %d " % max_iter)
print("start_temperature = %0.1f " \
% start_temperature)
print("alpha = %0.4f " % alpha)
print("pct_tunnel = %0.2f " % pct_tunnel)
print("\nStarting solve() ")
soln = solve_qa(num_cities, rnd, max_iter, \
start_temperature, alpha, pct_tunnel)
print("Finished solve() ")
print("\nBest solution found: ")
print(soln)
dist = total_dist(soln)
print("\nTotal distance = %0.1f " % dist)
print("\nEnd demo ")
if __name__ == "__main__":
main()
The demo program is structured so that all the control logic is in a main() function. The main() begins by setting up parameters for simulated annealing:
import numpy as np
def main():
print("Begin TSP using quantum inspired annealing ")
num_cities = 40
print("Setting num_cities = %d " % num_cities)
print("Optimal solution is 0, 1, 2, . . " + \
str(num_cities-1))
print("Optimal solution has total distance = %0.1f " \
% (num_cities-1))
rnd = np.random.RandomState(6)
max_iter = 20_000 # 120000 finds optimal solution
start_temperature = 100_000.0
alpha = 0.9990
pct_tunnel = 0.10
. . .
The program uses a local RandomState object rather than the numpy global object. This makes it easier to make program runs reproducible. The seed value of 6 was used only because it gave representative results. Finding good values for the max_iter, start_temperature, alpha, and pct_tunnel parameters is a matter of trial and error. The difficulty of parameter tuning is the biggest weakness of both classical simulated annealing and quantum-inspired annealing.
Next, the demo echoes the parameter values:
print("Quantum inspired annealing settings: ")
print("max_iter = %d " % max_iter)
print("start_temperature = %0.1f " \
% start_temperature)
print("alpha = %0.4f " % alpha)
print("pct_tunnel = %0.2f " % pct_tunnel)
The demo passes the quantum-inspired annealing parameters to a program-defined solve_qa() function:
print("Starting solve() ")
soln = solve_qa(num_cities, rnd, max_iter, \
start_temperature, alpha, pct_tunnel)
print("Finished solve() ")
The demo concludes by displaying the result:
print("Best solution found: ")
print(soln)
dist = total_dist(soln)
print("Total distance = %0.1f " % dist)
print("End demo ")
if __name__ == "__main__":
main()
Computing Distance Traveled
The demo defines a function that computes the total distance traveled for a specified route that visits all 40 cities:
def total_dist(route):
d = 0.0 # total distance between cities
n = len(route)
for i in range(n-1):
if route[i] < route[i+1]:
d += (route[i+1] - route[i]) * 1.0
else:
d += (route[i] - route[i+1]) * 1.5
return d
For any pair of from-to cities (A, B), if A is less than B then the distance between the two cities is 1.0 * (B - A). For example, the distance from city 4 to city 11 is 7.0. If B is less than A then the distance between cities is 1.5 * (A - B). For example, the distance from city 8 to city 1 is 7 * 1.5 = 10.5.
The distance for a route is the sum of the distances between the cities in the route. For example, the sub-route [4, 11, 5, 6] has distance 7.0 + 9.5 + 1.0 = 17.5. In a non-demo scenario you'd create a lookup table with actual distances.
If there are n cities, the demo design produces a problem where the optimal solution is [0, 1, 2, . . (n-1)] and the optimal minimum distance is 1.0 * (n-1). Therefore, it's possible to define an error function:
def error(route):
n = len(route)
d = total_dist(route)
min_dist = n-1
return d - min_dist
In a non-demo scenario, you won't know the optimal solution. In this situation you can define the error of a route as the distance of the route. A large distance is equivalent to large error because the goal is to minimize the total distance traveled.
The Distance Between Two Permutations
The main processing loop inside the solve_qa() function monitors progress every interval = 2,000 iterations:
if iter % interval == 0:
(dist, nd) = my_kendall_tau_dist(soln, adj_route)
print("iter = %6d | " % iter, end="")
print("dist curr to candidate = %8.4f | " \
% nd, end="")
print("curr_temp = %12.4f | " \
% curr_temperature, end="")
print("error = %6.1f " % best_err)
The solve_qa() function calls a program-defined my_kendall_tau_dist() function to compute the distance between the current permutation-guess and the proposed candidate permutation. Computing the distance/difference between two permutations is an interesting sub-problem. The Kendall Tau distance between two permutations is the number of pairs of elements that are ordered differently. Computing the distance between the current and candidate permutation isn't necessary for quantum-inspired annealing, but it's a good way to identify when no progress is being made.
Wrapping Up
Quantum tunneling is just one of many ideas from quantum mechanics that can be used to modify a standard optimization algorithm. For example, quantum particles have a charge property which affects their behavior, so you could create a packet of particles (where each particle corresponds to a candidate solution) and define different behaviors for positive and negative particles.
Classical and quantum-inspired annealing for combinatorial optimization require huge amounts of compute power for non-trivial problems. But as compute power increases -- for example, through massively parallel GPU processing in the Cloud -- quantum-inspired optimization algorithms are likely to become more useful. And when true quantum computing becomes readily available, it's possible that quantum-inspired deep neural network training could lead to breakthroughs that are difficult to imagine.