The Data Science Lab
Weighted k-NN Classification Using C#
Dr. James McCaffrey of Microsoft Research uses a complete program and step-by-step guidance to explain the machine learning technique, which can be used to predict a person's happiness score from their income and education, for example.
The goal of a weighted k-NN ("k-nearest neighbors") classification problem is to predict a discrete value called the class label. The idea is best explained by a concrete example. Suppose you have a set of 30 data items where each item consists of a person's annual income, their education (years) and their personality happiness score (0, 1 or 2). You want to predict a person's happiness score from their income and education. This is an example of multi-class classification because the variable to predict, happiness, has three or more possible values. If the variable to predict has just two possible values, the problem would be called binary classification. The k-NN technique can handle both multi-class and binary classification problems.
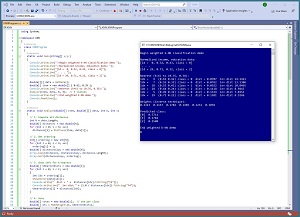[Click on image for larger view.] Figure 1: Weighted k-NN Classification Using C#
A good way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. The demo sets up 30 data items. Each has a data ID (from 0 to 29), annual income (normalized by dividing by $100,000), education (normalized by dividing by 20) and happiness score (0, 1, 2). The data items look like:
ID Income Education Happy
--------------------------
00 0.32 0.43 0
01 0.26 0.54 0
. . .
12 0.39 0.43 1
. . .
29 0.71 0.22 2
The graph in Figure 2 shows the data. The goal is to predict the happiness score of a person who has (income, education) of (0.62, 0.35). Notice that all the predictor values are numeric. This is a key characteristic of the k-NN classification technique presented in this article. If you have non-numeric predictor data, such as a person's age in years, you should use a different classification technique such as a neural network or decision tree.
The demo program specifies k = 6 and then computes the six closest data points to the (0.62, 0.35) item to classify. Of the six closest points, three are class 0, one is class 1, and two are class 2. A simple majority-rule voting scheme would conclude that (0.62, 0.35) is class 0. The demo uses a weighted voting scheme where closer data points receive more weight. The weighted votes are (0.5711, 0.1782, 0.2508). The largest value is at index [0] and so the prediction is happiness = 0.
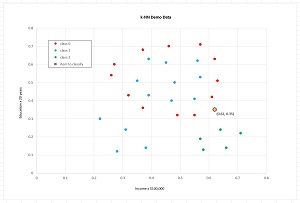[Click on image for larger view.] Figure 2: The k-NN Demo Data
This article assumes you have intermediate or better programming skill with C-family language such as Python or Java, but doesn't assume you know anything about weighted k-NN classification. The complete demo code and the associated data are presented in this article. The source code and the data are also available in the accompanying download. All normal error checking has been removed to keep the main ideas as clear as possible.
Understanding Weighted k-NN Classification
The first step in weighted k-NN classification is to compute the distances from the data item to predict to each of the data points. There are many ways to compute the distance between two points but Euclidean distance is simple and effective in most cases.
For example, the Euclidean distance between the target (0.62, 0.35) item and data point [09] at (0.61, 0.42) is:
dist = sqrt( (0.62 - 0.61)^2 + (0.35 - 0.42)^2 )
= sqrt( 0.0001 + 0.0049 )
= sqrt(0.0050)
= 0.0707
It's important for the numeric predictor values to be normalized so that variables with large magnitudes, such as income, don't overwhelm variables with smaller magnitudes.
The next step is to find the k-nearest data points to the target item. This is done by sorting all the distances and extracting the first k items and distances. For the demo data, the k = 6 closest items to (0.62, 0.35) are:
ID Data Class Dist Inv Dist
------------------------------------
09 (0.61 0.42) 0 0.0707 14.1421
07 (0.55 0.32) 0 0.0762 13.1306
18 (0.55 0.41) 1 0.0922 10.8465
28 (0.64 0.24) 2 0.1118 8.9443
05 (0.49 0.32) 0 0.1334 7.4953
29 (0.71 0.22) 2 0.1581 6.3246
To weight closer data items more heavily, the inverse of the distance is used. At this point you could just sum the inverse distances for each class like so:
class 0: 14.1421 + 13.1306 + 7.4953 = 34.7680
class 1: 10.8465
class 2: 8.9443 + 6.3246 = 15.2689
-------
60.8834
The prediction is the class with the highest weighted votes, class 0. The demo program normalizes the weighted votes by dividing each by their sum, which is 60.8834. This makes the weighted votes sum to 1.0 and a bit easier to interpret:
class 0: 34.7680 / 60.8834 = 0.5711
class 1: 10.8465 / 60.8834 = 0.1782
class 2: 15.2689 / 60.8834 = 0.2508
------
1.0000
The biggest weakness of k-NN classification is that there is no good way to select the value of k. For a given problem, different values of k often give different predictions. One technique to address this issue is to use several different values of k and then use the most common predicted class.
The Demo Program
The complete demo program, with a few minor edits to save space, is presented in Listing 1. To create the program, I launched Visual Studio and created a new C# .NET Core console application named KNN. I used Visual Studio 2019 (free Community Edition), but the demo has no significant dependencies so any version of Visual Studio will work fine. You can use the Visual Studio Code program too.
After the template code loaded, in the editor window I removed all unneeded namespace references, leaving just the reference to the top-level System namespace. In the Solution Explorer window, I right-clicked on file Program.cs, renamed it to the more descriptive KNNProgram.cs, and allowed Visual Studio to automatically rename class Program to KNNProgram.
Listing 1: Complete k-NN Demo Code
using System;
namespace KNN
{
class KNNProgram
{
static void Main(string[] args)
{
Console.WriteLine("Begin weighted k-NN classification demo ");
Console.WriteLine("Normalized income, education data: ");
Console.WriteLine("[id = 0, 0.32, 0.43, class = 0]");
Console.WriteLine(" . . . ");
Console.WriteLine("[id = 29, 0.71, 0.22, class = 2]");
double[][] data = GetData();
double[] item = new double[] { 0.62, 0.35 };
Console.WriteLine("\nNearest (k=6) to (0.35, 0.38):");
Analyze(item, data, 6, 3); // 3 classes
Console.WriteLine("\nEnd weighted k-NN demo ");
Console.ReadLine();
}
static void Analyze(double[] item, double[][] data, int k, int c)
{
// 1. Compute all distances
int N = data.Length;
double[] distances = new double[N];
for (int i = 0; i < N; ++i)
distances[i] = DistFunc(item, data[i]);
// 2. Get ordering
int[] ordering = new int[N];
for (int i = 0; i < N; ++i)
ordering[i] = i;
double[] distancesCopy = new double[N];
Array.Copy(distances, distancesCopy, distances.Length);
Array.Sort(distancesCopy, ordering);
// 3. Show info for k-nearest
double[] kNearestDists = new double[k];
for (int i = 0; i < k; ++i)
{
int idx = ordering[i];
ShowVector(data[idx]);
Console.Write(" dist = " +
distances[idx].ToString("F4"));
Console.WriteLine(" inv dist " +
(1.0 / distances[idx]).ToString("F4"));
kNearestDists[i] = distances[idx];
}
// 4. Vote
double[] votes = new double[c]; // one per class
double[] wts = MakeWeights(k, kNearestDists);
Console.WriteLine("\nWeights (inverse technique): ");
for (int i = 0; i < wts.Length; ++i)
Console.Write(wts[i].ToString("F4") + " ");
Console.WriteLine("\n\nPredicted class: ");
for (int i = 0; i < k; ++i)
{
int idx = ordering[i];
int predClass = (int)data[idx][3];
votes[predClass] += wts[i] * 1.0;
}
for (int i = 0; i < c; ++i)
Console.WriteLine("[" + i + "] " +
votes[i].ToString("F4"));
} // Analyze
static double[] MakeWeights(int k, double[] distances)
{
// Inverse technique
double[] result = new double[k]; // one per neighbor
double sum = 0.0;
for (int i = 0; i < k; ++i) {
result[i] = 1.0 / distances[i];
sum += result[i];
}
for (int i = 0; i < k; ++i)
result[i] /= sum;
return result;
}
static double DistFunc(double[] item, double[] dataPoint)
{
double sum = 0.0;
for (int i = 0; i < 2; ++i) {
double diff = item[i] - dataPoint[i + 1];
sum += diff * diff;
}
return Math.Sqrt(sum);
}
static double[][] GetData()
{
double[][] data = new double[30][];
data[0] = new double[] { 0, 0.32, 0.43, 0 };
data[1] = new double[] { 1, 0.26, 0.54, 0 };
data[2] = new double[] { 2, 0.27, 0.6, 0 };
data[3] = new double[] { 3, 0.37, 0.36, 0 };
data[4] = new double[] { 4, 0.37, 0.68, 0 };
data[5] = new double[] { 5, 0.49, 0.32, 0 };
data[6] = new double[] { 6, 0.46, 0.7, 0 };
data[7] = new double[] { 7, 0.55, 0.32, 0 };
data[8] = new double[] { 8, 0.57, 0.71, 0 };
data[9] = new double[] { 9, 0.61, 0.42, 0 };
data[10] = new double[] { 10, 0.63, 0.51, 0 };
data[11] = new double[] { 11, 0.62, 0.63, 0 };
data[12] = new double[] { 12, 0.39, 0.43, 1 };
data[13] = new double[] { 13, 0.35, 0.51, 1 };
data[14] = new double[] { 14, 0.39, 0.63, 1 };
data[15] = new double[] { 15, 0.47, 0.4, 1 };
data[16] = new double[] { 16, 0.48, 0.5, 1 };
data[17] = new double[] { 17, 0.45, 0.61, 1 };
data[18] = new double[] { 18, 0.55, 0.41, 1 };
data[19] = new double[] { 19, 0.57, 0.53, 1 };
data[20] = new double[] { 20, 0.56, 0.62, 1 };
data[21] = new double[] { 21, 0.28, 0.12, 1 };
data[22] = new double[] { 22, 0.31, 0.24, 1 };
data[23] = new double[] { 23, 0.22, 0.3, 1 };
data[24] = new double[] { 24, 0.38, 0.14, 1 };
data[25] = new double[] { 25, 0.58, 0.13, 2 };
data[26] = new double[] { 26, 0.57, 0.19, 2 };
data[27] = new double[] { 27, 0.66, 0.14, 2 };
data[28] = new double[] { 28, 0.64, 0.24, 2 };
data[29] = new double[] { 29, 0.71, 0.22, 2 };
return data;
}
static void ShowVector(double[] v)
{
Console.Write("idx = " + v[0].ToString().PadLeft(3) +
" (" + v[1].ToString("F2") + " " +
v[2].ToString("F2") + ") class = " + v[3]);
}
} // Program
} // ns
The demo program hard-codes the data inside a program-defined function GetData(). The data is returned as an array-of-arrays style double[ ][ ] matrix. In a non-demo scenario you might want to store data in a text file and write a helper function to read the data into an array-of-arrays matrix.
The first value in each data item is an arbitrary ID. I used consecutive integers from 0 to 29, but in many cases you'd have meaningful IDs such as a person's employee ID number. The k-NN algorithm doesn't need data IDs so the ID column could have been omitted. The second and third values are the normalized predictor values. The fourth value is the class ID. Class IDs for k-NN don't need to be zero-based integers, but using this scheme is convenient.
Computing Distances
The first step in the k-NN algorithm is to compute the distance from each labeled data item to the item-to-be classified. Based on my experience and a few research results, the choice of distance function to apply is not as critical as you might expect, and simple Euclidean distance usually works well.
The demo implementation of Euclidean distance is:
static double DistFunc(double[] item, double[] dataPoint)
{
double sum = 0.0;
for (int i = 0; i < 2; ++i) {
double diff = item[i] - dataPoint[i+1];
sum += diff * diff;
}
return Math.Sqrt(sum);
}
Notice that the for-loop indexing is hard-coded with 2 for the number of predictor values, and the difference between item[i] and dataPoint[i+1] is offset to account for the data ID value at position [0]. The point here is that there's usually a tradeoff between coding a machine learning algorithm for a specific problem and coding the algorithm with a view towards general purpose use. Because k-NN is so simple and easy to implement, I usually prefer the code-for-specific problem approach.
Sorting or Ordering the Distances
After all distances have been computed, the k-NN algorithm must find the k-nearest (smallest) distances. The approach used by the demo is to use a neat overload of the .NET Array.Sort method to sort just the distances and the associated data indices in parallel. The key code is:
int[] ordering = new int[N];
for (int i = 0; i < N; ++i)
ordering[i] = i;
double[] distancesCopy = new double[N];
Array.Copy(distances, distancesCopy, distances.Length);
Array.Sort(distancesCopy, ordering);
The array named ordering initially holds 0, 1, 2 . . 29. A copy of the 29 distances to the item-to-classify is created because you don't want to lose the distances in their original order. The statement Array,Sort(distancesCopy, ordering) sorts the values in the distancesCopy array from smallest to largest using the Quicksort algorithm, and simultaneously rearranges the index values in the ordering array. The result is that the first value in array ordering is the index in data of the item with the smallest distance, the second value in ordering holds the index to the second closest distance, and so on. A very nice feature of the C# language.
Wrapping Up
The two main advantages of weighted k-NN classification are 1.) it's simple to understand and implement, and 2.) the results are easily interpretable. The two main disadvantages of weighted k-NN classification are 1.) there is no principled way to choose the value of k, and 2.) the technique works well only with strictly numeric predictor values because it's usually not possible to define a good distance function for non-numeric data points.
For an example using Python, see the article "Weighted k-NN Classification Using Python."
About the Author
Dr. James McCaffrey works for Microsoft Research in Redmond, Wash. He has worked on several Microsoft products including Azure and Bing. James can be reached at [email protected].