The Data Science Lab
ANOVA Using C#
One use case for the analysis of variance statistics technique is asking if student performances are the same in three classrooms taught by the same teacher but with different textbooks, says Dr. James McCaffrey of Microsoft Research.
Analysis of variance (ANOVA) is a classical statistics technique that's used to infer if the means (averages) of three or more groups are all equal, based on samples from the groups. For example, suppose there are three different introductory computer science classes at a university. Each class is taught by the same teacher but uses a different textbook. You want to know if student performance is the same in all three classes or not.
You have an exam that evaluates computer science proficiency on a 1-to-15 scale, but because the exam is expensive and time-consuming to administer, you can give the exam to at most six randomly selected students in each class. You administer the exam and perform ANOVA on the three samples to infer if the means of all three classes are the same or not.
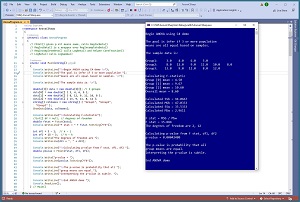 [Click on image for larger view.] Figure 1: ANOVA Using C# in Action
[Click on image for larger view.] Figure 1: ANOVA Using C# in Action
A good way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. The demo program sets up three samples: (3, 4, 6, 5), (8, 12, 9, 11, 10, 8) and (13, 9, 11, 8, 12). The means of the three samples are 4.50, 9.67 and 10.60. The sample means of the second and third groups look similar, but the mean of the first sample is quite a bit lower than the other two.
The overall mean of the 15 sample values is 8.60. The demo program computes intermediate SSb and SSw ("sum of squared") values and uses them to compute MSb and MSw ("mean squared") values. The computed F-statistic is MSb / MSw = 15.884.
Each set of data in an ANOVA problem has two df ("degrees of freedom") values. For the demo data, df1 = number groups minus one = 3 - 1 = 2, and df2 = total number of values minus number groups = 15 - 3 = 12.
The F-statistic and the two df values are used to compute a p-value = 0.0004. The p-value, very loosely, is the probability that all three source population means are the same based on the evidence computed from the three samples. Because the p-value is so small, you would conclude that it's unlikely the three source populations have the same mean.
The demo program does not check three ANOVA assumptions:
- The source data populations are all Normal (Gaussian, bell-shaped) distributed
- The variances of the source data populations are the same
- The sample observations are independent of each other
This article assumes you have intermediate or better programming skill with the C# language but doesn't assume you know anything about ANOVA. The demo code is a bit too long to present in its entirety in this article, but you can find the complete source code in the accompanying file download.
To create the demo program I used Visual Studio 2022 (the free Community edition) with .NET 5 (to avoid the strange new .NET 6 Console template). However, the demo has no significant dependencies so any relatively recent versions of VS and .NET can be used.
Computing the F-Statistic
Computing the F-statistic from samples of data is best explained by example. Suppose, as in the demo, there are three groups of samples:
Group 1: 3, 4, 6, 5
Group 2: 8, 12, 9, 11, 10, 8
Group 3: 13, 9, 11, 8, 12
The means of each sample group and the overall mean are:
Mean 1: (3 + 4 + 6 + 5) / 4 = 18 / 4 = 4.50
Mean 2: (8 + 12 + . . + 8) / 6 = 58 / 6 = 9.67
Mean 3: (13 + 9 + . . + 12) / 5 = 53 / 5 = 10.60
Overall: (3 + 4 + . . + 12) / 15 = 129 / 15 = 8.60
The SSb ("sum of squares between groups") is the weighted sum of squared differences between each group mean and the overall mean:
SSb = 4 * (4.50 - 8.60)^2 +
6 * (9.67 - 8.60)^2 +
5 * (10.60 - 8.60)^2
= 94.07
The MSb ("mean sum of squares between groups") = SSb / (k - 1) where k is the number of groups. For the demo data:
MSb = SSb / (3 - 1)
= 94.07 / (3 - 1)
= 47.03
The SSw ("sum of squares within groups") is the sum of squared differences between each sample data point and its associated group mean. For the demo data:
SSw = (3 - 4.50)^2 + (4 - 4.50)^2 + . . + (12 - 10.60)^2
= 35.53
The MSw ("mean sum of squares within groups") = SSw / (N - k) where N is the total number of sample data points and k is the number of groups:
MSw = 35.53 / (15 - 3)
= 35.53 / 12
= 2.96
The F-statistic is just MSb divided by MSw:
F-stat = MSb / MSw
= 47.03 / 2.96
= 15.88
The larger the computed F-statistic is, the more likely it is that all population means are not all the same. Note that "not all the same" is not equivalent to "all different" -- "not all the same" means at least two are different.
Computing the P-Value from the F-Statistic
The p-value is the area under the associated F-distribution, from the computed F-statistic value to positive infinity. The idea is best explained using a graph. See Figure 2.
There isn't just one F-distribution, there are many. There is a different F-distribution for each pair of df1 and df2 values. This is similar to the way that there is a different Normal (Gaussian, bell-shaped) distribution for each pair of (mean, standard deviation) values.
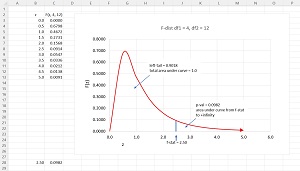 [Click on image for larger view.] Figure 2: Example of One F-Distribution
[Click on image for larger view.] Figure 2: Example of One F-Distribution
The graph in Figure 2 shows the F-distribution for df1 = 4 and df2 = 12. Unlike the Gaussian distributions that all have a bell-shape, the shapes of different F-distributions look quite different from each other.
The total area under any F-distribution is exactly 1. The p-value is the area of the right-tail: the area under the curve from the F-statistic to positive infinity. In the graph, each rectangle has an area of 0.10. If you look closely, you can see that the area in the right-tail is about one rectangle, and in fact the exact p-value is 0.0982.
Computing the area under an F-distribution is difficult. There are several different approaches. The demo program uses the "regularized incomplete beta" function to compute a p-value. The regularized incomplete beta function is often written as Ix(a, b) or I(x; a, b). You can think of I(x; a, b) as an abstract math function that accepts an x value between 0.0 and 1.0 and positive a and b values.
Although the math is deep, computing a p-value from an F-statistic, df1 and df2 is simple:
x = df2 / (df2 + df1 * f-stat)
a = df2 / 2
b = df1 / 2
p-value = I(x, a, b)
Easy. But implementing the I(x; a, b) function is widely regarded as one of the most difficult problems in scientific programming. Briefly, I(x; a, b) can be computed using the log-beta function, and the log-beta function can be computed using the log-gamma function.
A previous Visual Studio Magazine article titled "The LogBeta and LogGamma Functions Using C#" explains how to compute the I(x; a, b) function in detail.
The Demo Program
The demo program begins by setting up three groups of sample data:
static void Main(string[] args)
{
double[][] data = new double[3][]; // 3 groups
data[0] = new double[] { 3, 4, 6, 5 };
data[1] = new double[] { 8, 12, 9, 11, 10, 8 };
data[2] = new double[] { 13, 9, 11, 8, 12 };
string[] colNames = new string[] { "Group1", "Group2",
"Group3" };
ShowData(data, colNames);
. . .
The ShowData() function is just a program-defined helper to display the data in a nice format. Next, the demo data is used to find the computed F-statistic:
Console.WriteLine("Calculating F-statistic");
double fstat = Fstat(data);
Console.WriteLine("F stat = " + fstat.ToString("F3"));
The program-defined Fstat() function computes group means, the overall mean, MSb and MSw as explained in this article.
The p-value is computed from the degrees of freedom values and the computed f-statistic like so:
int df1 = 3 - 1; // k - 1
int df2 = 15 - 3; // N - k
Console.Write("The degrees of freedom are ");
Console.WriteLine(df1 + ", " + df2);
Console.WriteLine("Calculating p-value ");
double pValue = FDist(fstat, df1, df2);
Console.Write("p-value = ");
Console.WriteLine(pValue.ToString("F8"));
The demo program hard-codes the df1 and df2 values. An alternative approach is to compute df1 and df2 programmatically from the sample data.
The FDist() Function
The key to the demo is the FDist() function that computes the p-value. It is defined as:
static double FDist(double fstat, double df1, double df2)
{
double x = df2 / (df2 + df1 * fstat);
double a = df2 / 2;
double b = df1 / 2;
return RegIncBeta(x, a, b); // p-value
}
The FDist() function is deceptively simple-looking because all of the difficult work is done by the RegIncBeta() function. The RegIncBeta() function is a wrapper over a RegIncompleteBeta() function, which calls helper functions LogBeta() and ContFraction().
Wrapping Up
It is very important to remember that the results of an ANOVA analysis are probabilistic and should be interpreted conservatively. For real-world data, the computed p-value is only an indication of the likelihood that the source population means are all the same. For small p-values (where "small" depends on your particular problem scenario), an appropriate conclusion is something like, "the sample data suggest that it's unlikely that the population means are all the same." For large p-values, an appropriate conclusion is, "the sample data suggest that all k source populations likely have the same mean."
As the demo data illustrates, a small p-value does not suggest that all source population means are different. It's possible that two or more populations means could be the same.
One significant weakness of ANOVA is that it's often impossible to test the assumptions that the data sources are Gaussian distributed and have equal variances. This is another reason why ANOVA conclusions should be conservative.
ANOVA is intended for scenarios with three or more sample groups. A closely related classical statistics technique is called the Student's t-test. The t-test is used to compare the means of exactly two groups. It is possible to use ANOVA for just two groups, but the t-test is a more common approach.
About the Author
Dr. James McCaffrey works for Microsoft Research in Redmond, Wash. He has worked on several Microsoft products including Azure and Bing. James can be reached at [email protected].