Neural Network Lab
Classification Using Perceptrons
Learn how to create a perceptron that can categorize inputs consisting of two numeric values.
A perceptron is computer code that models the behavior of a single biological neuron. Perceptrons were one of the very earliest types of machine-learning techniques and are the predecessors to neural networks. Although perceptrons are quite limited, learning about perceptrons might interest you for several reasons. Understanding perceptrons gives you a foundation for understanding neural networks, knowledge of perceptrons is almost universal in the machine-learning community and, in my opinion, perceptrons are conceptually interesting in their own right.
Take a look at a demo C# console application in Figure 1 to get an idea of where this article is headed. The goal of the demo is to create a perceptron that can categorize input that consists of two numeric values (such as 1.0, 4.5) into one of two classes (-1 or +1). The first part of the screenshot shows that there are 16 training data items with known classifications. For example, the first training item input is (-5.0, -5.5) and its corresponding class is -1. You can imagine that the two inputs might be the results of two medical tests and that the classification represents the presence (+1) or absence (-1) of some disease.
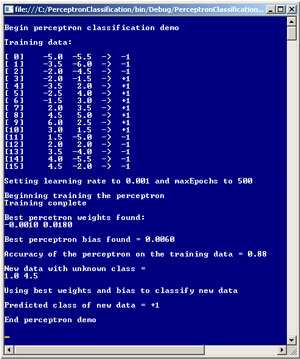 [Click on image for larger view.]
Figure 1. Perceptron classification demo.
[Click on image for larger view.]
Figure 1. Perceptron classification demo.
The next part of the screenshot indicates that the perceptron uses the training data to compute two weights with values (-0.0010, 0.0180) and a bias term with value 0.0060. The training process uses a learning rate that has been set to 0.001 and a maxEpochs value of 500. The two weights and the bias term essentially define the behavior of the perceptron. After training, the perceptron correctly classifies 88 percent of the training data (14 out of 16 items).
After the perceptron has been created, it's presented with a new data item, (1.0, 4.5), that belongs to an unknown class. The perceptron predicts that the new data item belongs to class +1.
The Excel graph in Figure 2 illustrates the perceptron demo. Training data items that belong to class -1 are colored blue and are mostly below the x-axis. Training items that belong to class +1 are colored red. The new data item with unknown class is labeled with a question mark. You can intuit that the new item is most likely red, or belongs to class +1, as predicted by the perceptron.
 [Click on image for larger view.]
Figure 2. Perceptron classification visualization.
[Click on image for larger view.]
Figure 2. Perceptron classification visualization.
In the sections that follow, I'll walk you through the C# code for the demo program. This article assumes you have basic familiarity with perceptrons, and at least intermediate-level programming skills. You may want to read my previous column, "Modeling Neuron Behavior in C#," for an introduction to perceptrons.
Overall Program Structure
To create the perceptron demo program, I launched Visual Studio 2012 and created a new C# console application named PerceptronClassification. The demo program has no significant Microsoft .NET Framework dependencies, so any version of Visual Studio should work. After the template code loaded, I renamed file Program.cs in the Solution Explorer window to the more descriptive PerceptronClassificationProgram.cs, and Visual Studio automatically renamed the class containing the Main method for me. At the top of the code I deleted all using statements except for the one that references the System namespace. The overall program structure and the Main method, with a few minor edits, are presented in Listing 1.
Listing 1. Perceptron classification program structure.
using System;
namespace PerceptronClassification
{
class PerceptronClassificationProgram
{
static void Main(string[] args)
{
try
{
Console.WriteLine("\nBegin perceptron classification demo");
double[][] trainData = new double[16][];
trainData[0] = new double[] { -5.0, -5.5 };
trainData[1] = new double[] { -3.5, -6.0 };
trainData[2] = new double[] { -2.0, -4.5 };
trainData[3] = new double[] { -2.0, -1.5 };
trainData[4] = new double[] { -3.5, 2.0 };
trainData[5] = new double[] { -2.5, 4.0 };
trainData[6] = new double[] { -1.5, 3.0 };
trainData[7] = new double[] { 2.0, 3.5 };
trainData[8] = new double[] { 4.5, 5.0 };
trainData[9] = new double[] { 6.0, 2.5 };
trainData[10] = new double[] { 3.0, 1.5 };
trainData[11] = new double[] { 1.5, -5.0 };
trainData[12] = new double[] { 2.0, 2.0 };
trainData[13] = new double[] { 3.5, -4.0 };
trainData[14] = new double[] { 4.0, -5.5 };
trainData[15] = new double[] { 4.5, -2.0 };
int[] Y = new int[16] { -1, -1, -1, 1, 1, 1, 1, 1,
1, 1, 1, -1, -1, -1, -1, -1 };
Console.WriteLine("\nTraining data: \n");
ShowTrainData(trainData, Y);
double[] weights = null;
double bias = 0.0;
double alpha = 0.001;
int maxEpochs = 500;
Console.Write("\nSetting learning rate to " + alpha.ToString("F3"));
Console.WriteLine(" and maxEpochs to " + maxEpochs);
Console.WriteLine("\nBeginning training the perceptron");
Train(trainData, alpha, maxEpochs, Y, out weights, out bias);
Console.WriteLine("Training complete");
Console.WriteLine("\nBest percetron weights found: ");
ShowVector(weights, 4);
Console.Write("\nBest perceptron bias found = ");
Console.WriteLine(bias.ToString("F4"));
double acc = Accuracy(trainData, weights, bias, Y);
Console.Write("\nAccuracy of perceptron on training data = ");
Console.WriteLine(acc.ToString("F2"));
double[] unknown = new double[] { 1.0, 4.5 };
Console.WriteLine("\nNew data with unknown class = ");
ShowVector(unknown, 1);
Console.WriteLine("\nUsing best weights and bias to classify data");
int c = ComputeOutput(unknown, weights, bias);
Console.Write("\nPredicted class of new data = ");
Console.WriteLine(c.ToString("+0;-0"));
Console.WriteLine("\nEnd perceptron demo\n");
Console.ReadLine();
}
catch (Exception ex)
{
Console.WriteLine(ex.Message);
Console.ReadLine();
}
} // Main
static int ComputeOutput(double[] data, double[] weights,
double bias) { . . }
static int Activation(double x) { . . }
static double Accuracy(double[][] trainData, double[] weights,
double bias, int[] Y) { . . }
static double TotalError(double[][] trainData, double[] weights,
double bias, int[] Y) { . . }
static double Error(double[] data, double[] weights,
double bias, int Y) { . . }
static void Train(double[][] trainData, double alpha, int maxEpochs,
int[] Y, out double[] weights, out double bias) { . . }
static void ShowVector(double[] vector, int decimals) { . . }
static void ShowTrainData(double[][] trainData, int[] Y) { . . }
} // class
} // ns
The demo program consists of a Main method and eight helper methods. The program begins by setting up the 16 training data items in a matrix named trainData. For simplicity, and so that I could visualize the demo as a graph, each item has two type double values. Perceptrons can handle data with any number of dimensions. The classes (-1 or +1) for each training item are stored in a separate array named Y. The training data has been designed so that no perceptron can classify the data with 100 percent accuracy.
Helper method ShowTrainData is used to display the training data as shown in Figure 1. Next, the program declares a weights array and a bias variable. The values for weights and bias will be computed and returned as out parameters by method Train. Variable alpha, usually called the learning rate, is set to 0.001 and controls how quickly the Train method converges to a solution. Variable maxEpochs is set to 500 and limits how many times the weights and bias are updated in method Train.
The Train method uses the perceptron learning algorithm to search for and return the weights and bias values that create a perceptron that best fits the training data (in a sense I'll explain shortly). Method Accuracy uses the best weight and bias values to predict the class of each training item, compares each predicted class with the known class stored in the Y array, and calculates the percentage of correct classifications.
The demo program concludes by creating a new data item (1.0, 4.5) and using the perceptron to predict the item's class. Notice that there isn't a perceptron object of some sort. The perceptron consists of the weights and bias values plus method ComputeOutput. You may want to encapsulate my code into an explicit Perceptron class.
Computing Perceptron Output
Method ComputeOutput accepts three input arguments: a data item, the weights array and the bias value. The method returns either -1 or +1. It's possible to create multi-class (more than two class values) perceptrons rather than binary classification perceptrons, but in my opinion perceptrons are best suited for two-class problems.
Listing 2. Helper method Activation.
static int ComputeOutput(double[] data, double[] weights,
double bias)
{
double result = 0.0;
for (int j = 0; j < data.Length; ++j)
result += data[j] * weights[j];
result += bias;
return Activation(result);
}
static int Activation(double x)
{
if (x >= 0.0) return +1;
else return -1;
}
In Listing 2 I've defined a helper method, Activation, which is nothing more than a simple threshold function. In neural networks, activation functions can be much more complex. When using perceptrons for classification with real values, which can be positive or negative, it's usually best to code the two possible classes as -1 and +1 rather than 0 and 1.
The perceptron training method computes the error associated with the current weights and bias values. An obvious measure of error is the percentage of incorrectly classified training data items. However, error computation is surprisingly subtle and a different approach is used to compute a total error value.
Helper method Error computes how far away a perceptron's pre-activation output for a single training data item is from the item's actual class value; the Error method returns a value that's one-half of a sum of squared deviations:
static double Error(double[] data, double[] weights,
double bias, int Y)
{
double sum = 0.0;
for (int j = 0; j < data.Length; ++j)
sum += data[j] * weights[j];
sum += bias;
return 0.5 * (sum - Y) * (sum - Y);
}
Method TotalError is the sum of errors for all training data items:
static double TotalError(double[][] trainData, double[] weights,
double bias, int[] Y)
{
double totErr = 0.0;
for (int i = 0; i < trainData.Length; ++i)
totErr += Error(trainData[i], weights, bias, Y[i]);
return totErr;
}
Training the Perceptron
With methods ComputeOutput and TotalError defined, it's possible to define a training method that computes the best (lowest total error) weights and bias values for a given set of training data. Method Train is presented in Listing 3.
Listing 3. Training the perceptron.
static void Train(double[][] trainData, double alpha, int maxEpochs,
int[] Y, out double[] weights, out double bias)
{
int numWeights = trainData[0].Length;
double[] bestWeights = new double[numWeights]; // Best weights found, return value
weights = new double[numWeights]; // Working values (initially 0.0)
double bestBias = 0.0;
bias = 0.01; // Working value (initial small arbitrary value)
double bestError = double.MaxValue;
int epoch = 0;
while (epoch < maxEpochs)
{
for (int i = 0; i < trainData.Length; ++i) // Each input
{
int output = ComputeOutput(trainData[i], weights, bias);
int desired = Y[i]; // -1 or +1
if (output != desired) // Misclassification, so adjust weights and bias
{
double delta = desired - output; // How far off are you?
for (int j = 0; j < numWeights; ++j)
weights[j] = weights[j] + (alpha * delta * trainData[i][j]);
bias = bias + (alpha * delta);
// New best?
double totalError = TotalError(trainData, weights, bias, Y);
if (totalError < bestError)
{
bestError = totalError;
Array.Copy(weights, bestWeights, weights.Length);
bestBias = bias;
}
}
}
++epoch;
} // while
Array.Copy(bestWeights, weights, bestWeights.Length);
bias = bestBias;
return;
}
The training method is presented in high-level pseudo-code in Listing 4.
Listing 4. The perceptron training method in pseudo-code.
loop until done
foreach training data item
compute output using weights and bias
if the output is incorrect then
adjust weights and bias
compute error
if error < smallest error so far
smallest error so far = error
save new weights and bias
end if
end if
increment loop counter
end foreach
end loop
return best weights and bias values found
Although the training method doesn't have very many lines of code, it's quite clever. The heart of the method is the line that adjusts the weights when a training item is incorrectly classified:
weights[j] = weights[j] + (alpha * delta * trainData[i][j]);
The adjustment value has three terms: alpha, delta and the input value associated with the weight being adjusted. Delta is computed as desired - output, that is, the desired value stored in the Y array minus the output produced by the current weights and bias. Suppose that the desired value is +1 but the output value is -1. This means the output value is too small, and so weights and bias values must be adjusted to increase the output value. If the input associated with some weight is positive, then increasing the weight will increase the output. If the associated input is negative, then decreasing the weight will increase the output.
The learning rate, alpha, is typically some small value such as 0.001 or 0.00001, and throttles the magnitude of change when weights and bias values are adjusted. An advanced alternative is to allow alpha to change, starting out with a relatively large value and gradually decreasing. The idea is to have large adjustment jumps early on but then make the jumps finer-grained later. Another advanced alternative is to set alpha to a small random value each time it's used.
The version of the perceptron-training algorithm presented here iterates a fixed maxEpochs times (500 in the demo). Notice that no change to weights or bias will occur after all training data items are correctly classified. You might want to check for this condition and exit the main learning loop when it occurs.
The training algorithm computes the total error every time there's a change to weights and bias values. Because the total error function iterates through all training data items, this is an expensive process and may not be feasible for very large data sets. An alternative is to check total error only occasionally -- for instance, after every 10th change to the weights and bias.
Wrapping Up
Even though the training method uses a not-so-obvious measure of error to compute the weights and bias values that define a perceptron, ultimately what matters most is how well a perceptron classifies data. Method Accuracy, shown in Listing 5, returns the percentage of correctly classified data items.
Listing 5. Method Accuracy.
static double Accuracy(double[][] trainData, double[] weights,
double bias, int[] Y)
{
int numCorrect = 0;
int numWrong = 0;
for (int i = 0; i < trainData.Length; ++i)
{
int output = ComputeOutput(trainData[i], weights, bias);
if (output == Y[i]) ++numCorrect;
else ++numWrong;
}
return (numCorrect * 1.0) / (numCorrect + numWrong);
}
Finally, for the sake of completeness, here are the two display routines used in the demo program. Method ShowVector is:
static void ShowVector(double[] vector, int decimals)
{
for (int i = 0; i < vector.Length; ++i)
Console.Write(vector[i].ToString("F" + decimals) + " ");
Console.WriteLine("");
}
Method ShowTrainData is:
static void ShowTrainData(double[][] trainData, int[] Y)
{
for (int i = 0; i < trainData.Length; ++i)
{
Console.Write("[" + i.ToString().PadLeft(2, ' ') + "] ");
for (int j = 0; j < trainData[i].Length; ++j)
{
Console.Write(trainData[i][j].ToString("F1").PadLeft(6, ' '));
}
Console.WriteLine(" -> " + Y[i].ToString("+0;-0"));
}
}
The code and explanation presented in this article should give you a solid foundation for understanding classification with perceptrons. I recommend you investigate a bit with some of the alternatives I've suggested. Also, it's very informative to experiment by changing the value of the learning rate alpha, the value of the loop limit maxEpochs, the values of the training data and the values of an unknown data item to classify.
Perceptrons are just one of many machine-learning techniques that can be used to perform binary classification on real-valued input. The key weakness of perceptrons is that they only work well on data that can be linearly separated. In Figure 2, notice that it's possible to separate the two classes of data items using a straight line. In other words, there are some types of binary classification problems where perceptrons just don't work. This weakness led to the creation of neural networks, which are collections of interconnected perceptrons.