Neural Network Lab
How To Standardize Data for Neural Networks
Understanding data encoding and normalization is an absolutely essential skill when working with neural networks. James McCaffrey walks you through what you need to know to get started.
Dealing with neural network data can be somewhat tricky. Suppose you want to create a neural network that will predict a person's political party affiliation (Democrat, Republican, Independent or other) based on the person's age, sex (male or female), annual income and location type (urban, suburban or rural). For example, the first line of your training data might look like:
30 male 38000.00 urban democrat
Because neural networks natively process numeric data, the sex, location type and political affiliation data must be encoded to numeric values. For example, one possibility for sex is to encode male as 0 and female as 1. In addition to the necessity of encoding categorical data, experience has shown that neural network training is usually more efficient when numeric x-data (age and annual income, in this example) are scaled, or normalized, so that their magnitudes are relatively similar.
The process of encoding categorical data and normalizing numeric data is sometimes called data standardization. Although data standardization is not a glamorous topic, understanding data encoding and normalization is an absolutely essential skill when working with neural networks.
The demo program (download above) is coded using C#, but you should be able to refactor the demo to another language, such as JavaScript or Python, without too much difficulty. Most normal error-checking code has been removed to keep the size of the demo small and the main ideas clear.
The best way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1.
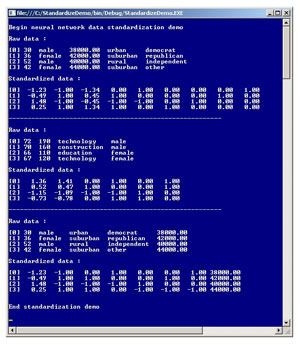 [Click on image for larger view.]
Figure 1. Standardizing Neural Network Data.
[Click on image for larger view.]
Figure 1. Standardizing Neural Network Data.
The demo program has three short examples of data standardization. In the first mini-example, the demo sets up four lines of raw data:
[0] 30 male 38000.00 urban democrat
[1] 36 female 42000.00 suburban republican
[2] 52 male 40000.00 rural independent
[3] 42 female 44000.00 suburban other
The demo assumes that the y-data to be predicted is in the last column of the data. Behind the scenes, a data standardization object is created and used to standardize the raw data. The result, with some parentheses added to make the output easier to read, is:
[0] -1.23 -1.0 -1.34 ( 0.0 1.0) (0.0 0.0 0.0 1.0)
[1] -0.49 1.0 0.45 ( 1.0 0.0) (0.0 0.0 1.0 0.0)
[2] 1.48 -1.0 -0.45 (-1.0 -1.0) (0.0 1.0 0.0 0.0)
[3] 0.25 1.0 1.34 ( 1.0 0.0) (1.0 0.0 0.0 0.0)
For the first line of raw data, the age of 30 has been normalized to -1.23, and the annual income of $38,000.00 has been normalized to -1.34. For all data, sex has been encoded so that male = -1 and female = +1. The location type has been encoded using what is called 1-of-(C-1) effects-coding. Here, urban = (0 1), suburban = (1 0), and rural = (-1 -1). The y-data to be predicted (also called the dependent data), political party affiliation, has been encoded using what is called 1-of-C dummy-coding: Democrat = (0 0 0 1), Republican = (0 0 1 0), Independent = (0 1 0 0), and other = (1 0 0 0).
Normalizing Numeric Data
In theory, it's not necessary to normalize numeric x-data (also called independent data). However, practice has shown that when numeric x-data values are normalized, neural network training is often more efficient, which leads to a better predictor. Basically, if numeric data is not normalized, and the magnitudes of two predictors are far apart, then a change in the value of a neural network weight has far more relative influence on the x-value with larger magnitudes. For example, for the first line of raw data, a neural network weight change of 0.1 will change magnitude of the age factor by (0.1 * 30) = 3, but will change the income factor by (0.1 * 38,000) = 3,800.
The demo program normalizes numeric data by computing, for each numeric x-data column value v, v' = (v - mean) / std dev. This technique is sometimes called Gaussian normalization. For example, the mean of the age column = (30 + 36 + 52 + 42) / 4 = 160 / 4 = 40.0. The standard deviation of the age column = sqrt((30-40)^2 + (36-40)^2 + (52-40)^2 + (42-40)^2) / 4) = sqrt((100 + 16 + 144 + 4) / 4) = sqrt(66.0) = 8.12. So the normalized value for an age of 30 = (30 - 40.0) / 8.12 = -1.23, as shown in Figure 1 earlier in this article.
Gaussian normalization typically leads to normalized x-values that are all generally between -10 and +10. There are several alternatives to Gaussian normalization. The most common alternative is a technique called Min-Max normalization.
In general, there's no need to normalize numeric y-data, except in unusual situations. Prediction problems where the y-data is numeric are called regression problems, as opposed to problems where the y-data is categorical, which are called classification problems. In the third mini-example in Figure 1, the data from the first example are rearranged so that the problem is to predict a person's annual income based on their age, sex, location and political party affiliation. You can see that that in the standardized version of the data, the numeric y-data hasn't been modified.
Encoding Categorical X-Data
When dealing with categorical x-data, it's useful to distinguish between binary x-data, such as sex, which can take one of two possible values, and regular categorical data, such as location, which can take one of three or more possible values. Experience has shown that it's better to encode binary x-data using a -1, +1 scheme rather than a 0, 1 scheme.
For regular categorical x-data, the demo program uses 1-of-(C-1) effects-coding, which is best explained by example. Suppose, as in Figure 1, you have an x-variable, location, which can take on one of three categorical values: urban, suburban or rural. With effects-coding for n categorical values, the first n-1 values are encoded with n-1 bits, using 0s and a single 1: urban = (0 1), suburban = (1 0). You'd expect the last value, rural, to be encoded as (0 0) or (1 1). However, again, practice has shown that it's better to code the last categorical value using n-1 -1 values: (-1 -1).
There's one exception to the rule of thumb to encode categorical x-data using 1-of-(C-1) effects-coding. If you intend to train your neural network using a technique called weight decay, it's preferable to encode categorical x-data using 1-of-C dummy-coding (explained in the next section).
Encoding Categorical Y-Data
When dealing with categorical y-data, just as with categorical x-data, it's useful to distinguish between binary y-data and regular categorical y-data. Scenarios with binary y-data, such as predicting a person's sex, can be handled in two equivalent ways. One way is to use 1-of-(C-1) dummy-coding in conjunction with the logistic sigmoid output layer activation. For example, for sex, you'd use a single variable, where 0 represents male and 1 represents female. Because logistic sigmoid generates a single value between 0 and 1, you can interpret values between 0 and 0.5 as indicating male and values between 0.5 and 1 as indicating female.
The other approach for binary y-data, and the one I prefer, is 1-of-C dummy-coding in conjunction with the softmax output layer activation. For example, for sex, (0 1) indicates male and (1 0) indicates female. A typical softmax output might be (0.33 0.67) where the first value can loosely be interpreted as the probability of male and the second value as the probability of female.
Regular categorical y-data, with three or more possible values, should be encoded using 1-of-C dummy-coding. For example, if there are four possible y-values -- Democrat, Republican, Independent, other -- then Democrat = (0 0 0 1), Republican = (0 0 1 0), Independent = (0 1 0 0) and other = (1 0 0 0).
Data encoding and normalization is summarized in the table in Figure 2. For numeric x-data, I prefer Gaussian normalization over Min-Max normalization. For binary y-data, I prefer 1-of-C dummy-coding over the equivalent, but more commonly used, 1-of-(C-1) dummy-coding technique.
Figure 2: Data Encoding and Normalization Summary
| Neural Network Data Type |
Standardization Technique |
|
|
| Numeric x-data |
Gaussian normalization or Min-Max normalization |
| Binary x-data |
-1, +1 encoding |
| Categorical x-data (no weight decay) |
1-of-(C-1) effects-coding |
| Categorical x-data (with weight decay) |
1-of-C dummy-coding |
|
|
| Numeric y-data |
No normalization |
| Binary y-data |
1-of-(C-1) dummy-coding with log sigmoid activation, or 1-of-C dummy-coding with softmax activation |
| Categorical y-data |
1-of-C dummy-coding with softmax activation |
|
Overall Program Structure
To create the demo program, I launched Visual Studio and created a new C# console application program named StandardizeDemo. After the template code loaded, I removed all using statements except those to the System and System.Collections.Generic namespaces. In the Solution Explorer window, I renamed file Program.cs to the more-descriptive StandardizeProgram.cs, and VS automatically renamed class Program for me.
The overall program structure, with some minor edits to save space, is shown in Listing 1.
Listing 1: Standardization Demo Program Structure
using System;
using System.Collections.Generic;
namespace StandardizeDemo
{
class StandardizeProgram
{
static void Main(string[] args)
{
Console.WriteLine("Begin standardization demo");
// age, sex, income, location -> politics
string[][] rawData = new string[4][];
rawData[0] = new string[] { "30", "male ", "38000.00",
"urban ", "democrat " };
rawData[1] = new string[] { "36", "female", "42000.00",
"suburban", "republican" };
rawData[2] = new string[] { "52", "male ", "40000.00",
"rural ", "independent" };
rawData[3] = new string[] { "42", "female", "44000.00",
"suburban", "other " };
Console.WriteLine("Raw data :");
Helpers.ShowMatrix(rawData, true, true);
string[] colTypes = new string[] { "numeric", "categorical",
"numeric", "categorical", "categorical" };
Standardizer s = new Standardizer(rawData, colTypes);
double[][] standardData = s.StandardizeAll(rawData);
Console.WriteLine("Standardized data :");
Helpers.ShowMatrix(standardData, 2, true, true);
// height, weight, occupation -> sex
rawData[0] = new string[] { "72", "190", "technology ",
"male " };
rawData[1] = new string[] { "70", "160", "construction",
"male " };
rawData[2] = new string[] { "66", "110", "education ",
"female" };
rawData[3] = new string[] { "67", "120", "technology ",
"female" };
Console.WriteLine("-----------------------------------");
Console.WriteLine("Raw data :");
Helpers.ShowMatrix(rawData, true, true);
colTypes = new string[] { "numeric", "numeric", "categorical",
"categorical" };
s = new Standardizer(rawData, colTypes);
standardData = s.StandardizeAll(rawData);
Console.WriteLine("Standardized data :");
Helpers.ShowMatrix(standardData, 2, true, true);
// age, sex, location, politics -> income
rawData[0] = new string[] { "30", "male ", "urban ",
"democrat ", "38000.00" };
rawData[1] = new string[] { "36", "female", "suburban",
"republican ", "42000.00" };
rawData[2] = new string[] { "52", "male ", "rural ",
"independent", "40000.00" };
rawData[3] = new string[] { "42", "female", "suburban",
"other ", "44000.00" };
Console.WriteLine("-----------------------------------");
Console.WriteLine("Raw data :");
Helpers.ShowMatrix(rawData, true, true);
colTypes = new string[] { "numeric", "categorical",
"categorical", "categorical", "numeric" };
s = new Standardizer(rawData, colTypes);
standardData = s.StandardizeAll(rawData);
Console.WriteLine("Standardized data : \n");
Helpers.ShowMatrix(standardData, 2, true, true);
Console.WriteLine("End standardization demo");
Console.ReadLine();
} // Main
} // Program
public class Standardizer
{
public string[] colTypes;
public string[] subTypes;
public string[][] distinctValues;
public double[] means;
public double[] stdDevs;
public int numStandardCols;
public Standardizer(string[][] rawData, string[] colTypes) { . . }
public double[] GetStandardRow(string[] tuple) { . . }
private int IndexOf(int col, string catValue) { . . }
public double[][] StandardizeAll(string[][] rawData) { . . }
}
public class Helpers
{
public static void ShowMatrix(string[][] matrix,
bool indices, bool newLine) { . . }
public static void ShowMatrix(double[][] matrix,
int decimals, bool indices, bool newLine) { . . }
public static void ShowVector(double[] vector, int decimals,
bool newLine) { . . }
}
}
The demo program begins by setting up some raw data. I padded categorical values with blank spaces just so the data would display nicely. In realistic scenarios, your raw data would likely come from a text file orSQL table.
An important assumption I've made here is that the y-data to be predicted is in the last column.
// age, sex, income, location -> politics
string[][] rawData = new string[4][];
rawData[0] = new string[] { "30", "male ", "38000.00",
"urban ", "democrat " };
// etc.
The Standardizer object is instantiated like so:
string[] colTypes = new string[] { "numeric", "categorical",
"numeric", "categorical", "categorical" };
Standardizer s = new Standardizer(rawData, colTypes);
double[][] standardData = s.StandardizeAll(rawData);
The constructor accepts the raw data to be standardized, and an array that tells the constructor whether each column is numeric or categorical. An alternative is to modify the code presented in this article so that the constructor automatically infers the type of each column. This is a bit trickier than you might expect. The constructor scans through the raw data and extracts all the information necessary, such as the means and standard deviations of the numeric columns, and the distinct values in each categorical column, to standardize the data.
Class Standardizer exposes two public methods. Method StandardizeAll accepts a matrix of raw string data and returns a standardized matrix of double. Method GetStandardRow accepts a single row of raw data and returns its standardized equivalent.
The Standardizer Class
The Standardizer class has five data members, all declared with public scope for simplicity:
public string[] colTypes;
public string[] subTypes;
public string[][] distinctValues;
public double[] means;
public double[] stdDevs;
public int numStandardCols;
Array colTypes holds string values "numeric" or "categorical." Using strings in this way is rather error-prone and inefficient, so you might want to consider refactoring my code to use an Enumeration type instead. Array subTypes holds values "numeric," "numericY," "binaryX," "binaryY," "categoricalX" and "categoricalY." These values are computed by the constructor. For example, if a column is "numeric" and the last column, its subtype is ""numericY." If a column is "categorical," has two distinct values and is not the last column, its subtype is "binaryX".
Listing 2: Standardizer Class Constructor
public Standardizer(string[][] rawData, string[] colTypes)
{
this.colTypes = new string[colTypes.Length];
Array.Copy(colTypes, this.colTypes, colTypes.Length);
// get distinct values in each col.
int numCols = rawData[0].Length;
this.distinctValues = new string[numCols][];
for (int j = 0; j < numCols; ++j)
{
if (colTypes[j] == "numeric")
{
distinctValues[j] = new string[] { "na" };
}
else
{
Dictionary<string, bool> values =
new Dictionary<string, bool>();
for (int i = 0; i < rawData.Length; ++i)
{
string v = rawData[i][j];
if (values.ContainsKey(v) == false)
values.Add(v, true);
}
distinctValues[j] = new string[values.Count];
int k = 0;
foreach (string s in values.Keys)
{
distinctValues[j][k] = s;
++k;
}
}
}
// compute means of numeric cols
this.means = new double[numCols];
for (int j = 0; j < numCols; ++j)
{
if (colTypes[j] == "categorical")
{
this.means[j] = -1.0; // dummy values
}
else
{
double sum = 0.0;
for (int i = 0; i < rawData.Length; ++i)
{
double v = double.Parse(rawData[i][j]);
sum += v;
}
this.means[j] = sum / rawData.Length;
}
}
// compute standard deviations of numeric cols
this.stdDevs = new double[numCols];
for (int j = 0; j < numCols; ++j)
{
if (colTypes[j] == "categorical")
{
this.stdDevs[j] = -1.0; // dummy
}
else
{
double ssd = 0.0; // sum of squared deviations
for (int i = 0; i < rawData.Length; ++i)
{
double v = double.Parse(rawData[i][j]);
ssd += (v - this.means[j]) * (v - this.means[j]);
}
this.stdDevs[j] = Math.Sqrt(ssd / rawData.Length);
}
}
// compute column subTypes
this.subTypes = new string[numCols];
for (int j = 0; j < numCols; ++j)
{
if (colTypes[j] == "numeric" && j != numCols - 1)
this.subTypes[j] = "numericX";
else if (colTypes[j] == "numeric" && j == numCols - 1)
this.subTypes[j] = "numericY";
else if (colTypes[j] == "categorical" && j != numCols - 1 &&
distinctValues[j].Length == 2)
this.subTypes[j] = "binaryX";
else if (colTypes[j] == "categorical" && j == numCols - 1 &&
distinctValues[j].Length == 2)
this.subTypes[j] = "binaryY";
else if (colTypes[j] == "categorical" && j != numCols - 1 &&
distinctValues[j].Length >= 3)
this.subTypes[j] = "categoricalX";
else if (colTypes[j] == "categorical" && j == numCols - 1 &&
distinctValues[j].Length >= 3)
this.subTypes[j] = "categoricalY";
}
// compute number of columns of standardized data
int ct = 0;
for (int j = 0; j < numCols; ++j)
{
if (this.subTypes[j] == "numericX")
++ct;
else if (this.subTypes[j] == "numericY")
++ct;
else if (this.subTypes[j] == "binaryX")
++ct;
else if (this.subTypes[j] == "binaryY")
ct += 2;
else if (this.subTypes[j] == "categoricalX")
ct += distinctValues[j].Length - 1;
else if (this.subTypes[j] == "categoricalY")
ct += distinctValues[j].Length;
}
this.numStandardCols = ct;
}
Matrix distinctValues holds distinct values for each categorical column. This gives the class the ability to determine how many columns there will be in the standardized result. Arrays means and stdDevs hold the means and standard deviations of numeric columns so numeric columns can be Gaussian normalized. Member numStandardCols is the number of columns in the standardized output. For example, in Figure 1, the raw data in the first demo has five columns but the standardized result has nine columns, because categorical data can generate multiple columns.
The Standardizer constructor is a bit long because I didn't use any helper methods. The constructor code is presented in Listing 2.
In pseudo-code, the constructor works like this:
loop each column of raw data
if column is categorical
if curr value has not been seen
save it in distinctValues
end if
end if
if column is numeric
compute mean of column
use mean to compute std dev of column
end if
end loop
compute column subtypes
compute numStandardCols
The algorithm to determine the number of output columns is:
ct = 0
loop each column
if col is numeric x-data
++ct // Gaussian
else if col is numeric y-data
++ct // no normalization
else if col is binary x-data
++ct // -1, +1
else if col is binary y-data
ct += 2 // 1-of-C dummy
else if col is categorical x-data
ct += num distinct values - 1 // 1-of-(C-1) effects
else if col is categorical y-data
ct += num distinct values // 1-of-C dummy
end if
end loop
Methods StandardizeAll and GetStandardRow
The Standardizer class constructor scans its raw data and collects the information needed to standardize the data. Method GetStandardRow uses that information to process a single row of raw data. The method definition begins:
public double[] GetStandardRow(string[] tuple)
{
double[] result = new double[this.numStandardCols];
int p = 0; // ptr into result data
. . .
Recall that the constructor has determined how many columns there will be in an output row and stored that information into numStandardCols. Next, the method iterates through each column of the input data:
for (int j = 0; j < tuple.Length; ++j)
{
if (this.subTypes[j] == "numericX")
{
double v = double.Parse(tuple[j]);
result[p++] = (v - this.means[j]) / this.stdDevs[j];
}
else if (this.subTypes[j] == "numericY")
{
double v = double.Parse(tuple[j]);
result[p++] = v; // leave alone (regression problem)
}
. . .
After dealing with numeric data, method GetStandardRow handles binary data:
else if (this.subTypes[j] == "binaryX")
{
string v = tuple[j];
int index = IndexOf(j, v);
if (index == 0)
result[p++] = -1.0;
else
result[p++] = 1.0;
}
else if (this.subTypes[j] == "binaryY")
{
string v = tuple[j];
int index = IndexOf(j, v);
if (index == 0) { result[p++] = 0.0; result[p++] = 1.0; }
else { result[p++] = 1.0; result[p++] = 0.0; }
}
. . .
Helper method IndexOf returns the 0-based index of a categorical data item. For example, if a column has two values, male and female, then IndexOf(male) = 0 and IndexOf(female) = 1. Method IndexOf is defined:
private int IndexOf(int col, string catValue)
{
for (int k = 0; k < this.distinctValues[col].Length; ++k)
if (distinctValues[col][k] == catValue)
return k;
return -1; // fatal error
}
Method IndexOf does a simple linear scan of the distinctValues array. You might want to consider creating lookup tables for each column instead.
Next, method GetStandardRow handles categorical x-data:
else if (this.subTypes[j] == "categoricalX")
{
string v = tuple[j];
int ct = distinctValues[j].Length;
double[] tmp = new double[ct-1];
int index = IndexOf(j, v);
if (index == ct - 1) {
for (int k = 0; k < tmp.Length; ++k)
tmp[k] = -1.0;
}
else {
for (int k = 0; k < tmp.Length; ++k)
tmp[k] = 0.0; // not necessary in C# . .
tmp[ct - index - 2] = 1.0;
}
for (int k = 0; k < tmp.Length; ++k)
result[p++] = tmp[k];
}
. . .
This code implements 1-of-(C-1) effects-coding and is a bit tricky. Method GetStandardRow finishes by using 1-of-C dummy-coding to deal with categorical y-data:
. . .
else if (this.subTypes[j] == "categoricalY")
{
string v = tuple[j];
int ct = distinctValues[j].Length;
double[] tmp = new double[ct];
int index = IndexOf(j, v);
for (int k = 0; k < tmp.Length; ++k)
tmp[k] = 0.0; // not necessary in C# . .
tmp[ct - index - 1] = 1.0;
for (int k = 0; k < tmp.Length; ++k)
result[p++] = tmp[k];
}
} // each j col
return result;
}
The Standardizer class implements method StandardizeAll as a wrapper around method GetStandardRow:
public double[][] StandardizeAll(string[][] rawData)
{
double[][] result = new double[rawData.Length][];
for (int i = 0; i < rawData.Length; ++i)
{
double[] stdRow = this.GetStandardRow(rawData[i]);
result[i] = stdRow;
}
return result;
}
Modifications and Extensions
The code and explanations presented in this article should get you up and running with data standardization for neural networks. The Standardizer class presented here is not parameterized. You might want to extend my code so that the constructor accepts arguments for options such as normalization algorithm (Gaussian or Min-Max), and encoding algorithm for categorical x-data -- (1-of-(C-1) effects-coding or 1-of-C dummy-coding when weight decay will be used during training.
The code presented here assumes the y-data is in the last column of the raw data. Instead, you might want to pass an int parameter to the constructor that indicates where the y-data is.